Hostname: page-component-7dd5485656-7jgsp Total loading time: 0 Render date: 2025-10-30T22:50:03.468Z Has data issue: false hasContentIssue false
  • English
  • Français

Données endoscopiques d’un groupe réductif connexe : applications d’une construction de Langlands

Part of: Lie groups

Published online by Cambridge University Press:  15 May 2020

Bertrand Lemaire  and
Jean-Loup Waldspurger
Bertrand Lemaire
Affiliation:
CNRS, Institut de Mathématiques de Marseille (UMR 7373), Campus de Luminy, Case Postale 907, F–13288 Marseille Cedex 9, France e-mail: bertrand.lemaire@univ-amu.fr
Jean-Loup Waldspurger
Affiliation:
CNRS, Institut de Mathématiques de Jussieu-Paris-Rive-Gauche, 2 place Jussieu, 75005 Paris, France e-mail: jean-loup.waldspurger@imj-prg.fr
Get access Rights & Permissions [Opens in a new window]

Résumé

Soient 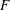$F$ un corps global, et 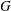$G$ un groupe réductif connexe défini sur 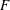$F$. On prouve que si deux données endoscopiques de 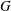$G$ sont équivalentes en presque toute place de 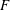$F$, alors elles sont équivalentes. Le résultat est encore vrai pour l’endoscopie (ordinaire) avec caractère. On donne aussi, pour 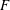$F$ global ou local et 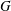$G$ quasi-simple simplement connexe, une description des données endoscopiques elliptiques de 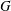$G$.

Abstract

Abstract

Let 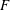$F$ be a global field, and 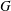$G$ a connected reductive group defined over 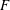$F$. We prove that two endoscopic data of 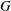$G$ which are equivalent almost everywhere, are equivalent. The result remains true for (non-twisted) endoscopy with character. We also give, for 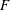$F$ global or local and 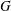$G$ quasi-simple simply connected, a description of the elliptic endoscopic data of 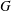$G$.

Keywords

endoscopie ordinairedonnée endoscopique elliptiquelocalisation

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields
Secondary: 22E55: Representations of Lie and linear algebraic groups over global fields and adèle rings

Information

Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 4 , August 2021 , pp. 1074 - 1094
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bibliographie

Borel, A., Automorphic L-functions . Proc. Symp. Pure Math. 33(1979), part 2, 27–61.CrossRefGoogle Scholar
Borel, A. and Tits, J., Groupes réductifs. Publ. Math. Inst. Hautes Études Scientifiques 27(1965), 55–150.CrossRefGoogle Scholar
Bourbaki, N., Groupes et algèbres de Lie, chapitres 4, 5 et 6. Hermann, 1968.Google Scholar
Labesse, J.-P. and Lapid, E., Characters of G over local and global fields, appendice à Lapid E., Mao Z., A conjecture of Whittaker–Fourier coefficients of cusp forms. J. Number Theory 146(2015), 448–505.Google Scholar
Langlands, R., Stable conjugacy: definitions and lemmas. Canad. J. Math. 31(1979), 700–725.CrossRefGoogle Scholar
Mœglin, C. and Waldspurger, J.-L., Stabilisation de la formule des traces tordue, vol. 1 et 2. Progress in Math., Birkhäuser 316–317(2016).CrossRefGoogle Scholar
Waldspurger, J.-L., Caractères automorphes d’un groupe réductif. Prépublication (2016). arxiv:1608.07150Google Scholar