Let 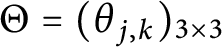 $\Theta =(\theta _{j,k})_{3\times 3}$ be a nondegenerate real skew-symmetric
$\Theta =(\theta _{j,k})_{3\times 3}$ be a nondegenerate real skew-symmetric  $3\times 3$ matrix, where
$3\times 3$ matrix, where 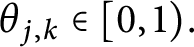 $\theta _{j,k}\in [0,1).$ For any
$\theta _{j,k}\in [0,1).$ For any 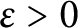 $\varepsilon>0$, we prove that there exists
$\varepsilon>0$, we prove that there exists 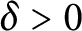 $\delta>0$ satisfying the following: if
$\delta>0$ satisfying the following: if 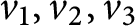 $v_1,v_2,v_3$ are three unitaries in any unital simple separable
$v_1,v_2,v_3$ are three unitaries in any unital simple separable 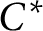 $C^*$-algebra A with tracial rank at most one, such that
$C^*$-algebra A with tracial rank at most one, such that $$\begin{align*}\|v_kv_j-e^{2\pi i \theta_{j,k}}v_jv_k\|<\delta \,\,\,\, \mbox{and}\,\,\,\, \frac{1}{2\pi i}\tau(\log_{\theta}(v_kv_jv_k^*v_j^*))=\theta_{j,k}\end{align*}$$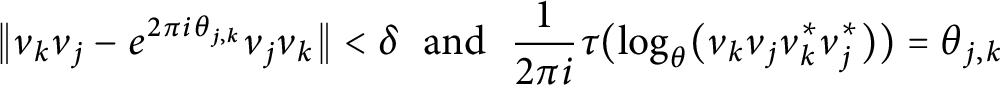
for all 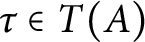 $\tau \in T(A)$ and
$\tau \in T(A)$ and 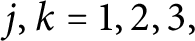 $j,k=1,2,3,$ where
$j,k=1,2,3,$ where 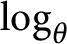 $\log _{\theta }$ is a continuous branch of logarithm (see Definition 4.13) for some real number
$\log _{\theta }$ is a continuous branch of logarithm (see Definition 4.13) for some real number 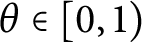 $\theta \in [0, 1)$, then there exists a triple of unitaries
$\theta \in [0, 1)$, then there exists a triple of unitaries 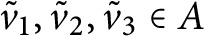 $\tilde {v}_1,\tilde {v}_2,\tilde {v}_3\in A$ such that
$\tilde {v}_1,\tilde {v}_2,\tilde {v}_3\in A$ such that $$\begin{align*}\tilde{v}_k\tilde{v}_j=e^{2\pi i\theta_{j,k} }\tilde{v}_j\tilde{v}_k\,\,\,\,\mbox{and}\,\,\,\,\|\tilde{v}_j-v_j\|<\varepsilon,\,\,j,k=1,2,3.\end{align*}$$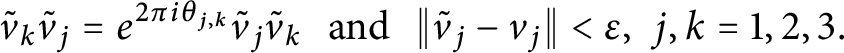
The same conclusion holds if  $\Theta $ is rational or nondegenerate and A is a nuclear purely infinite simple
$\Theta $ is rational or nondegenerate and A is a nuclear purely infinite simple 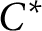 $C^*$-algebra (where the trace condition is vacuous).
$C^*$-algebra (where the trace condition is vacuous).
If  $\Theta $ is degenerate and A has tracial rank at most one or is nuclear purely infinite simple, we provide some additional injectivity conditions to get the above conclusion.
$\Theta $ is degenerate and A has tracial rank at most one or is nuclear purely infinite simple, we provide some additional injectivity conditions to get the above conclusion.
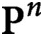 $\textbf{P}^n$ with vanishing lower cohomologies
$\textbf{P}^n$ with vanishing lower cohomologies
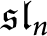 $\mathfrak {sl}_n$
$\mathfrak {sl}_n$
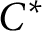 $C^*$-algebras
$C^*$-algebras