Hostname: page-component-cb9f654ff-plnhv Total loading time: 0.001 Render date: 2025-08-22T19:48:51.174Z Has data issue: false hasContentIssue false
  • English
  • Français

Steiner symmetry in the minimization of the first eigenvalue of a fractional eigenvalue problem with indefinite weight

Part of: Variational methods for eigenvalues of operators General theory of linear operators Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  14 April 2020

Claudia Anedda ,
Fabrizio Cuccu  and
Silvia Frassu
Claudia Anedda
Affiliation:
Department of Mathematics and Computer Science, University of Cagliari, via Ospedale 72, 09124 Cagliari, Italy e-mail: canedda@unica.it silvia.frassu@unica.it
Fabrizio Cuccu*
Affiliation:
Department of Mathematics and Computer Science, University of Cagliari, via Ospedale 72, 09124 Cagliari, Italy e-mail: canedda@unica.it silvia.frassu@unica.it
Silvia Frassu
Affiliation:
Department of Mathematics and Computer Science, University of Cagliari, via Ospedale 72, 09124 Cagliari, Italy e-mail: canedda@unica.it silvia.frassu@unica.it
*
e-mail: fcuccu@unica.it
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 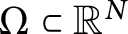$\Omega \subset \mathbb {R}^N$, 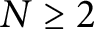$N\geq 2$, be an open bounded connected set. We consider the fractional weighted eigenvalue problem 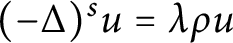$(-\Delta )^s u =\lambda \rho u$ in $\Omega $ with homogeneous Dirichlet boundary condition, where 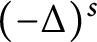$(-\Delta )^s$, 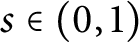$s\in (0,1)$, is the fractional Laplacian operator, 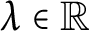$\lambda \in \mathbb {R}$ and 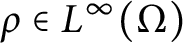$ \rho \in L^\infty (\Omega )$.

We study weak* continuity, convexity and Gâteaux differentiability of the map 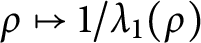$\rho \mapsto 1/\lambda _1(\rho )$, where 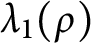$\lambda _1(\rho )$ is the first positive eigenvalue. Moreover, denoting by 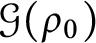$\mathcal {G}(\rho _0)$ the class of rearrangements of 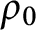$\rho _0$, we prove the existence of a minimizer of 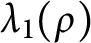$\lambda _1(\rho )$ when 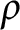$\rho $ varies on 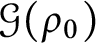$\mathcal {G}(\rho _0)$. Finally, we show that, if $\Omega $ is Steiner symmetric, then every minimizer shares the same symmetry.

Keywords

Fractional Laplacianeigenvalue problemoptimizationSteiner symmetry

MSC classification

Primary: 35R11: Fractional partial differential equations
Secondary: 47A75: Eigenvalue problems 49R05: Variational methods for eigenvalues of operators (should also be assigned at least one other classification number in Section 49)

Information

Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 4 , August 2021 , pp. 970 - 992
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alvino, A., Trombetti, G. and Lions, P.L., On optimization problems with prescribed rearrangements. Nonlinear Anal. 13(1989), no. 2, 185–220. https://doi.org/10.1016/0362-546x(89)90043-6 CrossRefGoogle Scholar
Anedda, C. and Cuccu, F., Steiner symmetry in the minimization of the first eigenvalue in problems involving the p-Laplacian. Proc. Amer. Math. Soc. 144(2016), 3431–3440. https://doi.org/10.1090/proc/12972 CrossRefGoogle Scholar
Anedda, C. and Cuccu, F., Symmetry breaking in the minimization of the second eigenvalue for composite membranes. Proc. Roy. Soc. Edinburgh Sect. A 145(2015), 1–11. https://doi.org/10.1017/s030821051300098x CrossRefGoogle Scholar
Baernstein, A. II, A unified approach to symmetrization. Sympos. Math., vol. XXXV, Cambridge Univ. Press, Cambridge (1994), 47–91.Google Scholar
Berestycki, H., Le nombre de solutions de certains problèmes semi-linéaires elliptiques. J. Funct. Anal. 40(1981), 1–29. https://doi.org/10.1016/0022-1236(81)90069-0 CrossRefGoogle Scholar
Berestycki, H., Roquejoffre, J.-M. and Rossi, L., The periodic patch model for population dynamics with fractional diffusion. Discrete Contin. Dyn. Syst. Ser. S 4(1)(2011), 1–13. https://doi.org/10.3934/dcdss.2011.4.1 Google Scholar
Brezis, H., Functional analysis, Sobolev spaces and partial differential equations. Springer, New York (2011).CrossRefGoogle Scholar
Brock, F., Rearrangements and applications to symmetry problems in PDE. In: Handbook of differential equations, stationary partial differential equations, 4, Elsevier (2007), 1–60. https://doi.org/10.1016/s1874-5733(07)80004-0 Google Scholar
Bucur, C. and Valdinoci, E., Nonlocal diffusion and applications, 20. Springer, Bologna (2016).CrossRefGoogle Scholar
Burton, G.R., Rearrangements of functions, maximization of convex functionals and vortex rings . Math. Ann. 276(1987), 225–253. https://doi.org/10.1007/bf01450739 CrossRefGoogle Scholar
Burton, G.R., Variational problems on classes of rearrangements and multiple configurations for steady vortices . Ann. Inst. H. Poincaré Anal. Non Linéaire 6(1989), no. 4, 295–319. https://doi.org/10.1016/S0294-1449(16)30320-1 CrossRefGoogle Scholar
Cabré, X. and Sire, Y., Nonlinear equations for fractional Laplacians I: Regularity, maximum principles, and Hamiltonian estimates. Ann. Inst. Henri Poincaré (C) Nonlinear Analysis 31(2014), 23–53. https://doi.org/10.1016/j.anihpc.2013.02.001 CrossRefGoogle Scholar
Caffarelli, L., Nonlocal diffusions, drifts and games. In: Nonlinear partial differential equations, Springer, Berlin Heidelberg (2012), 37–52. https://doi.org/10.1007/978-3-642-25361-4_3 Google Scholar
Cantrell, R.S. and Cosner, C., Diffusive logistic equations with indefinite weights: population models in disrupted environments. Proc. R. Soc. Edinb. Sect A 112, 3-4(1989), 293–318. https://doi.org/10.1017/s030821050001876x CrossRefGoogle Scholar
Cosner, C., Cuccu, F. and Porru, G., Optimization of the first eigenvalue of equations with indefinite weights . Adv. Nonlinear. Stud. 13(2013), 79–95. https://doi.org/10.1515/ans-2013-0105 CrossRefGoogle Scholar
Cox, S.J. and McLaughlin, J.R., Extremal eigenvalue problems for composite membranes, I. Appl. Math. Optim. 22(1990), 153–167. https://doi.org/10.1007/bf01447325 CrossRefGoogle Scholar
Cox, S.J. and McLaughlin, J.R., Extremal eigenvalue problems for composite membranes, II. Appl. Math. Optim. 22(1990), 169–187. https://doi.org/10.1007/bf01447326 CrossRefGoogle Scholar
Day, P. W., Rearrangements of measurable functions. Ph.D. dissertation, California Institute of Technology (1970).Google Scholar
de Figueiredo, D.G., Positive solutions of semilinear elliptic problems. In: Dold, A. and Eckmann, B. (eds.), Differential equations, Lecture Notes in Mathematics 957, Springer, Berlin (1982), 34–87. https://doi.org/10.1007/BFb0066233 Google Scholar
Di Nezza, E., Palatucci, G. and Valdinoci, E., Hitchhiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math. 136(2012), 521–573. https://doi.org/10.1016/j.bulsci.2011.12.004 CrossRefGoogle Scholar
Ekeland, I. and Témam, R., Convex analysis and variational problems. Classics in Applied Mathematics 28, SIAM (1999).CrossRefGoogle Scholar
Frassu, S. and Iannizzotto, A., Strict monotonicity and unique continuation for general non-local eigenvalue problems. Taiwanese J. Math. Advance Publication 24(2020), 681–694. https://doi.org/10.11650/tjm/190709 Google Scholar
Hardy, G. H., Littlewood, J. E. and Pólya, G., Inequalities. 2nd ed., Cambridge University Press, Cambridge(1952, first published in 1934).Google Scholar
Henrot, A., Extremum problems for eigenvalues of elliptic operators. Frontiers in Mathematics, Birkhuser Verlag, Basel (2006).CrossRefGoogle Scholar
Iannizzotto, A. and Papageorgiou, N. S., Existence and multiplicity results for resonant fractional boundary value problems. Discrete Contin. Dyn. Syst. Ser. S 11(2018), 511–532. https://doi.org/10.3934/dcdss.2018028 Google Scholar
Kawhol, B., Rearrangements and convexity of level sets in PDE. Lecture Notes in Mathematics, 1150, Springer, Berlin (1985).CrossRefGoogle Scholar
Lax, P.D., Functional analysis. Wiley, New York (2002).Google Scholar
Bisci, G. Molica, Radulescu, V.D. and Servadei, R., Variational methods for nonlocal fractional problems, 162. Cambridge University Press, Cambridge, UK (2016). https://doi.org/10.1017/cbo9781316282397 CrossRefGoogle Scholar
Olivares Contador, F., The Faber-Krahn inequality for the first eigenvalue of the fractional Dirichlet $p$ -Laplacian for triangles and quadrilateral. Pacific J. Math. 288(2017), 425–434.https://doi.org/10.2140/pjm.2017.288.425 CrossRefGoogle Scholar
Pellacci, B. and Verzini, G., Best dispersal strategies in spatially heterogeneous environments: optimization of the principal eigenvalue for indefinite fractional Neumann problems. J. Math. Biol. 76(2018), 1357–1386. https://doi.org/10.1007/s00285-017-1180-z CrossRefGoogle ScholarPubMed
Ryff, J. V., Extreme points of some convex subsets of ${L}^1\left(0,1\right)$ . Proc. Amer. Math. Soc. 18(1967), 1026–1034. https://doi.org/10.1090/s0002-9939-1967-0217586-3 Google Scholar
Servadei, R. and Valdinoci, E., Variational methods for non-local operators of elliptic type. Discrete Contin. Dyn. Syst. 33(2013), 2105–2137. https://doi.org/10.3934/dcds.2013.33.2105 CrossRefGoogle Scholar
Vázquez, J.L., Nonlinear diffusion with fractional Laplacian operators. In: Nonlinear partial differential equations, Abel. Symp. 7(2012), 271–298. https://doi.org/10.1007/978-3-642-25361-4_15 CrossRefGoogle Scholar