Article contents
GCR and CCR Steinberg Algebras
Published online by Cambridge University Press: 23 August 2019
Abstract
Kaplansky introduced the notions of CCR and GCR 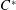 $C^{\ast }$-algebras, because they have a tractable representation theory. Many years later, he introduced the notions of CCR and GCR rings. In this paper we characterize when the algebra of an ample groupoid over a field is CCR and GCR. The results turn out to be exact analogues of the corresponding characterization of locally compact groupoids with CCR and GCR
$C^{\ast }$-algebras, because they have a tractable representation theory. Many years later, he introduced the notions of CCR and GCR rings. In this paper we characterize when the algebra of an ample groupoid over a field is CCR and GCR. The results turn out to be exact analogues of the corresponding characterization of locally compact groupoids with CCR and GCR 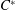 $C^{\ast }$-algebras. As a consequence, we classify the CCR and GCR Leavitt path algebras.
$C^{\ast }$-algebras. As a consequence, we classify the CCR and GCR Leavitt path algebras.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
The second author thanks the Fulbright Commission for sponsoring his stay at the Universidade Federal de Santa Catarina in Florianopolis, Brazil where much of this work was done. The third author was supported in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001.
References
- 3
- Cited by


