Hostname: page-component-5b777bbd6c-j65dx Total loading time: 0 Render date: 2025-06-18T19:31:27.639Z Has data issue: false hasContentIssue false
  • English
  • Français

Matched pairs and Yetter–Drinfeld braces

Part of: Hopf algebras, quantum groups and related topics

Published online by Cambridge University Press:  03 April 2025

Davide Ferri Open the ORCID record for Davide Ferri [Opens in a new window]  and
Andrea Sciandra Open the ORCID record for Andrea Sciandra [Opens in a new window]
Davide Ferri
Affiliation:
Department of Mathematics “G. Peano”, University of Turin, via Carlo Alberto 10, Torino 10123, Italy Department of Mathematics & Data Science, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussels, Belgium e-mail: d.ferri@unito.it Davide.Ferri@vub.be
Andrea Sciandra*
Affiliation:
Department of Mathematics “G. Peano”, University of Turin, via Carlo Alberto 10, Torino 10123, Italy
*
e-mail: andrea.sciandra@unito.it
Get access Rights & Permissions [Opens in a new window]

Abstract

It is proven that a matched pair of actions on a Hopf algebra H is equivalent to the datum of a Yetter–Drinfeld brace, which is a novel structure generalizing Hopf braces. This [-30pt] improves a theorem by Angiono, Galindo, and Vendramin, originally stated for cocommutative Hopf braces. These Yetter–Drinfeld braces produce Hopf algebras in the category of Yetter–Drinfeld modules over H, through an operation that generalizes Majid’s transmutation. A characterization of Yetter–Drinfeld braces via 1-cocycles, in analogy to the one for Hopf braces, is given.

Every coquasitriangular Hopf algebra H will be seen to yield a Yetter–Drinfeld brace, where the additional structure on H is given by the transmutation. We compute explicit examples of Yetter–Drinfeld braces on the Sweedler’s Hopf algebra, on the algebras 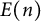$E(n)$, on 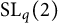$\mathrm {SL}_{q}(2)$, and an example in the class of Suzuki algebras.

Keywords

Yetter–Drinfeld bracesmatched pairsHopf bracesquasitriangular Hopf algebrasbraiding operators

MSC classification

Primary: 16T05: Hopf algebras and their applications
Secondary: 16T25: Yang-Baxter equations
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 37
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The authors were partially supported by the Ministry for University and Research (MUR) within the National Research Project (PRIN 2022) “Structures for Quivers, Algebras and Representations” (SQUARE) Project 2022S97PMY. The first-named author was partially funded by the Vrije Universiteit Brussel Bench Fee for a Joint Doctoral Project, grant number OZR4257, and partially supported through the FWO Senior Research Project G004124N.

References

Agore, A.-L., Classifying bicrossed products of two Taft algebras . J. Pure Appl. Algebra 222(2018), no. 4, 914–930.Google Scholar
Agore, A.-L., Caenepeel, S., and Militaru, G., Braidings on the category of bimodules, Azumaya algebras and epimorphisms of rings . Appl. Categ. Structures 22(2014), no. 1, 29–42.Google Scholar
Andruskiewitsch, N., On the quiver-theoretical quantum Yang–Baxter equation . Selecta Math. 11(2005), no. 2, 203–246.Google Scholar
Andruskiewitsch, N. and Schneider, H.-J., Pointed Hopf algebras . In: New directions in Hopf algebras, volume 43 of Mathematical Sciences Research Institute Publications, Cambridge University Press, Cambridge, 2002, pp. 1–68.Google Scholar
Angiono, I., Galindo, C., and Vendramin, L., Hopf braces and Yang–Baxter operators . Proc. Amer. Math. Soc. 145(2017), no. 5, 1981–1995.Google Scholar
Bontea, C.-G., Classifying bicrossed products of two Sweedler’s Hopf algebras . Czechoslovak Math. J. 64(2014), no. 139(2), 419–431.Google Scholar
Brzeziński, T., Trusses: Between braces and rings . Trans. Amer. Math. Soc. 372(2019), no. 6, 4149–4176.Google Scholar
Caenepeel, S., Militaru, G., and Zhu, S., Frobenius and separable functors for generalized module categories and nonlinear equations, volume 1787 of Lecture Notes in Mathematics, Springer-Verlag, Berlin, 2002.Google Scholar
Carnovale, G. and Cuadra, J., Cocycle twisting of E(n)-module algebras and applications to the Brauer group . K-Theory 33 (2004), no. 3, 251–276.Google Scholar
Doi, Y., Braided bialgebras and quadratic bialgebras . Commun. Algebra 21(1993), no. 5, 1731–1749.Google Scholar
Drinfeld, V. G., Quasi-Hopf algebras and Knizhnik-Zamolodchikov equations . In Problems of modern quantum field theory (Alushta, 1989), Res. Rep. Phys. Springer, Berlin, 1989, pp. 1–13.Google Scholar
Drinfeld, V. G., On some unsolved problems in quantum group theory . In Quantum groups (Leningrad, 1990), vol. 1510 of Lecture Notes in Math., Springer, Berlin, 1992, pp. 1–8.Google Scholar
Etingof, P., Schedler, T., and Soloviev, A., Set-theoretical solutions to the quantum Yang–Baxter equation . Duke Math. J. 100(1999), no. 2, 169.Google Scholar
Faddeev, L. D., Reshetikhin, N. Y., and Takhtajan, L. A., Quantization of Lie groups and Lie algebras . Algebraic Anal. 1(1988), 129–139.Google Scholar
Fernández Vilaboa, J. M., González Rodríguez, R., Ramos Pérez, B., and Rodríguez Raposo, A. B., Modules over invertible 1-cocycles. Turkish J. Math. 48(2024), no. 2, 248–266.Google Scholar
Gateva-Ivanova, T., Set-theoretic solutions of the Yang–Baxter equation, braces and symmetric groups . Adv. Math. 338(2018), 649–701.Google Scholar
Gelaki, S., Topics on quasitriangular Hopf algebras. Master’s Thesis, Ben Gurion University of the Negev, Israel, 1992.Google Scholar
Guarnieri, L. and Vendramin, L., Skew braces and the Yang–Baxter equation . Math. Comput., 86(2017), no. 307, 2519–2534.Google Scholar
Heckenberger, I. and Schneider, H.-J., Hopf algebras and root systems, vol. 247 of Mathematical Surveys and Monographs. American Mathematical Society, Providence, RI, [2020], ©2020.Google Scholar
Joyal, A. and Street, R., Braided tensor categories . Adv. Math. 102(1993), no. 1, 20–78.Google Scholar
Kassel, C., Quantum groups. Vol. 155 of Graduate Texts in Mathematics. Springer-Verlag, New York, 1995.Google Scholar
Kharchenko, V. K., Connected braided Hopf algebras . J. Algebra 307(2007), no. 1, 24–48.Google Scholar
Larson, R. G. and Towber, J., Two dual classes of bialgebras related to the concepts of “quantum group” and “quantum Lie algebra” . Commun. Algebra 19(1991), no. 12, 3295–3345.Google Scholar
Lu, J.-H., Yan, M., and Zhu, Y.-C., On the set-theoretical Yang–Baxter equation . Duke Math. J. 104(2000), no. 1, 1–18.Google Scholar
Majid, S., Physics for algebraists: Non-commutative and non-cocommutative Hopf algebras by a bicrossproduct construction . J. Algebra 130(1990), no. 1, 17–64.Google Scholar
Majid, S., Braided groups and algebraic quantum field theories . Lett. Math. Phys. 22(1991), 167–175.Google Scholar
Majid, S., Braided groups . J. Pure Appl. Algebra 86(1993), no. 2, 187–221.Google Scholar
Majid, S., Transmutation theory and rank for quantum braided groups . Math. Proc. Cambridge Philos. Soc. 113(1993), 45–70.Google Scholar
Majid, S., Algebras and Hopf algebras in braided categories . In Advances in Hopf algebras, (Chicago, IL, 1992), vol. 158 of Lecture Notes in Pure and Appl. Math. Dekker, New York, 1994, pp. 55–105.Google Scholar
Majid, S., Foundations of quantum group theory. Cambridge University Press, Cambridge, 1995.Google Scholar
Martin-Lyons, I. and Truman, P. J., Skew bracoids . J. Algebra, 638(2024), 751–787.Google Scholar
Masuoka, A., Cohomology and coquasi-bialgebra extensions associated to a matched pair of bialgebras . Adv. Math. 173(2003), no. 2, 262–315.Google Scholar
Matsumoto, D. K., Dynamical braces and dynamical Yang–Baxter maps . J. Pure Appl. Algebra 217(2013), no. 2, 195–206.Google Scholar
Panaite, F. and Van Oystaeyen, F., Quasitriangular structures for some pointed Hopf algebras of dimension 2n . Commun. Algebra 27(1999), 4929–4942.Google Scholar
Rump, W., Braces, radical rings, and the quantum Yang–Baxter equation . J. Algebra 307(2007), no. 1, 153–170.Google Scholar
Schauenburg, P., On coquasitriangular Hopf algebras and the quantum Yang-Baxter equation, volume 67 of Algebra Berichte [Algebra Reports], Verlag Reinhard Fischer, Munich, 1992.Google Scholar
Singer, W. M., Extension theory for connected Hopf algebras . J. Algebra 21(1972), no. 1, 1–16.Google Scholar
Suzuki, S., A family of braided cosemisimple Hopf algebras of finite dimension . Tsukuba J. Math. 22(1998), 06.Google Scholar
Takeuchi, M., Survey of braided Hopf algebras . Contemp. Math. 267(2000), no. 8, 301–323.Google Scholar
Tambara, D., The coendomorphism bialgebra of an algebra . J. Faculty Sci. Univ. Tokyo, Section IA, Math. 37(1990), no. 2, 425–456.Google Scholar
Zhu, H., Relative Yetter–Drinfeld modules and comodules over braided groups . J. Math. Phys. 56(2015), no. 4, 41706.Google Scholar