Hostname: page-component-7dd5485656-bt4hw Total loading time: 0 Render date: 2025-10-31T16:48:14.201Z Has data issue: false hasContentIssue false
  • English
  • Français

On the number of linearly independent admissible solutions to linear differential and linear difference equations

Part of: Entire and meromorphic functions, and related topics Differential equations in the complex domain

Published online by Cambridge University Press:  30 July 2020

Janne Heittokangas ,
Hui Yu  and
Mohamed Amine Zemirni
Janne Heittokangas
Affiliation:
Department of Physics and Mathematics, University of Eastern Finland, 80101 Joensuu, P.O. Box 111, Finland e-mail: janne.heittokangas@uef.fi amine.zemirni@uef.fi
Hui Yu*
Affiliation:
Department of Physics and Mathematics, University of Eastern Finland, 80101 Joensuu, P.O. Box 111, Finland e-mail: janne.heittokangas@uef.fi amine.zemirni@uef.fi
Mohamed Amine Zemirni
Affiliation:
Department of Physics and Mathematics, University of Eastern Finland, 80101 Joensuu, P.O. Box 111, Finland e-mail: janne.heittokangas@uef.fi amine.zemirni@uef.fi
*
e-mail: huiy@uef.fi
Get access Rights & Permissions [Opens in a new window]

Abstract

A classical theorem of Frei states that if 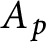$A_p$ is the last transcendental function in the sequence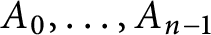$A_0,\ldots ,A_{n-1}$ of entire functions, then each solution base of the differential equation 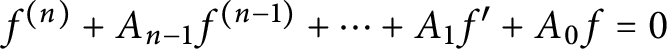$f^{(n)}+A_{n-1}f^{(n-1)}+\cdots +A_{1}f'+A_{0}f=0$ contains at least 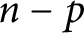$n-p$ entire functions of infinite order. Here, the transcendental coefficient 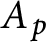$A_p$ dominates the growth of the polynomial coefficients $A_{p+1},\ldots ,A_{n-1}$. By expressing the dominance of 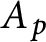$A_p$ in different ways and allowing the coefficients $A_{p+1},\ldots ,A_{n-1}$ to be transcendental, we show that the conclusion of Frei’s theorem still holds along with an additional estimation on the asymptotic lower bound for the growth of solutions. At times, these new refined results give a larger number of linearly independent solutions of infinite order than the original theorem of Frei. For such solutions, we show that 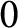$0$ is the only possible finite deficient value. Previously, this property has been known to hold for so-called admissible solutions and is commonly cited as Wittich’s theorem. Analogous results are discussed for linear differential equations in the unit disc, as well as for complex difference and complex q-difference equations.

Keywords

Deficient valuesentire functionsFrei’s theoremlinear difference equationslinear differential equationsWittich’s theorem

MSC classification

Primary: 34M10: Oscillation, growth of solutions
Secondary: 30D35: Distribution of values, Nevanlinna theory

Information

Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 6 , December 2021 , pp. 1556 - 1591
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Barnett, D. C., Halburd, R. G., Morgan, W., and Korhonen, R. J., Nevanlinna theory for the $q$ -difference operator and meromorphic solutions of $q$ -difference equations . Proc. Roy. Soc. Edinburgh Sect. A 137(2007), no. 3, 457–474.CrossRefGoogle Scholar
Bergweiler, W., Ishizaki, K., and Yanagihara, N., Meromorphic solutions of some functional equations . Methods Appl. Anal. 5(1998), no. 3, 248–258.CrossRefGoogle Scholar
Boas, R. P. Jr., Entire functions . Academic Press Inc., New York, 1954.Google Scholar
Chiang, Y. M. and Feng, S. J., On the Nevanlinna characteristic of $f\left(z+\eta \right)$ and difference equations in the complex plane . Ramanujan J. 16(2008), 105–129.CrossRefGoogle Scholar
Chyzhykov, I., Gundersen, G. G., and Heittokangas, J., Linear differential equations and logarithmic derivative estimates . Proc. Lond. Math. Soc. 86(2003), no. 3, 735–754.CrossRefGoogle Scholar
Chyzhykov, I., Gröhn, J., Heittokangas, J., and Rättyä, J., Description of growth and oscillation of solutions of complex LDE’s. Preprint, 2019. https://arxiv.org/pdf/1905.07934v2.pdf Google Scholar
Chyzhykov, I., Heittokangas, J., and Rättyä, J., Finiteness of $\varphi$ -order of solutions of linear differential equations in the unit disc . J. Anal. Math. 109(2009), 163–198.CrossRefGoogle Scholar
Clunie, J., On integral functions having prescribed asymptotic growth . Canad. J. Math. 17(1965), 396–404.CrossRefGoogle Scholar
Frei, M., Über die Lösungen linearer Differentialgleichungen mit ganzen Funktionen als Koeffizienten . Comment. Math. Helv. 35(1961), 201–222 (in German).CrossRefGoogle Scholar
Gundersen, G. G., Estimates for the logarithmic derivative of a meromorphic function, plus similar estimates . J. Lond. Math. Soc. (2) 37(1988), no. 1, 88–104.CrossRefGoogle Scholar
Gundersen, G. G., Heittokangas, J., and Wen, Z. T., Deficient values of solutions of linear differential equations . Comput. Methods Funct. Theory (2020). https://doi.org/10.1007/s40315-020-00320-1CrossRefGoogle Scholar
Gundersen, G. G., Steinbart, E., and Wang, S., The possible orders of solutions of linear differential equations with polynomial coefficients . Trans. Amer. Math. Soc. 350(1998), no. 3, 1225–1247.CrossRefGoogle Scholar
Halburd, R., Korhonen, R., and Tohge, K., Holomorphic curves with shift-invariant hyperplane preimages . Trans. Amer. Math. Soc. 366(2014), no. 8, 4267–4298.CrossRefGoogle Scholar
Hayman, W. K., Meromorphic functions . Oxford Mathematical Monographs, Clarendon Press, Oxford, 1964.Google Scholar
Hayman, W. K., On the characteristic of functions meromorphic in the plane and of their integrals . Proc. Lond. Math. Soc. (3) 14a(1965), 93–128.CrossRefGoogle Scholar
He, Y. Z. and Xiao, X. Z., Algebroid functions and ordinary differential equations . Science Press, Beijing, 1988 (in Chinese).Google Scholar
Heittokangas, J., On complex differential equations in the unit disc . Dissertation, University of Joensuu, Joensuu, 2000. Ann. Acad. Sci. Fenn. Math. Diss. 122(2000), 54.Google Scholar
Heittokangas, J., A survey on Blaschke-oscillatory differential equations, with updates. In: Blaschke products and their applications, Fields Institute Commununications, 65, Springer, New York, 2013, pp. 43–98.CrossRefGoogle Scholar
Heittokangas, J., Korhonen, R., Laine, I., Rieppo, J., and Tohge, K., Complex difference equations of Malmquist type . Comput. Methods Funct. Theory 1(2001), no. 1, 27–39.CrossRefGoogle Scholar
Heittokangas, J., Korhonen, R., and Rättyä, J., Linear differential equations with coefficients in weighted Bergman and Hardy spaces . Trans. Amer. Math. Soc. 360(2008), 1035–1055.CrossRefGoogle Scholar
Heittokangas, J., Korhonen, R., and Rättyä, J., Fast growing solutions of linear differential equations in the unit disc . Results Math. 49(2006), no. 3–4, 265–278.CrossRefGoogle Scholar
Heittokangas, J., Korhonen, R., and Rättyä, J., Growth estimates for solutions of linear complex differential equations . Ann. Acad. Sci. Fenn. Math. 29(2004), no. 1, 233–246.Google Scholar
Heittokangas, J., Latreuch, Z., Wang, J., and Zemirni, M. A., A note on the growth of real functions in sets of positive density. https://arxiv.org/pdf/2006.02066.pdf.Google Scholar
Heittokangas, J. and Wen, Z. T., Functions of finite logarithmic order in the unit disc, Part I . J. Math. Anal. Appl. 415(2014), no. 1, 435–461.CrossRefGoogle Scholar
Korenblum, B., An extension of the Nevanlinna theory . Acta Math. 135(1975), no. 3–4, 187–219.CrossRefGoogle Scholar
Korhonen, R. and Ronkainen, O., Order reduction method for linear difference equations . Proc. Amer. Math. Soc. 139(2011), no. 9, 3219–3229.CrossRefGoogle Scholar
Laine, I., Nevanlinna theory and complex differential equations . De Gruyter Studies in Mathematics, 15, Walter de Gruyter & Co., Berlin, 1993.CrossRefGoogle Scholar
Linden, C. N., Functions analytic in a disc having prescribed asymptotic growth properties . J. Lond. Math. Soc. (2) 2(1970), 267–272.CrossRefGoogle Scholar
Mitrinovic, D. S. and Vasic, M. P., Analytic inequalities . Springer-Verlag, Berlin, 1970.CrossRefGoogle Scholar
Nevanlinna, R., Analytic functions . Springer-Verlag, New York-Berlin, 1970.CrossRefGoogle Scholar
Pachpatte, B. G., Mathematical inequalities. Vol. 67, Elsevier, Amsterdam, 2005.Google Scholar
Tyler, T. F., Maximum curves and isolated points of entire functions . Proc. Amer. Math. Soc. 128(2000), no. 9, 2561–2568.CrossRefGoogle Scholar
Wen, Z. T., Finite logarithmic order solutions of linear $q$ -difference equations . Bull. Korean Math. Soc. 51(2014), no. 1, 83–98.CrossRefGoogle Scholar
Wittich, H., Neuere untersuchungen über eindeutige analytische funktionen . 2nd ed., Springer-Verlag, Berlin-Heidelberg-New York, 1968.CrossRefGoogle Scholar
Yang, C. C. and Yi, H. X., Uniqueness theory of meromorphic functions . Mathematics and its Applications, 557, Kluwer Academic Publishers Group, Dordrecht, 2003.CrossRefGoogle Scholar
Zhang, G. H., Theory of entire and meromorphic functions. Deficient and asymptotic values and singular directions. Translated from the Chinese by Yang, C.-C., Translations of Mathematical Monographs, 122, American Mathematical Society, Providence, RI, 1993.Google Scholar