Article contents
Almost Split Sequences whose Middle Term has at most Two Indecomposable Summands
Published online by Cambridge University Press: 20 November 2018
Extract
Let Λ be an artin algebra, and denote by mod Λ the category of finitely generated Λ-modules. All modules we consider are finitely generated.
We recall from [6] that a nonsplit exact sequence 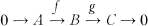 in mod A is said to be almost split if A and C are indecomposable, and given a map h: X → C which is not an isomorphism and with X indecomposable, there is some t: X → B such that gt = h.
in mod A is said to be almost split if A and C are indecomposable, and given a map h: X → C which is not an isomorphism and with X indecomposable, there is some t: X → B such that gt = h.
Almost split sequences have turned out to be useful in the study of representation theory of artin algebras. Given a nonprojective indecomposable Λ-module C (or an indecomposable noninjective Λ-module A), we know that
there exists a unique almost split sequence 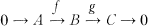 [6, Proposition 4.3], [5, Section 3].
[6, Proposition 4.3], [5, Section 3].
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1979
References
- 12
- Cited by

