Hostname: page-component-784d4fb959-wvrvt Total loading time: 0 Render date: 2025-07-15T05:36:31.323Z Has data issue: false hasContentIssue false
  • English
  • Français

Central Limit Theorem for tensor products of free variables

Part of: Probability theory on algebraic and topological structures Selfadjoint operator algebras Limit theorems General theory of linear operators

Published online by Cambridge University Press:  16 December 2024

Cécilia Lancien ,
Patrick Oliveira Santos  and
Pierre Youssef Open the ORCID record for Pierre Youssef [Opens in a new window]
Cécilia Lancien
Affiliation:
CNRS & Institut Fourier UMR 5582, Université Grenoble Alpes, Grenoble, France e-mail: cecilia.lancien@univ-grenoble-alpes.fr
Patrick Oliveira Santos*
Affiliation:
Laboratoire d’Analyse et de Mathématiques Appliquées UMR 8050, Université Gustave Eiffel, Université Paris Est Créteil, Marne-la-Vallée, France
Pierre Youssef
Affiliation:
Division of Science, NYU Abu Dhabi, Abu Dhabi, UAE and Courant Institute of Mathematical Sciences, New York University, New York, United States e-mail: yp27@nyu.edu
*
e-mail: patrick.oliveirasantos@u-pem.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

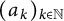We establish a Central Limit Theorem for tensor product random variables $c_k:=a_k \otimes a_k$, where $(a_k)_{k \in \mathbb {N}}$ is a free family of variables. We show that if the variables 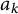$a_k$ are centered, the limiting law is the semi-circle. Otherwise, the limiting law depends on the mean and variance of the variables 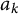$a_k$ and corresponds to a free interpolation between the semi-circle law and the classical convolution of two semi-circle laws.

Keywords

Central Limit Theoremtensor productsfree random variablesnoncommutative probability space

MSC classification

Primary: 46L54: Free probability and free operator algebras 47A80: Tensor products of operators 60B20: Random matrices (probabilistic aspects; for algebraic aspects see ) 60F05: Central limit and other weak theorems

Information

Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 33
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Part of this work was initiated during a stay of the second named author at New York University in Abu Dhabi, partly funded by a doctoral mobility grant delivered by Université Gustave Eiffel; he would like to thank both institutions for their support and the excellent working assumptions. The first named author was supported by the ANR projects ESQuisses (Grant No. ANR-20-CE47-0014-01), STARS (Grant No. ANR-20-CE40-0008), and QTraj (Grant No. ANR-20-CE40-0024-01).

References

Ambainis, A., Harrow, A. W., and Hastings, M. B., Random tensor theory: Extending random matrix theory to mixtures of random product states . Commun. Math. Phys. 310(2012), no. 1, 25–74. https://doi.org/10.1007/s00220-011-1411-x Google Scholar
Aubrun, G. and Nechita, I., Realigning random states . J. Math. Phys. 53(2012), no 10, 102210.Google Scholar
Bożejko, M. and Speicher, R., Interpolations between bosonic and fermionic relations given by generalized brownian motions . Mathematische Zeitschrift 222(1996), no. 1, 135–160. https://doi.org/10.1007/BF02621861 Google Scholar
Bożejko, M. and Speicher, R., Interpolations between bosonic and fermionic relations given by generalized Brownian motions . Math. Z. 222(1996), no. 1, 135–159. https://doi.org/10.1007/PL00004258 Google Scholar
Collins, B. and Lamarre, P. Y. G., $\ast$ -Freeness in finite tensor products . Adv. Appl. Math. 83(2017), 47–80.Google Scholar
Dehornoy, P. and Biane, P., Dual garside structure of braids and free cumulants of products . Séminaire Lotharingien de Combinatoire 72(2014), 15.Google Scholar
Gouyou-Beauchamps, D., Chemins sous-diagonaux et tableaux de Young, Springer, Berlin Heidelberg, 1986, pp. 112–125. https://doi.org/10.1007/BFb0072513 Google Scholar
Lancien, C., Santos, P. O., and Youssef, P., Limiting spectral distribution of random self-adjoint quantum channels . Math Phys Anal Geom 27(2024), no. 15. https://doi.org/10.1007/s11040-024-09482-z Google Scholar
Lehner, F., Free cumulants and enumeration of connected partitions . Eur. J. Combin. 23(2002), no. 8, 1025–1031. https://doi.org/10.1006/eujc.2002.0619 Google Scholar
Młotkowski, W., A-free probability . Infin. Dimens. Anal., Quant. Probab. Relat. Topics 07(2004), no. 01, 27–41. https://doi.org/10.1142/S0219025704001517 Google Scholar
Nica, A., Free probability aspect of irreducible meandric systems, and some related observations about meanders . Infin. Dimens. Anal., Quant. Probab. Relat. Topics 19(2016), no. 02, 1650011. https://doi.org/10.1142/s0219025716500119 Google Scholar
Nica, A. and Speicher, R.. Lectures on the combinatorics of free probability. Vol. 13, Cambridge University Press, 2006.Google Scholar
Nijenhuis, A. and Wilf, H. S., The enumeration of connected graphs and linked diagrams . J. Combin. Theory Ser. A 27(1979), no. 3, 356–359. https://doi.org/10.1016/0097-3165(79)90023-2.Google Scholar
Speicher, R. and Weber, M., Quantum groups with partial commutation relations . Indiana Univ. Math. J. 68(2019), no. 6, 1849–1883.Google Scholar
Speicher, R. and Wysoczański, J., Mixtures of classical and free independence . Archiv der Mathematik 107(Sep. 2016), no. 4, 445–453. https://doi.org/10.1007/s00013-016-0955-6 Google Scholar
Voiculescu, D., Symmetries of some reduced free product C*-algebras, Springer, Berlin, 1985, pp. 556–588. https://doi.org/10.1007/BFb0074909 Google Scholar