Hostname: page-component-7dd5485656-tbj44 Total loading time: 0 Render date: 2025-10-31T16:06:23.823Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterizations of Continuous and Discrete q-Ultraspherical Polynomials

Published online by Cambridge University Press:  20 November 2018

Mourad E. H. Ismail  and
Josef Obermaier
Mourad E. H. Ismail
Affiliation:
Department of Mathematics, City University of Hong Kong, Tat Chee Avenue, Kowloon, Hong Kong and Department of Mathematics, King Saud University, Riyadh, Saudi Arabia email: ismail@math.ucf.edu
Josef Obermaier
Affiliation:
Helmholtz Zentrum München, German Research Center for Environmental Health, Institute of Biomathematics and Biometry, Ingolstädter Landstr. 1, 85764 Neuherberg, Germany email: josef.obermaier@helmholtz-muenchen.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We characterize the continuous q-ultraspherical polynomials in terms of the special form of the coefficients in the expansion 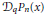${{\mathcal{D}}_{q}}{{P}_{n}}\left( x \right)$ in the basis 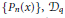$\left\{ {{P}_{n}}\left( x \right) \right\},{{\mathcal{D}}_{q}}$ being the Askey-Wilson divided difference operator. The polynomials are assumed to be symmetric, and the connection coefficients are multiples of the reciprocal of the square of the 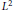${{L}^{2}}$ norm of the polynomials. A similar characterization is given for the discrete $q$ -ultraspherical polynomials. A new proof of the evaluation of the connection coefficients for big $q$ -Jacobi polynomials is given.

Keywords

33D4542C05continuous q-ultraspherical polynomialsbig q-Jacobi polynomialsdiscrete q-ultraspherical polynomialsAskey–Wilson operatorq-difference operatorrecursion coefficients

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 1 , 01 February 2011 , pp. 181 - 199
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Al-Salam, W.A., Characterization theorems for orthogonal polynomials. In: Orthogonal Polynomials (Columbus, OH, 1989), NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci., 294, Kluwer Acad. Publ., Dordrecht, 1990, pp. 1-24.Google Scholar
[2] Al-Salam, W.A. and Chihara, T. S., Convolutions of orthogonal polynomials. SIAM J. Math. Anal. 7 (1976), no. 1, 16-28. doi:10.1137/0507003Google Scholar
[3] Al-Salam, W.A. and Chihara, T. S., q-Pollaczek polynomials and a conjecture of Andrews and Askey. SIAM J. Math. Anal. 18 (1987), no. 1, 228-242. doi:10.1137/0518018Google Scholar
[4] Andrews, G. E., On q-analogues of the Watson and Whipple summations. SIAM J. Math. Anal. 7 (1976), no. 3, 332-336. doi:10.1137/0507026Google Scholar
[5] Andrews, G. E. and Askey, R., Enumeration of partitions: the role of Eulerian series and q-orthogonal polynomials. In: Higher combinatorics (Proc. NATO Advanced Study Inst., Berlin, 1976), NATO Adv. Study Inst. Ser., Ser. C: Math. Phys. Sci., 31, Reidel, Dordrecht-Boston, Mass., 1977, pp. 3-26.Google Scholar
[6] Andrews, G. E. and Askey, R., Classical orthogonal polynomials. In: Orthogonal polynomials and applications, Lecture Notes in Math., 1171, Springer, Berlin, 1985, pp. 36-63.Google Scholar
[7] Andrews, G. E., Askey, R., and Roy, R., Special functions. Encyclopedia of Mathematics and its Applications, 71, Cambridge University Press, Cambridge, 1999.Google Scholar
[8] Askey, R. A. and Ismail, M. E. H., A generalization of the ultraspherical polynomials. In: Studies in pure mathematics, Birkhäuser, Basel, 1983, pp. 55-78.Google Scholar
[9] Askey, R. A. and M. Ismail, E. H., Recurrence relations, continued fractions, and orthogonal polynomials. Mem. Amer. Math. Soc. 49 (1984), no. 300, 108 pp.Google Scholar
[10] Askey, R. and, J. Wilson, Some basic hypergeometric orthogonal polynomials that generalize Jacobi polynomials. Mem. Amer. Math. Soc. 54 (1985), no. 319, 55 pp.Google Scholar
[11] Feldheim, E., Sur les polynômes gènèralisès de Legendre. Bull. Acad. Sci. URSS. Sèr. Math. [Izvestia Akad. Nauk SSSR] 5 (1941), 241-254.Google Scholar
[12] Gasper, G. and, Rahman, M., Basic hypergeometric series. Second ed., Encyclopedia of Mathematics and its Applications, 96, Cambridge University Press, Cambridge, 2004.Google Scholar
[13] Ismail, M. E. H., Classical and quantum orthogonal polynomials in one variable. Encyclopedia of Mathematics and its Applications, 98, Cambridge University Press, Cambridge, 2005.Google Scholar
[14] Koekoek, R. and, Swarttouw, R. F., The Askey-scheme of hypergeometric orthogonal polynomials and its q-analogue. Reports of the Faculty of Technical Mathematics and Informatics, 98-17, Delft University of Technology, Delft, 1998.Google Scholar
[15] Lanzewizky, I. L., Über die Orthogonalität der Fèjèr-Szegöschen Polynome. C. R. (Doklady) Acad. Sci. URSS (N. S.) 31 (1941), 199-200.Google Scholar
[16] Lasser, R. and, Obermaier, J., A new characterization of ultraspherical polynomials. Proc. Amer. Math. Soc. 136 (2008), no. 7, 2493-2498. doi:10.1090/S0002-9939-08-09378-7Google Scholar
[17] Müller, C., Analysis of spherical symmetries in Euclidean spaces. Applied Mathematical Sciences, 129, Springer-Verlag, Berlin, 1998.Google Scholar
[18] Szegő, G., Orthogonal polynomials. Fourth ed., Colloquium Publications, XXIII, American Mathematical Society, Providence, RI, 1975.Google Scholar