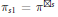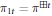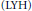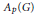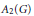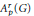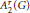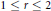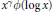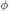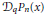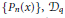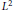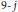Contents
Award Winners
Research Article
Free Bessel Laws
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-37
-
- Article
-
- You have access
- Export citation
Research Article
Asymptotic Formulae for Pairs of Diagonal Cubic Equations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 38-54
-
- Article
-
- You have access
- Export citation
Pseudolocality for the Ricci Flow and Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 55-85
-
- Article
-
- You have access
- Export citation
On Vojta's 1 + Ɛ Conjecture
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 86-103
-
- Article
-
- You have access
- Export citation
Reversibility of Interacting Fleming–Viot Processes with Mutation, Selection, and Recombination
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 104-122
-
- Article
-
- You have access
- Export citation
Strong and Extremely Strong Ditkin sets forthe Banach Algebras Apr (G) = A p ⋂ L r (G)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 123-135
-
- Article
-
- You have access
- Export citation
Transcendental Nature of Special Values of L-Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 136-152
-
- Article
-
- You have access
- Export citation
Asymptotics for Functions Associated with Heat Flow on the Sierpinski Carpet
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 153-180
-
- Article
-
- You have access
- Export citation
Characterizations of Continuous and Discrete q-Ultraspherical Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 181-199
-
- Article
-
- You have access
- Export citation
An Explicit Polynomial Expression for a q-Analogue of the 9- j Symbols
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 200-221
-
- Article
-
- You have access
- Export citation
Limit Theorems for Additive Conditionally Free Convolution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 222-240
-
- Article
-
- You have access
- Export citation