Article contents
Fourier coefficients of minimal and next-to-minimal automorphic representations of simply-laced groups
Published online by Cambridge University Press: 21 September 2020
Abstract
In this paper, we analyze Fourier coefficients of automorphic forms on a finite cover G of an adelic split simply-laced group. Let 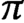 $\pi $ be a minimal or next-to-minimal automorphic representation of G. We prove that any
$\pi $ be a minimal or next-to-minimal automorphic representation of G. We prove that any 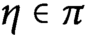 $\eta \in \pi $ is completely determined by its Whittaker coefficients with respect to (possibly degenerate) characters of the unipotent radical of a fixed Borel subgroup, analogously to the Piatetski-Shapiro–Shalika formula for cusp forms on
$\eta \in \pi $ is completely determined by its Whittaker coefficients with respect to (possibly degenerate) characters of the unipotent radical of a fixed Borel subgroup, analogously to the Piatetski-Shapiro–Shalika formula for cusp forms on 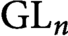 $\operatorname {GL}_n$. We also derive explicit formulas expressing the form, as well as all its maximal parabolic Fourier coefficient, in terms of these Whittaker coefficients. A consequence of our results is the nonexistence of cusp forms in the minimal and next-to-minimal automorphic spectrum. We provide detailed examples for G of type
$\operatorname {GL}_n$. We also derive explicit formulas expressing the form, as well as all its maximal parabolic Fourier coefficient, in terms of these Whittaker coefficients. A consequence of our results is the nonexistence of cusp forms in the minimal and next-to-minimal automorphic spectrum. We provide detailed examples for G of type 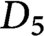 $D_5$ and
$D_5$ and 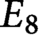 $E_8$ with a view toward applications to scattering amplitudes in string theory.
$E_8$ with a view toward applications to scattering amplitudes in string theory.
Keywords
MSC classification
Information
- Type
- Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © Canadian Mathematical Society 2020
References
- 5
- Cited by


