Suppose that 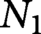$N_1$ and 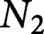$N_2$ are closed smooth manifolds of dimension n that are homeomorphic. We prove that the spaces of smooth knots, 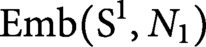$ \operatorname {\mathrm {Emb}}(\mathrm {S}^1, N_1)$ and 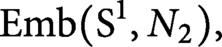$ \operatorname {\mathrm {Emb}}(\mathrm {S}^1, N_2),$ have the same homotopy 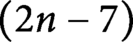$(2n-7)$-type. In the four-dimensional case, this means that the spaces of smooth knots in homeomorphic 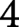$4$-manifolds have sets 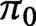$\pi _0$ of components that are in bijection, and the corresponding path components have the same fundamental groups 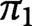$\pi _1$. The result about 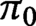$\pi _0$ is well-known and elementary, but the result about 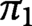$\pi _1$ appears to be new. The result gives a negative partial answer to a question of Oleg Viro. Our proof uses the Goodwillie–Weiss embedding tower. We give a new model for the quadratic stage of the Goodwillie–Weiss tower, and prove that the homotopy type of the quadratic approximation of the space of knots in N does not depend on the smooth structure on N. Our results also give a lower bound on 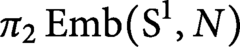$\pi _2 \operatorname {\mathrm {Emb}}(\mathrm {S}^1, N)$. We use our model to show that for every choice of basepoint, each of the homotopy groups, 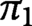$\pi _1$ and 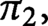$\pi _2,$ of 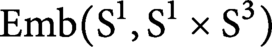$ \operatorname {\mathrm {Emb}}(\mathrm {S}^1, \mathrm {S}^1\times \mathrm {S}^3)$ contains an infinitely generated free abelian group.

The asymptotic behavior of solutions to a family of Dirichlet boundary value problems, involving differential operators in divergence form, on a domain equipped with a Finsler metric is investigated. Solutions are shown to converge uniformly to the distance function to the boundary of the domain, which takes into account the Finsler norm involved in the equation. This implies that a well-known result in the analysis of problems modeling torsional creep continues to hold in this more general setting.

We classify real two-dimensional orbits of conformal subgroups such that the orbits contain two circular arcs through a point. Such surfaces must be toric and admit a Möbius automorphism group of dimension at least two. Our theorem generalizes the classical classification of Dupin cyclides.

We present a new approach to graph limit theory that unifies and generalizes the two most well-developed directions, namely dense graph limits (even the more general $L^p$ limits) and Benjamini–Schramm limits (even in the stronger local-global setting). We illustrate by examples that this new framework provides a rich limit theory with natural limit objects for graphs of intermediate density. Moreover, it provides a limit theory for bounded operators (called P-operators) of the form $L^\infty (\Omega )\to L^1(\Omega )$ for probability spaces $\Omega $. We introduce a metric to compare P-operators (for example, finite matrices) even if they act on different spaces. We prove a compactness result, which implies that, in appropriate norms, limits of uniformly bounded P-operators can again be represented by P-operators. We show that limits of operators, representing graphs, are self-adjoint, positivity-preserving P-operators called graphops. Graphons, $L^p$ graphons, and graphings (known from graph limit theory) are special examples of graphops. We describe a new point of view on random matrix theory using our operator limit framework.

In this paper, we analyze Fourier coefficients of automorphic forms on a finite cover G of an adelic split simply-laced group. Let $\pi $ be a minimal or next-to-minimal automorphic representation of G. We prove that any $\eta \in \pi $ is completely determined by its Whittaker coefficients with respect to (possibly degenerate) characters of the unipotent radical of a fixed Borel subgroup, analogously to the Piatetski-Shapiro–Shalika formula for cusp forms on $\operatorname {GL}_n$. We also derive explicit formulas expressing the form, as well as all its maximal parabolic Fourier coefficient, in terms of these Whittaker coefficients. A consequence of our results is the nonexistence of cusp forms in the minimal and next-to-minimal automorphic spectrum. We provide detailed examples for G of type $D_5$ and $E_8$ with a view toward applications to scattering amplitudes in string theory.

Let $\mathcal {N}(b)$ be the set of real numbers that are normal to base b. A well-known result of Ki and Linton [19] is that $\mathcal {N}(b)$ is $\boldsymbol {\Pi }^0_3$-complete. We show that the set ${\mathcal {N}}^\perp (b)$ of reals, which preserve $\mathcal {N}(b)$ under addition, is also $\boldsymbol {\Pi }^0_3$-complete. We use the characterization of ${\mathcal {N}}^\perp (b),$ given by Rauzy, in terms of an entropy-like quantity called the noise. It follows from our results that no further characterization theorems could result in a still better bound on the complexity of ${\mathcal {N}}^\perp (b)$. We compute the exact descriptive complexity of other naturally occurring sets associated with noise. One of these is complete at the $\boldsymbol {\Pi }^0_4$ level. Finally, we get upper and lower bounds on the Hausdorff dimension of the level sets associated with the noise.

We construct a family of compactifications of the affine cone of the Grassmannian variety of $2$-planes. We show that both the tropical variety of the Plücker ideal and familiar valuations associated to the construction of Newton–Okounkov bodies for the Grassmannian variety can be recovered from these compactifications. In this way, we unite various perspectives for constructing toric degenerations of flag varieties.

Let $a_1$, $a_2$, and $a_3$ be distinct reduced residues modulo q satisfying the congruences $a_1^2 \equiv a_2^2 \equiv a_3^2 \ (\mathrm{mod}\ q)$. We conditionally derive an asymptotic formula, with an error term that has a power savings in q, for the logarithmic density of the set of real numbers x for which $\pi (x;q,a_1)> \pi (x;q,a_2) > \pi (x;q,a_3)$. The relationship among the $a_i$ allows us to normalize the error terms for the $\pi (x;q,a_i)$ in an atypical way that creates mutual independence among their distributions, and also allows for a proof technique that uses only elementary tools from probability.

Let A be a two-dimensional abelian variety defined over a number field K. Fix a prime number $\ell $ and suppose $\#A({\mathbf {F}_{\mathfrak {p}}}) \equiv 0 \pmod {\ell ^2}$ for a set of primes ${\mathfrak {p}} \subset {\mathcal {O}_{K}}$ of density 1. When $\ell =2$ Serre has shown that there does not necessarily exist a K-isogenous $A'$ such that $\#A'(K)_{{tor}} \equiv 0 \pmod {4}$. We extend those results to all odd $\ell $ and classify the abelian varieties that fail this divisibility principle for torsion in terms of the image of the mod-$\ell ^2$ representation.