Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chandra, Prem
and
Mohapatra, R. N.
1983.
General Inequalities 3.
Vol. 64,
Issue. ,
p.
455.
Mitrinović, D. S.
Pečarić, J. E.
and
Fink, A. M.
1991.
Inequalities Involving Functions and Their Integrals and Derivatives.
p.
143.
Kumar, Manish
and
Mohapatra, R. N.
2019.
Differential and Integral Inequalities.
Vol. 151,
Issue. ,
p.
549.

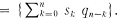 . The
. The 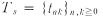 defined by t
defined by t