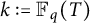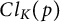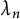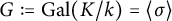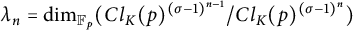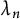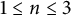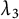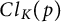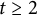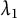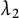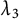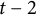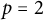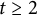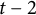1 Introduction
There have been active studies on the structure of the class groups of number fields and function fields; for instance, we refer to [Reference Anglés and Jaulent1–Reference Conner and Hurrelbrink5, Reference Gauss6, Reference Hu and Li8, Reference Ichimura10, Reference Lee and Yoo11, Reference Rédei and Reichardt13–Reference Rosen16, Reference Wittmann19–Reference Zhao and Hu25]. For studying the structure of class groups, the following methods have been used: genus theory [Reference Anglés and Jaulent1, Reference Bae and Koo3, Reference Gauss6], Rédei matrix [Reference Bae, Hu and Jung2, Reference Rédei and Reichardt15, Reference Yue23], and Conner and Hurrelbrink’s exact hexagon [Reference Conner and Hurrelbrink5, Reference Peng13].
The Galois module structure of the class groups of cyclic extensions over the rational function field
$k:={\mathbb F}_q(T)$
has been studied in [Reference Bae, Hu and Jung2, Reference Hu and Li8, Reference Peng14, Reference Wittmann19], where
${\mathbb F}_q$
is a finite field of order q. We need to introduce the following definitions for description of the previous developments. Let K be a cyclic extension over k of extension degree prime p. We denote the ideal class group of K by
$Cl_K$
and that of divisor class group by
$J_K$
. Let
$G := \mathrm{Gal}(K/k)$
be the Galois group of K over k. Then
$Cl_K$
and
$J_K$
are finite G-modules. Let
${\sigma }$
be a generator of G and
${\mathbb Z}_p$
the ring of p-adic integer. The structures of
$Cl_K(p)$
and
$J_K(p)$
as finite modules over the discrete valuation ring
${\mathbb Z}_p[{\sigma }]/(1 + {\sigma } + \cdots + {\sigma }^{p-1}) \simeq {\mathbb Z}_p[\zeta _p]$
are determined by the following ranks:
$$ \begin{align*} {\lambda}_n &:= \dim_{{\mathbb F}_p}(Cl_K(p)^{({\sigma}-1)^{n-1}}/Cl_K(p)^{({\sigma}-1)^n}) \quad \mbox{and}\\ {\mu}_n &:= \dim_{{\mathbb F}_p}(J_K(p)^{({\sigma}-1)^{n-1}}/J_K(p)^{({\sigma}-1)^n}), \end{align*} $$
where
$Cl_K(p)$
(resp.
$J_K(p)$
) is the p-Sylow subgroup of
$Cl_K$
(resp.
$J_K$
) and
$\zeta _p$
is a primitive pth root of unity.
We point out that in particular, when
$p = 2$
, the rank
${\lambda }_n$
of
$Cl_K$
is exactly equal to the
$2^n$
-rank of
$Cl_K$
and the rank
${\mu }_n$
of
$J_K$
gives the
$2^n$
-rank of
$J_K$
, where the
$2^n$
-rank of
$Cl_K$
is defined as
$\dim _{{\mathbb F}_2}(Cl_K^{2^{n-1}} /Cl_K^{2^n})$
and similarly for
$J_K$
. This is because
${\sigma }$
acts
$-1$
on
$Cl_K$
, which implies that the rank
${\lambda }_n$
of the finite module
$Cl_K$
over
${\mathbb Z}[\zeta _2] = {\mathbb Z}$
is exactly the
$2^n$
-rank of
$Cl_K$
, and similarly it also holds for
$J_K$
.
There are exactly two kinds of cyclic extensions of prime extension degree over the rational function field k: Kummer extension and Artin–Schreier extension. For Kummer extensions L over k, Anglés and Jaulent [Reference Anglés and Jaulent1] (resp. Wittmann [Reference Wittmann19]) studied the
${\lambda }_1$
-rank (resp.
${\lambda }_2$
-rank) of the ideal class groups of L and the authors of this paper [Reference Yoo and Lee22] studied the
${\lambda }_3$
-rank of the ideal class groups of L. Furthermore, for Artin–Schreier extensions over k, there also have been some studies on the computation of
${\lambda }_1$
and
${\lambda }_2$
for their ideal class groups [Reference Bae, Hu and Jung2, Reference Hu and Li8]. However, there has been no result yet on finding infinite families of Artin–Schreier extensions over k whose ideal class groups have guaranteed prescribed
${\lambda }_n$
-rank of the ideal class group of Artin–Schreier extension for
$1 \leq n \leq 3$
. This is one of the motivations of our paper.
In this paper, we study the Galois module structure of the class groups of the Artin–Schreier extensions K over k of extension degree p, where
$k:={\mathbb F}_q(T)$
is the rational function field of characteristic p and p is a prime number. The structure of the p-part
$Cl_K(p)$
of the ideal class group of K as a finite G-module is determined by the invariant
${\lambda }_n$
, where
$G:=\operatorname {\mathrm {Gal}}(K/k)=\langle {\sigma } \rangle $
. In detail, first of all, for a given positive integer t, we obtain infinite families of K over k whose
${\lambda }_1$
-rank of
$Cl_K$
is t and
${\lambda }_n$
-rank of
$Cl_K$
is zero for
$n \ge 2$
, depending on the ramification behavior of the infinite place
$\infty $
of k (Theorems 3.2–3.4). We then find infinite families of the Artin–Schreier extensions over k whose ideal class groups have guaranteed prescribed
${\lambda }_n$
-rank for n up to 3. We find an algorithm for computing
${\lambda }_3$
-rank of
$Cl_K(p)$
. Using this algorithm, for a given integer
$t \ge 2$
, we get infinite families of the Artin–Schreier extensions over k whose
${\lambda }_1$
-rank is t,
${\lambda }_2$
-rank is
$t-1$
, and
${\lambda }_3$
-rank is
$t-2$
(Theorem 5.1). In particular, in the case where
$p=2$
, for a given positive integer
$t \ge 2$
, we obtain an infinite family of the Artin–Schreier quadratic extensions over k which have 2-class group rank exactly t,
$2^2$
-class group rank
$t-1$
, and
$2^3$
-class group rank
$t-2$
(Corollary 5.3). Furthermore, we also obtain a similar result on the
$2^n$
-ranks of the divisor class groups of the Artin–Schreier quadratic extensions over k for n up to 3 (Corollary 5.4). Finally, in Tables 1 and 2, we give some implementation results for explicit infinite families using Theorems 3.2–3.4 and 5.1. These implementation results are done by MAGMA.
We remark that as a main tool for computation of
${\lambda }_3$
, we use an analogue of Rédei matrix. We emphasize that there is no number field analogue for the Artin–Schreier extensions over k, while there is a number field analogue for Kummer extensions over k.
2 Preliminaries
Let q be a power of a prime number p, and let
$k := {\mathbb F}_q(T)$
be the rational function field. The prime divisor of k corresponding to
$(1/T)$
is called the infinite place and denoted by
$\infty $
. Let
$K/k$
be a cyclic extension of degree p. Then
$K/k$
is an Artin–Schreier extension: that is,
$K = k({\alpha })$
, where
${\alpha }^p-{\alpha } = D$
,
$D \in k$
, and that D cannot be written as
$x^p-x$
for any
$x \in k$
. Conversely, for any
$D \in k$
and D cannot be written as
$x^p-x$
for any
$x \in k$
,
$k({\alpha })/k$
is a cyclic extension of degree p, where
${\alpha }^p-{\alpha }=D$
.
For
$D, D' \in k$
, let
$K_1:=k({\alpha })$
and
$K_2:=k({\beta })$
be two Artin–Schreier extensions over k with
${\alpha }^p - {\alpha } = D$
and
${\beta }^p-{\beta } = D'$
, respectively. Two Artin–Schreier extensions
$K_1$
and
$K_2$
are equal if and only if they satisfy the following relations [Reference Hu and Li8, p. 256]:
$$ \begin{align*} &{\alpha} \quad \rightarrow \quad x{\alpha} + B_0 = {\beta},\\[2pt] &D \quad \rightarrow \quad xD+(B_0^p-B_0) = D',\\[2pt] &x \in {\mathbb F}_p^\times, ~B_0 \in k. \end{align*} $$
Thus, D can be normalized to satisfy the following conditions:
$$ \begin{align} &D = \sum_{i=1}^{m} \frac{Q_i}{P_i^{r_i}} + f(T),\\ &(P_i, Q_i) = 1, ~p \nmid r_i \mbox{ for } 1 \leq i \leq t,\nonumber \\ &p \nmid \deg f(T) \; \mbox{ if } \deg {f(T)} \geq 1, \mbox{ and} \nonumber\\ & {f(T)} =0 \; \mbox{ if } f(T) \in {\mathbb F}_q \mbox{ with } \operatorname{\mathrm{Tr}}_{{\mathbb F}_q/{\mathbb F}_p} (f) = 0, \nonumber \end{align} $$
where
$P_i$
is a monic irreducible polynomial in
${\mathbb F}_q[T]$
,
$Q_i$
,
$f(T) \in {\mathbb F}_q[T]$
, and
$\deg {Q_i} < \deg {P_i^{r_i}}$
for
$1 \leq i \leq t$
; the last condition follows from noting that if
$f(T)=c$
in
${\mathbb F}_q^\times $
with
$\operatorname {\mathrm {Tr}}_{{\mathbb F}_q/{\mathbb F}_p}(c) = 0$
, then there exists
$b \in {\mathbb F}_q^\times $
such that
$b^p-b = c$
.
Throughout this paper, let
be the Artin–Schreier extension over k of extension degree p, where
$x^p-x = D_m$
has no root in k,
is a root of
$x^p-x=D_m$
, and the normalized
$D_m$
satisfies (2.1). We note that all the finite places of k which are totally ramified in K are
$P_1, \dots , P_t$
. In the following lemma, we state the ramification behavior of the infinite place
$\infty $
of k in K.
Lemma 2.1 [Reference Hu and Li8, p. 256]
Let
be the Artin–Schreier extension over k of extension degree p, where
and
$D_m$
is defined in (2.1). Then we have the followings.
-
(i) The infinite place
$\infty $
of k is totally ramified in K if and only if
$\deg {f(T)} \geq 1$
. -
(ii) The infinite place
$\infty $
of k is inert in K if and only if
$f(T) = c \in {\mathbb F}_q^\times $
, where
$x^p-x-c$
is irreducible over
${\mathbb F}_q$
. -
(iii) The infinite place
$\infty $
of k splits completely in K if and only if
$f(T) = 0$
.
For descriptions of
${\lambda }_1$
and
${\lambda }_2$
, we use the notion of the Hasse symbol which is first introduced in [Reference Hasse7].
Definition 2.1 [Reference Hu and Li8, p. 257]
Let
be the Artin–Schreier extension over k of extension degree p, where
for some
$D_m \in k$
. Let P be a finite place of k which is unramified in K, and let
$\left (\frac {K/k}{P}\right )$
be the Artin symbol of P. Then
, where
$\left \{\frac {D_m}{P}\right \}$
is defined as follows:
$$ \begin{align*}\left \{\frac{D_m}{P}\right \} = \operatorname{\mathrm{Tr}}_{(\mathcal{O}_K/P)/{\mathbb F}_p}(D_m \mbox{ mod } P);\end{align*} $$
$\operatorname {\mathrm {Tr}}_{(\mathcal {O}_K/P)/{\mathbb F}_p}$
denotes the trace function from
$\mathcal {O}_K/P$
to
${\mathbb F}_p$
and
$\mathcal {O}_K$
is the integral closure of K. We call
$\left \{\frac {\cdot }{\cdot }\right \}$
the Hasse symbol.
Lemma 2.2 [Reference Hu and Li8]
Let
be the Artin–Schreier extension over k of extension degree p, where
, which is defined in (2.1). Then we have the followings.
-
(i)
${\lambda }_1 = \left \{ \begin {array}{ll} m & \mbox {if}\ \deg f(T) \ge 1\ \mbox { or}\\&\ \ \ \ f(T) = c \in {\mathbb F}_q^\times, \mbox { where}\ x^p-x=c \in {\mathbb F}_q^\times \ \mbox {is irreducible over}\ {\mathbb F}_q,\\[3pt] m-1 & \mbox {if}\ f(T) = 0. \\ \end {array} \right.$
-
(ii) We have
${\lambda }_2 = {\lambda }_1 - \operatorname {\mathrm {rank}}(R)$
, where
$R = [r_{ij}]$
is a matrix over
${\mathbb F}_p$
defined by
$$ \begin{align*}r_{ij} = \left\{ \begin{array}{ll} \left\{\frac{Q_j/P_j^{r_j}}{P_i} \right\}, & \mbox{for } 1 \leq i \neq j \leq m,\\[4pt] -\left(\sum_{j=1, i \neq j}^{m} r_{ij} + \left\{\frac{f}{P_i}\right\} \right), & \mbox{for } 1 \leq i=j \leq m. \end{array} \right.\end{align*} $$
-
We call such matrix R as the Rédei matrix.
We recall that the Hilbert class field
$H_K$
of K is the maximal unramified abelian extension of K where the infinite places of k split completely in K. The genus field
$\mathcal {G}_K$
of K is the maximal subextension
$K \subseteq \mathcal {G}_K \subseteq H_K$
which is abelian over k. In Lemma 2.3, we state a description of the genus field of the Artin–Schreier extension.
Lemma 2.3 [Reference Hu and Li8, Theorem 4.1]
Let
be the Artin–Schreier extension over k of extension degree p, where
$D_m$
is defined in (2.1) and
is a root of
$x^p-x=D_m$
. Let
${\alpha }_i\ ($
resp.
${\beta })$
be a root of
$x^p-x = Q_i/P_i^{r_i}$
for
$1 \leq i \leq m\ ($
resp.
$x^p-x = f(T))$
in
$\overline {k}$
. Then the genus field
$\mathcal {G}_{K}$
of K is
$\mathcal {G}_{K} = k({\alpha }_1, \dots , {\alpha }_m, {\beta }).$
We now introduce explicit criteria for determining whether a place of k is totally ramified or not in the Artin–Schreier extension K.
Lemma 2.4 [Reference Stichtenoth18, Proposition 3.7.8]
Let
$K=k(y)$
be the Artin–Schreier extension over k of extension degree p, where
$y^p-y=u$
for some
$u \in k$
. For a place P of k, we define the integer
$m_P$
by
$$ \begin{align*}m_P := \left\{ \begin{array}{ll} m, & \mbox{if there is an element}\ z \in k\ \mbox{satisfying} \\ & \upsilon_P(u-(z^p-z)) = -m < 0\ \mbox{and}\ m \not \equiv 0\quad \pmod p, \\ -1, & \mbox{if}\ \upsilon_P(u-(z^p-z)) \geq 0\ \mbox{for some}\ z \in k. \end{array} \right.\end{align*} $$
Then we have the followings.
-
(i) P is totally ramified in
$K/k$
if and only if
$m_P> 0$
. -
(ii) P is unramified in
$K/k$
if and only if
$m_P = -1$
.
Lemma 2.5 [Reference Rosen17, Proposition 14.1]
Let K be a function field over the rational function field
$k={\mathbb F}_q(T)$
, and let
$\infty $
be the infinite place of k. Denote the ideal class group (resp. the divisor class group) of K by
$Cl_K$
(resp.
$J_K$
) and S be a set of places of K lying over
$\infty $
. Then
$$ \begin{align*}0 \rightarrow \mathcal{D}^0_K(S)/\mathcal{P}_K(S) \rightarrow J_K \rightarrow Cl_K \rightarrow {\mathbb Z}/d{\mathbb Z} \rightarrow 0\end{align*} $$
is an exact sequence, where
$\mathcal {D}_K^{0}(S)$
is the divisor group with support only in S whose degree is zero,
$\mathcal {P}_K(S)$
is a principal divisor with support only in S, and d is the greatest common divisor of the elements in
$\{\deg P : P \in S \}$
.
Using Lemma 2.5, we can easily obtain the following corollary, which gives relation between the ideal class group of K and the divisor class group of K, where K is the Artin–Schreier function field over k.
Lemma 2.6 Let K be the Artin–Schreier extension over k with extension degree p, and let all the notations be the same as in Lemma 2.5. Then we have the following.
-
(i) If
$\infty $
is totally ramified in K, then
$\mathcal {D}_K^0(S)$
is trivial and
$d = 1$
; thus, is exact.
$$ \begin{align*}0 \rightarrow J_K \rightarrow Cl_K \rightarrow 0\end{align*} $$
-
(ii) If
$\infty $
is inert in K, then
$\mathcal {D}_K^0(S)$
is trivial and
$d = p$
; therefore, is an exact sequence.
$$ \begin{align*}0 \rightarrow J_K \rightarrow Cl_K \rightarrow {\mathbb Z}/p{\mathbb Z} \rightarrow 0\end{align*} $$
-
(iii) If
$\infty $
splits completely in K, then
$d = 1$
; thus, is exact.
$$ \begin{align*}0 \rightarrow \mathcal{D}_K^{0}(S)/\mathcal{P}_K(S) \rightarrow J_K \rightarrow Cl_K \rightarrow 0\end{align*} $$
3 Infinite families of Artin–Schreier function fields with any prescribed class group
${\lambda }$
-rank
In this section, for any positive integer t, we find infinite families of Artin–Schreier function fields K over k whose
${\lambda }$
-rank of the ideal class group
$Cl_K$
of K is t and
${\lambda }_n$
-rank of
$Cl_K$
is zero for
$n \ge 2$
, depending on the ramification behavior of the infinite place
$\infty $
of k. Theorem 3.2 deals with the case where the infinite place
$\infty $
of k is totally ramified in K and Theorem 3.3 (resp. Theorem 3.4) treats the case where the infinite place
$\infty $
of k splits completely (resp.
$\infty $
is inert) in K.
We first give the following lemma, which shows the property of the trace over finite fields. This lemma plays a key role in the proofs of Theorems 3.2–3.4.
Lemma 3.1 Let h be a monic irreducible polynomial in
${\mathbb F}_q[T]$
and
$\mathfrak {h} := q^{\deg h}$
. Let g be a nonzero element in
${\mathbb F}_q[T]$
, and let
$\tilde {g} \in {\mathbb F}_{\mathfrak {h}}$
be
$\phi \circ \pi (g)$
, where
$$ \begin{align*}g \in {\mathbb F}_q[T] \xrightarrow{\hspace{0.2cm}\pi\hspace{0.2cm}} \pi(g) \in {\mathbb F}_q[T]/{\langle} h {\rangle} \xrightarrow{\hspace{0.2cm}\phi\hspace{0.2cm}} {\mathbb F}_{\mathfrak{h}}.\end{align*} $$
Then we have
$\operatorname {\mathrm {Tr}}_{{\mathbb F}_{\mathfrak {h}}/{\mathbb F}_q} \widetilde {g} = 0$
if and only if the following holds:
-
(i) If
$\deg g =0$
, then
$q \mid \deg h$
. -
(ii) If
$\deg g \geq 1$
, then
$g \equiv b(T)^q-b(T)\ \pmod {h}$
for some
$b(T) \in {\mathbb F}_q[T]$
.
Proof We note that
${\mathbb F}_{\mathfrak {h}} \simeq {\mathbb F}_q[T]/{\langle } h {\rangle }$
since h is an irreducible polynomial over
${\mathbb F}_q$
.
First, assume that
$\deg g = 0$
: that is, g is an element of
${\mathbb F}_q^\times $
, and so
$g = \tilde {g}$
. Then we have the following:
$$ \begin{align*}\operatorname{\mathrm{Tr}}_{{\mathbb F}_{\mathfrak{h}}/{\mathbb F}_q} \tilde{g} = 0 \text{ if and only if } q \mid \deg h;\end{align*} $$
this is because
$\operatorname {\mathrm {Tr}}_{{\mathbb F}_{\mathfrak {h}}/{\mathbb F}_q} \tilde {g} = \tilde {g}\cdot \deg h$
in
${\mathbb F}_q$
.
Now, we consider the case where
$\deg g \geq 1$
. Assume that
$g \equiv b(T)^q-b(T)\ \pmod h$
. Then we have
$$ \begin{align*}\tilde{g} = \phi \circ \pi (g) = \phi ((b(T))^q-(b(T))) = \phi(b(T))^q - \phi (b(T)) = \tilde{b}^q - \tilde{b},\end{align*} $$
where
$\tilde {b} := \phi (b(T)) \in {\mathbb F}_{\mathfrak {h}}$
. Therefore, the result follows immediately by [Reference Lidl and Niederreiter12, Theorem 2.25]. Conversely, now assume that
$\operatorname {\mathrm {Tr}}_{{\mathbb F}_{\mathfrak {h}/{\mathbb F}_q}}(\tilde {g}) = 0$
: that is, there exists some
$\tilde {b}\in {\mathbb F}_{\mathfrak {h}}$
such that
$\tilde {g} = \tilde {b}^q - \tilde {b}$
. Let
$b(T) := \phi ^{-1}(\tilde {b})$
; there exists such
$b(T) \in {\mathbb F}_q[T]$
since
$\phi $
is isomorphism. Thus, we get
$$ \begin{align*}g= \pi^{-1} \circ \phi^{-1}(\tilde{g}) = \pi^{-1} \circ \phi^{-1}(\tilde{b}^q - \tilde{b}) = \pi^{-1}((b(T))^q-(b(T)));\end{align*} $$
this implies that
$g \equiv b(T)^q - b(T)\ \pmod h$
.
Theorem 3.2 Let t be a positive integer. Let
be the Artin–Schreier extension over the rational function field
$k = {\mathbb F}_q(T)$
of extension degree p, where
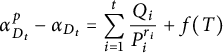
satisfies (2.1). Assume that the infinite place
$\infty $
of k is totally ramified in K; equivalently,
$\deg f(T) \ge 1$
with
$p \nmid \deg f(T)$
. We further assume that the followings hold:
-
(i)
$p \nmid \deg P_i$
for any i with
$1 \leq i \leq t$
. -
(ii)
$f(T) \equiv \mathfrak {c}_i\ \pmod {P_i}$
, where
$\mathfrak {c}_i \in {\mathbb F}_q^\times $
such that
$\operatorname {\mathrm {Tr}}_{{\mathbb F}_q/{\mathbb F}_p}(\mathfrak {c}_i) \ne 0$
for any i with
$1 \leq i \leq t$
. -
(iii)
$Q_j \equiv {P_j}^{r_j}(b_i(T)^q-b_i(T))\ \pmod {P_i}$
for any i with
$1 \leq i \ne j \leq t$
, where
$b_i(T)$
is a polynomial in
${\mathbb F}_q[T]$
.
Then the
${\lambda }_1$
-rank of the ideal class group
$Cl_K$
of K and
${\mu }_1$
-rank of the divisor class group
$J_K$
of K are t. Moreover, for
$n \ge 2$
, the
${\lambda }_n$
-rank of
$Cl_K$
and the
${\mu }_n$
-rank of
$J_K$
are zero.
In particular, for the case when
$p=2$
, the
$2$
-class groups
$Cl_K(2)$
and
$J_K(2)$
are elementary abelian
$2$
-groups: that is, isomorphic to
$({\mathbb Z}/2{\mathbb Z})^{t}$
.
Proof We note that by Lemma 2.6, the ideal class group of K and the divisor class group of K are isomorphic; thus,
${\lambda }_n = {\mu }_n$
for
$n \ge 1$
. Since
${\lambda }_n$
is a decreasing sequence as n grows (
${\lambda }_{n-1}$
and
${\lambda }_n$
may have the same value), it suffices to show the following:
$$ \begin{align} {\lambda}_1 = t \quad \mbox{and} \quad {\lambda}_2 = 0. \end{align} $$
By Lemma 2.2, we can easily get
${\lambda }_1 = t$
. Thus, we will show that the rank of R is t, where R is the Rédei matrix over
${\mathbb F}_p$
which is defined in Lemma 2.2.
Let
$f(T)$
be a polynomial in
${\mathbb F}_q[T]$
which satisfies condition (ii). For convenience, let
${\delta }_i:=\deg P_i$
for
$1 \leq i \leq t$
. Then we have the following:
$$ \begin{align*}\operatorname{\mathrm{Tr}}_{{\mathbb F}_{q^{{\delta}_i}}/{\mathbb F}_q}(f\quad \pmod {P_i}) = \operatorname{\mathrm{Tr}}_{{\mathbb F}_{q^{{\delta}_i}}/{\mathbb F}_q} \mathfrak{c}_i = {\delta}_i \mathfrak{c}_i;\end{align*} $$
the last equality follows from the fact that
$\mathfrak {c}_i \in {\mathbb F}_q^\times $
. Thus, by the definition of the Hasse symbol, we obtain
$$ \begin{align} \left\{ \frac{f(T)}{P_i} \right\} = \operatorname{\mathrm{Tr}}_{{\mathbb F}_q/{\mathbb F}_p} (\operatorname{\mathrm{Tr}}_{{\mathbb F}_{q^{{\delta}_i}}/{\mathbb F}_q} (f\quad \pmod {P_i})) = \operatorname{\mathrm{Tr}}_{{\mathbb F}_q/{\mathbb F}_p} ({\delta}_i\mathfrak{c}_i) = {\delta}_i\operatorname{\mathrm{Tr}}_{{\mathbb F}_q/{\mathbb F}_p} \mathfrak{c}_i \ne 0; \end{align} $$
for the last equality, we use conditions (i) and (ii).
Now, let
$Q_j$
(
$1 \leq j \leq t$
) be a polynomial in
${\mathbb F}_q[T]$
which satisfies condition (iii). Then, for
$1 \leq i \ne j \leq t$
, we have
$$ \begin{align*}Q_j{\overline{P_j}}^{r_j} \equiv b_i(T)^q - b_i(T)\quad \pmod {P_i},\end{align*} $$
where
$P_j\overline {P_j} \equiv 1\ \pmod {P_i}$
. We note that
$\overline {P_j}$
always exist since
$P_i$
and
$P_j$
are relative prime in
${\mathbb F}_q[T]$
. Then, by Lemma 3.1, we obtain
$\operatorname {\mathrm {Tr}}_{{\mathbb F}_{{\delta }_i}/{\mathbb F}_q} (Q_j{\overline {P_j}}^{r_j}\ \pmod {P_i}) = 0$
, where
${\delta }_i:=\deg P_i$
. Thus, we obtain
$$ \begin{align} \left\{ \frac{Q_j/{P_j}^{r_j}}{P_i} \right\} = \operatorname{\mathrm{Tr}}_{{\mathbb F}_q/{\mathbb F}_p}(\operatorname{\mathrm{Tr}}_{{\mathbb F}_{q^{{\delta}_i}}/{\mathbb F}_q} (Q_j\overline{P_j}^{r_j}\quad \pmod {P_i}) = \operatorname{\mathrm{Tr}}_{{\mathbb F}_q/{\mathbb F}_p} 0 = 0. \end{align} $$
Therefore, we get a
$t \times t$
Rédei matrix
$R = [r_{ij}]$
over
${\mathbb F}_p$
as follows:
$$ \begin{align} {\small{R = \left[ \begin{array}{cccc} r_{11} & 0 & \cdots & 0\\ 0 & r_{22} & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0& \cdots & r_{tt} \\ \end{array} \right]}}, \end{align} $$
where
$r_{ii} = \left \{ \frac {f(T)}{P_i} \right \} \ne 0$
in
${\mathbb F}_p$
for every
$1 \leq i \leq t$
. We can easily check that the rank of R is t; therefore, we get
${\lambda }_2 = {\lambda }_1 - \operatorname {\mathrm {rank}}(R) = 0$
.
For the case where
$p=2$
, the
$2^n$
-rank of
$Cl_K$
and that of
$J_K$
are exactly
$\lambda _n$
and
${\mu }_n$
, respectively; therefore,
$Cl_K(2) \simeq J_K(2) \simeq ({\mathbb Z}/2{\mathbb Z})^t$
.
Theorem 3.3 Let t be a positive integer. Let
be the Artin–Schreier extension over the rational function field
$k = {\mathbb F}_q(T)$
of extension degree p, where
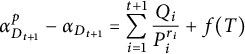
satisfies (2.1). Assume that the infinite place
$\infty $
splits completely in K; equivalently,
$f(T)=0$
. We further assume that the followings hold:
-
(i)
$p \nmid \deg P_i$
for any i with
$1 \leq i \leq t+1$
. -
(ii)
$Q_t \equiv \mathfrak {c}_iP_t^{r_t}\ \pmod {P_i}$
, where
$\mathfrak {c}_i \in {\mathbb F}_q^\times $
such that
$\operatorname {\mathrm {Tr}}_{{\mathbb F}_q/{\mathbb F}_p}(\mathfrak {c}_i) \ne 0$
for any i with
${1 \leq i \leq t}$
. -
(iii)
$Q_j \equiv P_j^{r_j}(b_i(T)^q-b_i(T))\ \pmod {P_i}$
for any
$1 \leq i \leq t+1$
,
$1 \leq j \leq t$
,
$i \ne j$
, where
$b_i(T) \in {\mathbb F}_q[T]$
.
Then the
${\lambda }_1$
-rank of the ideal class group
$Cl_K$
of K is t. Moreover, for
$n \ge 2$
, the
${\lambda }_n$
-rank of
$Cl_K$
is zero.
In particular, for the case when
$p=2$
, the
$2$
-class group
$Cl_K(2)$
is an elementary abelian
$2$
-group: that is, isomorphic to
$({\mathbb Z}/2{\mathbb Z})^{t}$
.
Proof As in Theorem 3.2, we will show (3.1). The fact that
${\lambda }_1 = t$
comes immediately from Lemma 2.2. Thus, it is sufficient to show that
$\lambda _2=0$
: that is,
$\operatorname {\mathrm {rank}}(R) = {\lambda }_1 = t$
, where R is the Rédei matrix of K defined in Lemma 2.2.
Let
$D_i:=\frac {Q_i}{P_i^{r_i}}$
for
$1 \leq i \leq t+1$
. Using the same reasoning as in Theorem 3.2, we get
$\left \{D_t/P_i \right \} \ne 0$
for every
$1 \leq i \leq t$
; we note that we use conditions (i) and (ii). Thus, the
$i(t+1)$
th entry of R is nonzero for
$1 \leq i \leq t$
. By condition (iii), we obtain
$\left \{ D_j/ P_i \right \} =0$
from Lemma 3.1; this implies that the
$ij$
th entries of R are all zero for
$1 \leq i \leq t+1$
and
$1 \leq j \leq t$
with
$i \ne j$
.
Therefore, we obtain a
$(t+1) \times (t+1)$
matrix
$R = [r_{ij}]$
over
${\mathbb F}_p$
as follows:
$$ \begin{align*}{\small{R = \left[ \begin{array}{ccccl} -r_{1,t+1} & 0 & \cdots & 0 & r_{1,t+1}\\ 0 & -r_{2,t+1} & \cdots & 0 & r_{2,t+1}\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0& \cdots & -r_{t,t+1} & r_{t,t+1}\\ 0 & 0 & \cdots & 0 & 0 \\ \end{array} \right]}},\end{align*} $$
where
$r_{i,t+1} \ne 0$
in
${\mathbb F}_p$
for every
$1 \leq i \leq t$
. Thus, the result follows immediately.
For the case where
$p=2$
, since
${\lambda }_n$
gives the full
$2^n$
-rank of
$Cl_K$
, we obtain that
$Cl_K(2) \simeq ({\mathbb Z}/2{\mathbb Z})^t$
.
Theorem 3.4 Let t be a positive integer. Let
be the Artin–Schreier extension over the rational function field
$k = {\mathbb F}_q(T)$
of extension degree p, where
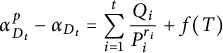
satisfies (2.1). Assume that
$\infty $
is inert in K; equivalently,
$f(T) = c \in {\mathbb F}_q^\times $
, where
$x^p-x-c$
is irreducible over
${\mathbb F}_q$
. We further assume that the followings hold: for some
$\mathfrak {c} \in {\mathbb F}_q$
,
-
(i)
$p \nmid \deg {P_i}$
for every
$1 \leq i \leq t$
. -
(ii)
$Q_j \equiv P_j^{r_j}(b_i(T)^q-b_i(T))$
for any i with
$1 \leq i \ne j \leq t$
, where
$b_i(T) \in {\mathbb F}_q[T]$
.
Then the
${\lambda }_1$
-rank of the ideal class group
$Cl_K$
of K is t. Moreover, for
$n \ge 2$
, the
${\lambda }_n$
-rank of
$Cl_K$
is zero.
In particular, for the case when
$p=2$
, then
$Cl_K(2)$
is isomorphic to
$({\mathbb Z}/2{\mathbb Z})^t$
and
$J_K(2)$
is isomorphic to
$({\mathbb Z}/2{\mathbb Z})^{t-1}$
.
Proof We can simply get
${\lambda }_1 = t$
by Lemma 2.2; we now show that
${\lambda }_2 = 0$
, which implies that the rank of the Rédei matrix R is t. As usual, set
$D_i:=\frac {Q_i}{P_i^{r_i}}$
. Using Lemma 3.1, we obtain
$\left \{ D_j/ P_i \right \} = 0$
for every
$1 \leq i \ne j \leq t$
. Now, we compute
$\left \{ c/P_i\right \}$
for
$1 \leq i \leq t$
, where
$c \in {\mathbb F}_q^\times $
. Let
${\delta }_{i}$
be the degree of
$P_i$
. By the definition of Hasse norm, we have
$$ \begin{align} \left\{ \frac{c}{P_i} \right\} &=& \operatorname{\mathrm{Tr}}_{{\mathbb F}_q/{\mathbb F}_p} \operatorname{\mathrm{Tr}}_{{{\mathbb F}_q^{{\delta}_i}}/{\mathbb F}_q}(c\quad \pmod {P_i}) = \operatorname{\mathrm{Tr}}_{{\mathbb F}_{q}/{\mathbb F}_p} ({\delta}_i c) = {\delta}_i\operatorname{\mathrm{Tr}}_{{\mathbb F}_q/{\mathbb F}_p} (c). \end{align} $$
We note that
$\operatorname {\mathrm {Tr}}_{{\mathbb F}_q/{\mathbb F}_p}(c) \ne 0$
since
$x^p-x-c$
is irreducible over
${\mathbb F}_q$
. Therefore, (3.5) is nonzero; we use condition (i). Using the definition of the Rédei matrix R in Lemma 2.2, we get a
$t \times t$
matrix
$R = [r_{ij}]$
over
${\mathbb F}_p$
which is given in (3.4). Hence, the desired result follows.
For the case where
$p=2$
, the 2-class group of
$Cl_K$
is isomorphic to
$({\mathbb Z}/2{\mathbb Z})^t$
by the fact that
${\lambda }_n$
gives the full
$2^n$
-rank of
$Cl_K$
. By Lemma 2.6, the remaining result follows.
4 Computing the
${\lambda }_3$
-rank of class groups of Artin–Schreier function fields
In this section, Algorithm 1 presents an explicit method for computing the
${\lambda }_3$
-rank of the ideal class groups of Artin–Schreier extensions K over k. In Theorem 4.3, we provide a proof for Algorithm 1. In particular, we obtain an explicit method for determining the exact
$2^3$
-rank of the ideal class groups of Artin–Schreier quadratic extensions over k (Corollary 4.4).
The following lemma plays a crucial role for the proof of Theorem 4.3.
Lemma 4.1 Let
be the Artin–Schreier extension over k of extension degree p, where
$D_m(T) = \sum _{i=1}^{m} \frac {Q_i}{P_i^{r_i}} + f(T)$
is defined as (2.1) and
is a root of
$x^p-x = D_m$
. For
$1 \leq i \leq m$
, let
${\alpha }_i$
be a root of
$x^p-x = D_i := Q_i/P_i^{r_i}$
and let
${\gamma }_i$
be a root of the following equation in
$\overline {k}$
:
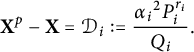$$ \begin{align*} \mathbf{X}^p-\mathbf{X} = \mathcal{D}_i := \frac{{{\alpha}_i}^2 P_i^{r_i}}{Q_i}. \end{align*} $$
Then
$k({\alpha }_i,{\gamma }_i)/k({\alpha }_i)$
is unramified, where all the infinite places of
$k({\alpha }_i)$
split completely in
$k({\alpha }_i, {\gamma }_i)$
.
Proof We first show that
$k({\alpha }_i, {\gamma }_i)/k({\alpha }_i)$
is an unramified extension. Let
${\mathfrak p}_i \in k({\alpha }_i)$
be a place which lies above a finite place P of k. We note that it suffices to show the following by Lemma 2.4:
$$ \begin{align} v_{{\mathfrak p}_i}(\mathcal{D}_i) = 2v_{{\mathfrak p}_i}({\alpha}_i) + v_{{\mathfrak p}_i}(P_i^{r_i})-v_{{\mathfrak p}_i}(Q_i) \geq 0. \end{align} $$
We consider the following three possible cases:
$P = P_i$
for
$1 \leq i \leq m$
, P divides
$Q_i \in {\mathbb F}_q[T]$
, and
$(P, P_i)=(P,Q_i)=1$
. Using a valuation property, we can easily show the following, where n is a positive integer.
$$ \begin{align} &\mbox{If}\ v_{{\mathfrak p}_i}({\alpha}_i^n-{\alpha}_i) < 0,\ \mbox{then}\ v_{{\mathfrak p}_i}({\alpha}_i^n-{\alpha}_i) = nv_{{\mathfrak p}_i}({\alpha}_i) < 0. \end{align} $$
$$ \begin{align} &\mbox{If}\ v_{{\mathfrak p}_i}({\alpha}_i^n-{\alpha}_i)> 0,\ \mbox{then}\ v_{{\mathfrak p}_i}({\alpha}_i) \geq 0.\qquad\qquad\qquad\ \ \end{align} $$
$$ \begin{align} &\!\!\!\mbox{If}\ v_{{\mathfrak p}_i}({\alpha}_i^n-{\alpha}_i) = 0,\ \mbox{then}\ v_{{\mathfrak p}_i}({\alpha}_i^n-{\alpha}_i) = v_{{\mathfrak p}_i}({\alpha}_i) = 0. \end{align} $$
We denote the ramification index of
$\mathfrak {p}_i$
over P in
$k({\alpha }_i)/k$
by
$e(\mathfrak {p}_i|P)$
and the residue class field degree of
$\mathfrak {p}_i$
over P by
$f(\mathfrak {p}_i|P)$
.
(i) Suppose that
$P = P_i$
. Then we have
$e({{\mathfrak p}_i}|P) = e({{\mathfrak p}_i}|P_i) = p$
since
$P_i$
is the only totally ramified finite place for
$k({\alpha }_i)/k$
. Therefore, we have
$v_{{\mathfrak p}_i}({\alpha }_i^p-{\alpha }_i) = v_{{\mathfrak p}_i}(Q_i/P_i^{r_i}) = -pr_i < 0$
; this implies that
$v_{{\mathfrak p}_i}({\alpha }_i) = -r_i$
by (4.2). Therefore, (4.1) holds true.
(ii) Suppose that P divides
$Q_i$
in
${\mathbb F}_q[T]$
. Under the given assumption, we have
$e({{\mathfrak p}_i}|P) = 1$
; this is because
$(P,P_i) = 1$
as
$(P_i, Q_i)=1$
and
$P_i$
is the only totally ramified finite place for
$k({\alpha }_i)/k$
. Consequently, we have
$$ \begin{align*}v_{{{\mathfrak p}_i}}({\alpha}_i^p-{\alpha}_i) = v_{{{\mathfrak p}_i}}(Q_i/P_i^{r_i}) = v_{P}(Q_i/P_i^{r_i}) = v_P(Q_i)> 0;\end{align*} $$
thus,
$v_{{{\mathfrak p}_i}}({\alpha }_i) \geq 0$
by (4.3). Assuming that
$v_{{{\mathfrak p}_i}}({\alpha }_i)=0$
, we obtain
$$ \begin{align} v_{P}(N_{k({\alpha}_i)/k} ({\alpha}_i)) = f({{\mathfrak p}_i}|P)v_{{{\mathfrak p}_i}}({\alpha}_i) = 0. \end{align} $$
However, since
$v_{{{\mathfrak p}_i}}(N_{k({\alpha }_i)/k} ({\alpha }_i)) = v_{{\mathfrak p}_i}(Q_i/P_i^{r_i})>0$
(4.5) cannot happen. Therefore, we have
$v_{{\mathfrak p}_i}(\mathcal {D}_i) = 2v_P(Q_i) - v_P(Q_i)> 0$
and (4.1) follows; we use the fact that
$v_{{\mathfrak p}_i}({\alpha }_i) = v_P(Q_i)> 0$
. As a result,
${{\mathfrak p}_i}$
is unramified in
$k({\alpha }_i,{\gamma }_i)$
.
(iii) Suppose that
$(P,P_i) = (P,Q_i)= 1$
. In this case, we get
$v_{{\mathfrak p}_i}({\alpha }_i) = 0$
by (4.4) since
$v_{{\mathfrak p}_i}({\alpha }_i^p-{\alpha }_i)=0$
. Therefore, (4.1) follows immediately.
Now, it remains to show that all the infinite places of
$k({\alpha }_i)$
split completely in
$k({\alpha }_i,{\gamma }_i)$
. Let
${\mathfrak p}_{\infty }$
(resp.
${\mathfrak P}_{\infty }$
) be a place of
$k({\alpha }_i)$
(resp.
$k({\alpha }_i, {\gamma }_i)$
) lying above the infinite place
${\infty }$
of k (resp.
${\mathfrak p}_{\infty }$
). We first note that
$v_{{\mathfrak p}_{\infty }}({\alpha }_i^p-{\alpha }_i) = v_{{\mathfrak p}_{\infty }}(Q_i/P_i^{r_i})> 0$
; thus,
$v_{{\mathfrak p}_{\infty }}({\alpha }_i)\geq 0$
by (4.3). By a similar computation method as in (4.5), we obtain
$v_{{\mathfrak p}_{\infty }}({\alpha }_i)> 0$
, and therefore
$v_{{\mathfrak p}_{\infty }}({\alpha }_i) = v_{{\mathfrak p}_{\infty }}({\alpha }_i^p-{\alpha }_i) = \deg {P_i^{r_i}} - \deg {Q_i}$
. Hence, we get
$$ \begin{align*}v_{{\mathfrak p}_{\infty}}(\mathcal{D}_i) = 2v_{{\mathfrak p}_{\infty}}({\alpha}_i) + v_{{\mathfrak p}_{\infty}}(P_i^{r_i})-v_{{\mathfrak p}_{\infty}}(Q_i) = 2(\deg{P_i^{r_i}} - \deg {Q_i}) - \deg{P_i^{r_i}} + \deg {Q_i}> 0;\end{align*} $$
from this fact and by Lemma 2.4, we can conclude that
${\mathfrak p}_{\infty }$
is unramified in
$k({\alpha }_i,{\gamma }_i)/k({\alpha }_i)$
.
Now, it is enough to show that
$f({\mathfrak P}_{\infty }|{\mathfrak p}_{\infty })$
is 1. For the proof, we assume that
$f({\mathfrak P}_{\infty }|{\mathfrak p}_{\infty }) = p$
. We first note that
$$ \begin{align} N_{k({\alpha}_i,{\gamma}_i)/k({\alpha}_i)}({\gamma}_i) = {\gamma}_i^p-{\gamma}_i = {\alpha}_i^2P_i^{r_i}/Q_i. \end{align} $$
On the other hand, we have
$$ \begin{align} v_{{\mathfrak p}_{\infty}}(N_{k({\alpha}_i,{\gamma}_i)/k({\alpha}_i)} ({\gamma}_i)) = f({\mathfrak P}_{\infty}|{\mathfrak p}_{\infty})v_{{\mathfrak P}_{\infty}}({\gamma}_i) = pv_{{\mathfrak P}_{\infty}}({\gamma}_i). \end{align} $$
Also, we can obtain
$$ \begin{align} pv_{{\mathfrak P}_{\infty}}({\gamma}_i) = v_{{\mathfrak p}_{\infty}}({\gamma}_i^p-{\gamma}_i) = v_{{\mathfrak P}_{\infty}}({\gamma}_i^p-{\gamma}_i), \end{align} $$
by combining (4.6) with (4.7). Furthermore, since
$v_{{\mathfrak p}_{\infty }}({\gamma }_i^p-{\gamma }_i) = pv_{{\mathfrak P}_{\infty }}({\gamma }_i)> 0$
, we have
$$ \begin{align} pv_{{\mathfrak P}_{\infty}}({\gamma}_i) = \min\{pv_{{\mathfrak P}_{\infty}}({\gamma}_i) ,v_{{\mathfrak P}_{\infty}}({\gamma}_i)\} = v_{{\mathfrak P}_{\infty}}({\gamma}_i), \end{align} $$
which is a contradiction. Therefore, the infinite place of
$k({\alpha }_i)$
splits completely in
$k({\alpha }_i,{\gamma }_i)$
.
Lemma 4.2 Let K be the Artin–Schreier extension over k of extension degree p. Let
$H_{K}$
be the Hilbert class field of K, and let
$\mathcal {G}_{K}$
be the genus field of
${K}$
. Let
$\mathcal {H}$
be a fixed field of a subgroup of
$\mathrm{Gal}(H_K/\mathcal {G}_K)$
which is isomorphic to
$Cl_K^{({\sigma }-1)^2}$
. Then
$Cl_{K}(p)^{({\sigma }-1)}/Cl_{K}(p)^{({\sigma }-1)^{2}}$
is isomorphic to
$\mathrm{Gal}(\mathcal {H}/\mathcal {G}_{K})$
; thus, we can define the following composite map:
$$ \begin{align} \Psi: Cl_{K}(p)^G \cap Cl_{K}(p)^{({\sigma}-1)} \rightarrow Cl_{K}(p)^{({\sigma}-1)}/Cl_{K}(p)^{({\sigma}-1)^{2}} \xrightarrow{\simeq} \mathrm{Gal}(\mathcal{H}/\mathcal{G}_{K}), \end{align} $$
where the first map is induced by the inclusion map.
Then
${\lambda }_3$
is equal to
${\lambda }_2-\operatorname {\mathrm {rank}}(\mathcal {R})$
, where
$\mathcal {R}$
is a matrix representing
$\Psi $
over
${\mathbb F}_p$
and
${\lambda }_2$
is obtained by Lemma 2.2.
Proof We note that
$\mathrm{Gal}(H_K/K) \simeq Cl_K$
and
$\mathrm{Gal}(\mathcal {G}_K/K) \simeq Cl_K(p)/Cl_K(p)^{({\sigma }-1)} \simeq Cl_K/Cl_K^{({\sigma }-1)}$
[Reference Wittmann19, pp. 328–329]; therefore,
$\mathrm{Gal}(H_K/\mathcal {G}_K) \simeq Cl_K^{({\sigma }-1)}$
. By the Galois correspondence, we have isomorphisms
$\mathrm{Gal}(\mathcal {H}/\mathcal {G}_K) \simeq Cl_K^{({\sigma }-1)}/Cl_K^{({\sigma }-1)^2}$
and
$Cl_K^{({\sigma }-1)}/Cl_K^{({\sigma }-1)^2} \simeq Cl_K(p)^{({\sigma }-1)}/Cl_K(p)^{({\sigma }-1)^2}$
; thus, we have the isomorphism
$Cl_K(p)^{({\sigma }-1)}/Cl_K(p)^{({\sigma }-1)^2} \xrightarrow {\simeq } \operatorname {\mathrm {Gal}}(\mathcal {H}/\mathcal {G}_K)$
.
Let
$\Psi $
be the map defined as in (4.10). Then we have
$$ \begin{align*} |\operatorname{\mathrm{Ker}} (\Psi)| = |Cl_K(p)^G \cap Cl_K(p)^{({\sigma}-1)^2}|. \end{align*} $$
We claim that for any positive integer n,
$$ \begin{align} |Cl_K(p)^G \cap Cl_K(p)^{({\sigma}-1)^{n-1}}| = |Cl_K(p)^{({\sigma}-1)^{n-1}}/Cl_K(p)^{({\sigma}-1)^{n}}|. \end{align} $$
We consider a short exact sequence
$$ \begin{align*}0 \rightarrow Cl_K(p)^G \cap Cl_K(p)^{({\sigma}-1)^{n-1}} \xrightarrow{\imath} Cl_K(p)^{({\sigma}-1)^{n-1}} \xrightarrow{{\sigma}-1} Cl_K(p)^{({\sigma}-1)^{n}} \rightarrow 0,\end{align*} $$
where
$\imath $
denotes an inclusion map. Then
$Cl_K(p)^{({\sigma }-1)^n}$
is isomorphic to
$$ \begin{align*}Cl_K(p)^{({\sigma}-1)^{n-1}}/\mbox{Im}(\imath) = Cl_K(p)^{({\sigma}-1)^{n-1}} / Cl_K(p)^G \cap Cl_K(p)^{({\sigma}-1)^{n-1}}.\end{align*} $$
Therefore, we have the following:
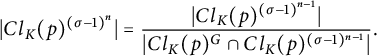$$ \begin{align*} |Cl_K(p)^{({\sigma}-1)^n}| = \frac{|Cl_K(p)^{({\sigma}-1)^{n-1}}|}{|Cl_K(p)^G \cap Cl_K(p)^{({\sigma}-1)^{n-1}}|}. \end{align*} $$
We can rewrite this as
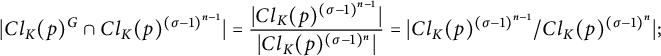$$ \begin{align*} |Cl_K(p)^G \cap Cl_K(p)^{({\sigma}-1)^{n-1}}| = \frac{|Cl_K(p)^{({\sigma}-1)^{n-1}}|}{|Cl_K(p)^{({\sigma}-1)^{n}}|} = |Cl_K(p)^{({\sigma}-1)^{n-1}}/Cl_K(p)^{({\sigma}-1)^{n}}|; \end{align*} $$
hence, (4.11) follows.
Therefore, we compute as follows:
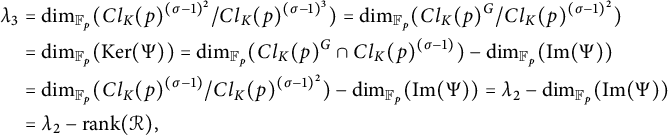$$ \begin{align*} {\lambda}_3 &= \mbox{dim}_{{\mathbb F}_p}(Cl_K(p)^{({\sigma}-1)^{2}}/Cl_K(p)^{({\sigma}-1)^{3}}) = \dim_{{\mathbb F}_p}(Cl_K(p)^{G}/Cl_K(p)^{({\sigma}-1)^{2}})\\ &= \dim_{{\mathbb F}_p}(\operatorname{\mathrm{Ker}}(\Psi)) = \dim_{{\mathbb F}_p}(Cl_K(p)^G \cap Cl_K(p)^{{({\sigma}-1)}}) - \dim_{{\mathbb F}_p}(\mbox{Im} (\Psi))\\ &= \dim_{{\mathbb F}_p}(Cl_K(p)^{({\sigma}-1)}/Cl_K(p)^{({\sigma}-1)^{2}}) - \dim_{{\mathbb F}_p}(\mbox{Im} (\Psi)) = {\lambda}_2 - \dim_{{\mathbb F}_p}(\mbox{Im} (\Psi))\\ &= {\lambda}_2 - \mbox{rank}(\mathcal{R}), \end{align*} $$
where
$\mathcal {R}$
is a matrix representing
$\Psi $
over
${\mathbb F}_p$
and
${\lambda }_2$
is obtained by Lemma 2.2. We note that the second equality and the fifth one hold by (4.11) with
$n =3$
and 2, respectively.
Theorem 4.3 Let K be the Artin–Schreier extension over the rational function field k of extension degree p. Then the
${\lambda }_3$
-rank of the ideal class group of K can be computed by Algorithm 1.
Proof By Lemma 4.2, we have
${\lambda }_3 = {\lambda }_2 - \operatorname {\mathrm {rank}}(\mathcal {R})$
, where
$\mathcal {R}$
is a matrix representing
$\Psi $
which is defined as in (4.10). Therefore, it is sufficient to compute the matrix
$\mathcal {R}$
in an explicit way for computation of
${\lambda }_3$
. We describe how to compute the matrix
$\mathcal {R}$
as follows.
Let
$\mathcal {I}:=\{1 \leq i \leq m \mid \mbox {the}\ i\mbox {th row vector of}\ R\ \mbox {is zero}\} = \{s_1, \ldots , s_{{\lambda }_2}\}$
, where
$s_i < s_j$
for
$1 \leq i < j \leq {\lambda }_2$
. For simplicity, we set
$\mathcal {P}_i:=P_{s_i}$
and
$\mathcal {F}_i = Q_{s_i}/P_{s_i}^{r_{s_i}}$
for
$1 \leq i \leq {\lambda }_2$
. Let
$\mathcal {D}_i := {\mathfrak {a}_i}^2/\mathcal {F}_i$
, and let
${\gamma }_i$
be a root of
$\mathbf {X}^p - \mathbf {X} = \mathcal {D}_i$
in
$\overline {k}$
, where
$\overline {k}$
is the algebraic closure of k and
$\mathfrak {a}_i$
is the root of
$x^p-x = \mathcal {F}_i$
in
$\overline {k}$
.
Let
$L:= k({\alpha }_1, \ldots , {\alpha }_m)$
be a subfield of the genus field
$\mathcal {G}_{K}$
defined as the following, where
$\mathcal {G}_{K}$
is given in Lemma 2.3.
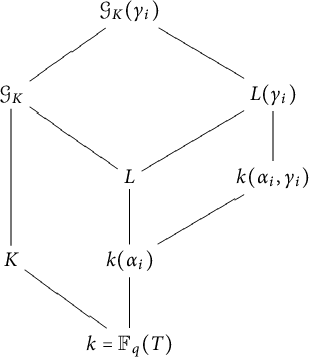
We now show that
$\mathcal {G}_{K}({\gamma }_i)$
is a subfield of
$H_{K}$
for
$1 \leq i \leq {\lambda }_2$
. We point out that
$\mathcal {G}_{K}({\gamma }_i)/\mathcal {G}_{K}$
is an abelian extension by the fact that it is the Artin–Schreier function field. It suffices to show that
$\mathcal {G}_{K}({\gamma }_i)/\mathcal {G}_{K}$
is an unramified extension and all the infinite places of
$\mathcal {G}_{K}$
split completely in
$\mathcal {G}_{K}({\gamma }_i)$
. By Lemma 4.1,
$k({\alpha }_i,{\gamma }_i)/k({\alpha }_i)$
is an unramified extension and all the infinite places of
$k({\alpha }_i)$
split completely in
$k({\alpha }_i,{\gamma }_i)$
. Thus,
$L({\gamma }_i)/L$
is an unramified extension; hence,
$\mathcal {G}_{K}({\gamma }_i)/\mathcal {G}_{K}$
is an unramified extension.
Now, we show that all the infinite places of
$\mathcal {G}_{K}$
split completely in
$\mathcal {G}_{K}({\gamma }_i)$
. Every infinite place of
$k({\alpha }_i)$
splits completely in
$k({\alpha }_i,{\gamma }_i)$
as shown above and all the infinite places of L split completely in
$L({\gamma }_i)$
. Also, all the infinite places split completely in
$L/k({\alpha }_i)$
by Lemma 2.1. Consequently, all the infinite places of L split completely in the compositum
$L({\gamma }_i)$
of L and
$k({\alpha }_i,{\gamma }_i)$
.
Let
$\mathcal {P}_\infty $
be a place of L which lies above the infinite place
$\infty $
of k and
$\mathcal {P}'$
a place of
$\mathcal {G}_{K}$
which lies above
$\mathcal {P}_\infty $
. We consider the following two possible cases:
$\mathcal {P}_\infty $
splits completely in
$\mathcal {G}_{K}$
or
$\mathcal {P}_\infty $
is totally ramified or inert in
$\mathcal {G}_{K}$
. We note that the result follows immediately in the former case; thus, it is sufficient to consider the latter case where there is exactly one place lying above
$\mathcal {P}_\infty $
in
$\mathcal {G}_{K}$
, the number of places in
$\mathcal {G}_{K}({\gamma }_i)$
which lie above
$\mathcal {P}'$
is exactly p; this is because the infinite places split completely in
$L({\gamma }_i)/L$
. Therefore,
$\mathcal {P}'$
splits completely in
$\mathcal {G}_{K}({\gamma }_i)$
, and the result holds.
We have
$\mathcal {H} = \mathcal {G}_{K}({\gamma }_1, \ldots , {\gamma }_{{\lambda }_2})$
since
$\mathcal {G}_{K}({\gamma }_i) \subseteq H_{K}$
and
$[\mathcal {H}:\mathcal {G}_{K}] = p^{{\lambda }_2}$
. We get
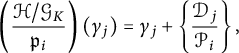$$ \begin{align*}\left( \frac{\mathcal{H}/\mathcal{G}_{K}}{{\mathfrak p}_i} \right)({\gamma}_j) = {\gamma}_j + \left\{ \frac{\mathcal{D}_j}{\mathcal{P}_i} \right\},\end{align*} $$
where
${\mathfrak p}_i$
is a place of
$\mathcal {G}_{K}$
lying above
$\mathcal {P}_i$
for
$1 \leq i \leq {\lambda }_2$
by the action of the Artin map in the Artin–Schreier function field. Therefore, we determine
$\mathcal {R}=[\mathfrak {r}_{ij}]= \left \{\frac {\mathcal {D}_j}{\mathcal {P}_i}\right \}$
.
This process is implemented in Algorithm 1. Steps (1) and (2) of Algorithm 1 give the process of computing
${\lambda }_1$
,
${\lambda }_2$
, and the Rédei matrix R. Step (3) explains the case where
${\lambda }_2=0$
and then the algorithm stops. If
$0<{\lambda }_2 <{\lambda }_1$
, then we go to Step (4.1), and if
${\lambda }_2 = {\lambda }_1$
, then we proceed with Step (4.2). Steps (5.1) and (5.2) explain the process of finding
$\mathcal {D}_i$
for
$1 \leq i \leq {\lambda }_2$
. In Step (6), we determine a matrix
$\mathcal {R}$
over
${\mathbb F}_p$
, and finally we obtain
${\lambda }_3 = {\lambda }_2 - \mbox {rank}(\mathcal {R})$
in Step (7).
Corollary 4.4 Let K be the Artin–Schreier quadratic extension over k, and let the
${\lambda }_3$
-rank of
$Cl_K$
be computed by Algorithm 1. Then the
$2^3$
-rank of
$Cl_K$
is exactly
${\lambda }_3$
: that is,
$Cl_K(2)$
has a subgroup isomorphic to
$({\mathbb Z}/2^3{\mathbb Z})^{{\lambda }_3}$
.
Proof This follows immediately from the fact that
${\lambda }_n$
is exactly equal to the full
$2^n$
-rank of
$Cl_K$
and Theorem 4.3.
Remark 4.5 For readers, focusing on the case:
$p=2$
, we first briefly explain the analogy between Rédei symbols (the 4-rank of the class groups) and the 8-rank of the class groups in the quadratic field case (for more details, see [Reference Iadarola9]). Then we describe the analogy between Artin–Schreier quadratic extensions over k and quadratic extensions over
${\mathbb Q}$
for computation of
${\lambda }_3$
.
Let F be a quadratic extension over
${\mathbb Q}$
, and let
$Cl_F$
be the ideal class group of F. Let
$r_4$
(resp.
$r_8$
) be the
$2^2$
-rank (resp.
$2^3$
-rank) of
$Cl_F$
. Let H be the Hilbert class field of F, and let
$H_n$
be the unramified abelian subextension of H such that
$\operatorname {\mathrm {Gal}}(H_n/F) \simeq Cl_F/Cl_F^n$
for
$n=2,4$
.
Basically, a strategy for computing the
$2^2$
-rank (resp.
$2^3$
-rank) is explicitly finding a subextension
$H_2$
(resp.
$H_4$
) of the Hilbert class field of F whose Galois group is isomorphic to
$\operatorname {\mathrm {Gal}}(Cl_F/Cl_F^2)$
(resp.
$\operatorname {\mathrm {Gal}}(Cl_F^2/Cl_F^4)$
).
Define two maps as follows:
$$ \begin{align*} &R_4 : {\mathbb F}_2^t \rightarrow Cl_F[2] \xrightarrow{\varphi} Cl_F/Cl_F^2 \xrightarrow{\simeq} \operatorname{\mathrm{Gal}}(H_2/F) \rightarrow \operatorname{\mathrm{Gal}}(H_2/{\mathbb Q}) = \prod_{i=1}^t \operatorname{\mathrm{Gal}}({\mathbb Q}(\sqrt{d_i})/{\mathbb Q}),\\ &R_8 : \operatorname{\mathrm{Ker}} R_4 \rightarrow Cl_F[2] \cap Cl_F^2 \xrightarrow{\psi} Cl_F^2/Cl_F^4 \xrightarrow{\simeq} \operatorname{\mathrm{Gal}}(H_4/H_2) = \prod_{i=1}^{r_4}\operatorname{\mathrm{Gal}}(H_2(\sqrt{{\alpha}_i})/H_2) \rightarrow {\mathbb F}_2^{r_4}, \end{align*} $$
where t is the number of finite primes of
${\mathbb Q}$
which are ramified in F,
$Cl_F[2]$
is the 2-torsion part of
$Cl_F$
, and the maps
$\varphi $
and
$\psi $
are induced by the inclusion maps. For computation of
$r_4$
and
$r_8$
, we find appropriate
$d_i$
(
$1 \leq i \leq t$
) and
${\alpha }_i$
(
$1\leq i \leq r_4)$
. Then we have
$$ \begin{align*}r_4 = t-\dim_{{\mathbb F}_2}R_4 \quad \text{and} \quad r_8=r_4-\dim_{{\mathbb F}_2}R_8.\end{align*} $$
To show the analogy between Artin–Schreier quadratic extensions over k and quadratic extensions over
${\mathbb Q}$
for computation of
${\lambda }_3$
(
$2^3$
-rank), let K be the Artin–Schreier quadratic extension over k. Then the map
$R_8$
corresponds to the map
$\Psi $
defined in (4.10):
$$ \begin{align*} \Psi: Cl_{K}(2)^G \cap Cl_{K}^{2} \rightarrow Cl_{K}^{2}/Cl_{K}^{4} \xrightarrow{\simeq} \mathrm{Gal}(\mathcal{H}/\mathcal{G}_{K}). \end{align*} $$
Then we have
${\lambda }_3 = {\lambda }_2 - \operatorname {\mathrm {rank}}\mathcal {R}$
, where
$\mathcal {R}$
is a matrix over
${\mathbb F}_2$
representing the map
$\Psi $
. We recall that
${\lambda }_3$
is the
$2^3$
-rank of
$Cl_K$
.
5 An infinite family of Artin–Schreier function fields with higher
${\lambda }_n$
-rank
In this section, we find an infinite family of Artin–Schreier function fields which have prescribed
${\lambda }_n$
-rank of the ideal class group for
$1 \leq n \leq 3$
. In Theorem 5.1, for any positive integer
$t \ge 2$
, we obtain an infinite family of Artin–Schreier extensions over k whose
${\lambda }_1$
-rank is t,
${\lambda }_2$
-rank is
$t-1$
, and
${\lambda }_3$
-rank is
$t-2$
. Then Corollary 5.3 shows the case where
$p=2$
, for a given positive integer
$t \ge 2$
, we obtain an infinite family of the Artin–Schreier quadratic extensions over k whose
$2$
-class group rank (resp.
$2^2$
-class group rank and
$2^3$
-class group rank) is exactly t (resp.
$t-1$
and
$t-2$
). Furthermore, we also obtain a similar result on the
$2^n$
-ranks of the divisor class groups of the Artin–Schreier quadratic extensions over k in Corollary 5.4.
Throughout this section, we define
$D_m$
as follows.
Notation 1 Let
$D_m := \sum _{i=1}^m D_i +f(T)$
be defined in (2.1) with
$D_i = Q_i/P_i^{r_i}$
, where
$m, P_i, Q_i$
, and
$f(T)$
satisfy one of the followings:
-
(i)
$m = \left \{ \begin {array}{ll} t, & \text {if}\ \deg f(T) \geq 1\\[3pt] & \text { or}\ f(T) = c \in {\mathbb F}_q^\times \ \text {such that}\ x^p-x=c\ \text {is irreducible over}\ {\mathbb F}_q,\\[5pt] t+1, & \text {if}\ f(T) = 0. \end {array} \right.$
-
(ii)
$Q_j \equiv P_j^{r_j}(b_i(T)^q-b_i(T))\ \pmod {P_i}$
for any
$1 \leq i \ne j \leq m$
except
$(i,j) = (1,2)$
, where
$b_i(T) \in {\mathbb F}_q[T]$
. -
(iii) If
$\deg f(T) \geq 1$
, then
$f(T) \equiv P_j^{r_j}(b_i(T)^q-b_i(T))\ \pmod {P_i}$
, where
$b_i(T) \in {\mathbb F}_q[T]$
for any
$1 \leq i \leq m$
. -
(iv) If
$f(T) \in {\mathbb F}_q^\times $
, then
$q \mid \deg P_i$
for any i with
$1 \leq i \leq m$
. -
(v)
$Q_j^{-1} \equiv P_j^{r_j}(b_i(T)^q-b_i(T))\ \pmod {P_i}$
, where
$b_i(T) \in {\mathbb F}_q[T]$
and
$Q_j^{-1}$
denotes the inverse of
$Q_j$
modulo
$P_i$
for any
$1 \leq i \ne j \leq m$
except
$(i,j) \ne (1,2)$
.
Theorem 5.1 For a given positive integer
$t \ge 2$
, there is an infinite family of Artin–Schreier extensions over k whose
${\lambda }_1$
-rank is t,
${\lambda }_2$
-rank is
$t-1$
, and
${\lambda }_3$
-rank is
$t-2$
.
Let
be the Artin–Schreier function field over k of extension degree p, where
$D_m$
is defined in Notation 1 and
is a root of
$x^p-x = D_m$
. Then the ideal class group
$Cl_K$
of K has
${\lambda }_1 = t$
,
${\lambda }_2 = t-1$
, and
${\lambda }_3 = t-2$
.
Remark 5.2 Let
${\mathbb F}_q$
be a finite field of order q, t be a given integer, and
$f(T) \in {\mathbb F}_q$
. By condition (i),
$m = t+1$
. By condition (ii), we can choose monic irreducible polynomials
$P_i \in {\mathbb F}_q[T]$
whose degrees are divisible by p. We note that conditions (iii) and (iv) can be interpreted as
$$ \begin{align} \left\{ \frac{D_j}{P_i} \right\} = \left\{ \frac{Q_j^{-1}}{P_i} \right\}=0; \end{align} $$
by the surjectivity of the trace map, there always exist
$D_j$
and
$Q_j^{-1}$
which satisfy (5.1). Since our choice of
$P_i$
’s are infinite, we have an infinite family of Artin–Schreier extensions which satisfy the conditions in Theorem 5.1.
Proof of Theorem 5.1
Recall that
${\lambda }_2 = {\lambda }_1 - \operatorname {\mathrm {rank}}(R)$
and
${\lambda }_3 = {\lambda }_2 - \operatorname {\mathrm {rank}}(\mathcal {R})$
, where R (resp.
$\mathcal {R}$
) is a matrix over
${\mathbb F}_p$
defined in Lemma 2.2 (resp. Algorithm 1). We need to show that
$$ \begin{align} {\lambda}_1 = t, \qquad {\lambda}_2 = t-1, \qquad {\lambda}_3 = t-2; \end{align} $$
this is equivalent to
$\operatorname {\mathrm {rank}}(R)= \operatorname {\mathrm {rank}}(\mathcal {R}) = 1$
.
We divide into the following three cases:
$\deg f(T) \geq 1$
,
$\deg f(T) = 0$
, and
$f(T) = c$
, where
$x^p-x-c$
is irreducible over
${\mathbb F}_q$
.
Case I.
$\deg f(T) \geq 1$
: that is, the infinite place of k is totally ramified in K.
Since
$\deg f(T) \geq 1$
, we have
$m=t$
by condition (i); this implies that
${\lambda }_1 = m = t$
by Lemma 2.2. For computing
${\lambda }_2$
, we compute every entry of the Rédei matrix R: that is, the Hasse norm
$\{D_j/P_i\}$
and
$\{f(T)/P_i\}$
for
$1 \leq i \ne j \leq m$
. Using Lemma 3.1 and condition (ii), we can easily obtain that
$\left \{ \frac {D_2}{P_1} \right \} \ne 0$
and
$\left \{ \frac {D_j}{P_i} \right \} = 0$
for any
$1 \leq i \ne j\leq m$
except
$(i, j) \ne (1,2)$
. Furthermore, we get
$\left \{ \frac {f}{P_i} \right \} = 0$
for any
$1 \leq i \leq m$
by condition (iii). Therefore, the Rédei matrix R can be written as
${\small {R = \left [ \begin {array}{cccc} p-1 & 1 & \cdots & 0\\ 0 & 0 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0& \cdots & 0 \\ \end {array} \right ]}};$
thus,
${\lambda }_2 = {\lambda }_1 - \operatorname {\mathrm {rank}}(R) = t-1$
. Lastly, we compute
${\lambda }_3$
of K using Algorithm 1 and Theorem 4.3. Using the definition of a matrix
$\mathcal {R}$
which is given in Algorithm 1, it suffices to compute
$\left \{\frac {1/Q_j}{P_i} \right \}$
for
$1 \leq i \ne j \leq m$
. By the same reasoning as in the computation of R, we get
${\lambda }_3 = {\lambda }_2 - \operatorname {\mathrm {rank}}(\mathcal {R}) = t-2$
. Therefore, (5.2) follows.
Case II.
$\deg f(T) = 0$
: that is, the infinite place of k splits completely in K, which is a real extension.
We can easily obtain
${\lambda }_1=t$
by using Lemma 2.2 and the condition
$m=t+1$
. For computing
${\lambda }_2$
, we compute every entry of the Rédei matrix R: that is, the value of Hasse norm
$\{D_j/P_i\}$
for
$1 \leq i \ne j \leq m$
. By the definition of Hasse norm which is defined in Definition 2.1, we get
$\{D_2/P_1\} \ne 0$
and
$\{D_j/P_i\} = 0$
, where
$1 \leq i \ne j \leq m$
except
$(i,j) = (1,2)$
. As in Case 1, the rank of Rédei matrix is one: that is,
${\lambda }_2 = {\lambda }_1 - \operatorname {\mathrm {rank}}(R) = t-1$
. Lastly, we compute
${\lambda }_3$
of K; by the same computation method as in Case I, we have
${\lambda }_3 = {\lambda }_2 - \operatorname {\mathrm {rank}}(\mathcal {R}) = t-2$
. Therefore, (5.2) follows.
Case III.
$f(T) = c \in {\mathbb F}_q^\times $
, where
$x^p-x-c$
is irreducible over
${\mathbb F}_q$
: that is, the infinite place of k is inert in K.
Under this assumption, K is an imaginary extension; so,
$m = t$
. We claim that (5.2) holds for this case. We can simply get
${\lambda }_1 = t$
by Lemma 2.2 and we also obtain
$\left \{ D_j/ P_i \right \} = 0$
for every
$1 \leq i \ne j \leq t = m$
except
$(i,j) = (1,2)$
by using the same reasoning as in Case I. Now, we compute the value of
$\left \{ c/P_i\right \}$
for
$1 \leq i \leq t=m$
, where
$c \in {\mathbb F}_q^\times $
. We have
$$ \begin{align*} \left\{ \frac{c}{P_i} \right\} = \operatorname{\mathrm{Tr}}_{{\mathbb F}_{q}/{\mathbb F}_p} (\operatorname{\mathrm{Tr}}_{{\mathbb F}_{\mathfrak{d}}/{\mathbb F}_q} c) = \operatorname{\mathrm{Tr}}_{{\mathbb F}_q/{\mathbb F}_p} (c \deg {P_i}) = \deg {P_i} (\operatorname{\mathrm{Tr}}_{{\mathbb F}_q/{\mathbb F}_p} c); \end{align*} $$
the second equation holds since c is a nonzero element of
${\mathbb F}_q$
and the last equation holds by the property of a trace map over a finite field. We get
$\deg {P_i}(\operatorname {\mathrm {Tr}}_{{\mathbb F}_q/{\mathbb F}_p} c) = 0$
in
${\mathbb F}_p$
by Lemma 3.1 by the assumption that
$q \mid \deg {P_i}$
for every
$1 \leq i \leq m$
; therefore, (3.5) is zero in
${\mathbb F}_p$
. Hence,
${\lambda }_2 = t-1$
. By the same reasoning as in Case I,
${\lambda }_3 = t-2$
and we have (5.2).
Corollary 5.3 Let
be the Artin–Schreier quadratic function field over k of extension degree
$2$
, where
$D_m$
is defined in Notation
$1$
and
is a root of
$x^2-x = D_m$
.
For any positive integer
$t \ge 2$
, there is an infinite family of Artin–Schreier quadratic extensions over k whose
$2$
-class group rank is exactly t,
$2^2$
-class group rank is
$t-1$
, and
$2^3$
-class group rank is
$t-2$
.
In particular,
$Cl_K(2)$
contains a subgroup isomorphic to
$({\mathbb Z}/2^n{\mathbb Z})^{t-n+1}$
for
$1 \leq n \leq 3$
.
Proof We note that
${\lambda }_n$
is exactly equal to the full
$2^n$
-rank (
$1 \leq n \leq 3$
) of the ideal class group
$Cl_K$
of K; therefore, the result follows immediately from Theorem 5.1.
Corollary 5.4 For a given positive integer t, let
be the Artin–Schreier quadratic function field over k, where
$D_m = \sum _{i=1}^m Q_i/P_i^{r_i} + f(T)$
such that
$P_i, Q_i, f(T)$
, and m satisfy the conditions (i)–(v) in Notation 1. Let
$J_K$
be the divisor class group of K. Then we have the following infinite family of Artin–Schreier quadratic extensions.
-
(i) For
$t \ge 2$
, if
$\deg f(T) \ge 1$
(equivalently,
$\infty $
is totally ramified in K), then the
$2^n$
-class group rank of
$J_K$
is exactly equal to
$t+1-n$
for
$1 \leq n \leq 3$
. -
(ii) For
$t \ge 2$
, if
$f(T) =0$
(equivalently,
$\infty $
splits completely in K), then the
$2^n$
-class group rank of
$J_K$
is exactly either
$t+1-n$
or
$t+2-n$
for
$1 \leq n \leq 3$
. -
(iii) For
$t \ge 3$
, if
$f(T) \in {\mathbb F}_q^\times $
(equivalently,
$\infty $
is inert in K), then the
$2^n$
-class group rank of
$J_K$
is exactly either
$t+1-n$
or
$t-n$
for
$1 \leq n \leq 3$
.
Proof Since
$D_m$
satisfies the conditions (i)–(v) in Notation 1, the ideal class group
$Cl_K$
of K has
${\lambda }_1$
-rank t,
${\lambda }_2$
-rank
$t-1$
, and
${\lambda }_3$
-rank
$t-2$
.
We first assume that
$\deg f(T) \geq 1$
: that is, the infinite place
$\infty $
of k is totally ramified in K. Then the ideal class group
$Cl_K$
of K is isomorphic to the divisor class group
$J_K$
of K by Lemma 2.6. Thus, by Lemma 5.3, the
$2^n$
-rank of the divisor class group
$J_K$
of K is
$t+1-n$
for n up to 3; thus, (i) follows.
Next, suppose that
$f(T) = 0$
. This is the case where the infinite place
$\infty $
of k splits completely in K. Then, by Lemma 2.6, we note that
$J_K/R$
is isomorphic to
$Cl_K$
, where R denotes the group
$\mathcal {D}_K^0(S)/\mathcal {P}_K(S)$
. By the fact the group R is a cyclic group, the
$2^n$
-rank of the divisor class group
$J_K$
is either
$t+1-n$
or
$t+2-n$
for n up to 3.
Finally, we assume that
$f(T) \in {\mathbb F}_q^\times $
: the case where
$\infty $
is inert in K. Then, by the exact sequence given in Lemma 2.6(ii), we get
$|Cl_K| = 2|J_K|$
. Since
$Cl_K(2)$
contains a subgroup isomorphic to
$({\mathbb Z}/2^n{\mathbb Z})^{t-n+1}$
for
$1 \le n \le 3$
,
$J_K(2)$
contains a subgroup isomorphic to
$({\mathbb Z}/2^n{\mathbb Z})^{t-n+1}$
or
$({\mathbb Z}/2^n{\mathbb Z})^{t-n}$
for
$1 \leq n \le 3$
; therefore, (iii) holds.
Remark 5.5 We briefly mention that the
${\lambda }_2$
-rank is connected to the embedding problem. For instance, in the quadratic number field
$F = {\mathbb Q}(\sqrt {d})$
, the solvability of the conics
$X^2 = aY^2 + \frac {d}{a}Z^2$
yields unramified cyclic quartic extensions of F. The solvability of this conic is related to the
$\lambda _2$
-rank of
$Cl_F$
, which is computed by the Rédei matrix in terms of Legendre symbols. Then the embedding problem for F is not solvable. On the other hand, in our context, the embedding problem for Artin–Schreier extensions K over k is solvable and every finite place of k is wildly ramified in K.
Table 1: Infinite families of Artin–Schreier extensions
$K=k({\alpha }_D)$
over k whose
${\lambda }_1$
-rank of the ideal class groups is t and
${\lambda }_n$
-rank is zero for
$n\ge 2$
, where
${\alpha }_D^p-{\alpha }_D = D$
.
Table 2: Infinite families of Artin–Schreier extensions
$K=k({\alpha }_D)$
over k whose
${\lambda }_1$
-rank of the ideal class groups is t,
${\lambda }_2$
-rank is
$t-1$
, and
${\lambda }_3$
-rank is
$t-2$
, where
${\alpha }_D^p-{\alpha }_D = D$
.
6 Implementation results
In this section, as implementation results, we explicitly present concrete infinite families of Artin–Schreier extensions over k whose ideal class groups have guaranteed prescribed
${\lambda }_n$
-rank of the ideal class group for
$1 \leq n \leq 3$
. In Table 1, for a given positive integer t, we obtain explicit families of Artin–Schreier extensions K over k whose
${\lambda }_1$
-rank of the ideal class group
$Cl_K$
is t and
${\lambda }_n$
-rank is zero for
$n \ge 2$
, depending on the ramification behavior of the infinite place
$\infty $
of k (Theorems 3.2–3.4). Furthermore, in Table 2, for a given integer
$t \ge 2$
, we get explicit families of Artin–Schreier extensions over k whose
${\lambda }_1$
-rank of the ideal class groups is t,
${\lambda }_2$
-rank is
$t-1$
, and
${\lambda }_3$
-rank is
$t-2$
(Theorem 5.1). In the tables, we denote
${\mathbb Z}/m{\mathbb Z}$
by
${\mathbb Z}_m$
for a positive integer m.
Acknowledgment
The authors would like to thank the reviewer for his/her valuable comments for improving the clarity of this paper; in particular, we added Remark 5.5 based on the reviewer’s comments. Some partial results of this paper (Section 4) were obtained in the Ph.D. thesis [Reference Yoo21] of the first author under the supervision of Prof. Yoonjin Lee.
Open access
