No CrossRef data available.
Article contents
Integral Formula for Spectral Flow for 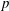 $p$-Summable Operators
$p$-Summable Operators
Published online by Cambridge University Press: 07 January 2019
Abstract
Fix a von Neumann algebra 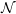 ${\mathcal{N}}$ equipped with a suitable trace
${\mathcal{N}}$ equipped with a suitable trace  $\unicode[STIX]{x1D70F}$. For a path of self-adjoint Breuer–Fredholm operators, the spectral flow measures the net amount of spectrum that moves from negative to non-negative. We consider specifically the case of paths of bounded perturbations of a fixed unbounded self-adjoint Breuer–Fredholm operator affiliated with
$\unicode[STIX]{x1D70F}$. For a path of self-adjoint Breuer–Fredholm operators, the spectral flow measures the net amount of spectrum that moves from negative to non-negative. We consider specifically the case of paths of bounded perturbations of a fixed unbounded self-adjoint Breuer–Fredholm operator affiliated with 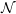 ${\mathcal{N}}$. If the unbounded operator is
${\mathcal{N}}$. If the unbounded operator is 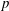 $p$-summable (that is, its resolvents are contained in the ideal
$p$-summable (that is, its resolvents are contained in the ideal 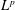 $L^{p}$), then it is possible to obtain an integral formula that calculates spectral flow. This integral formula was first proved by Carey and Phillips, building on earlier approaches of Phillips. Their proof was based on first obtaining a formula for the larger class of
$L^{p}$), then it is possible to obtain an integral formula that calculates spectral flow. This integral formula was first proved by Carey and Phillips, building on earlier approaches of Phillips. Their proof was based on first obtaining a formula for the larger class of 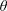 $\unicode[STIX]{x1D703}$-summable operators, and then using Laplace transforms to obtain a
$\unicode[STIX]{x1D703}$-summable operators, and then using Laplace transforms to obtain a 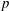 $p$-summable formula. In this paper, we present a direct proof of the
$p$-summable formula. In this paper, we present a direct proof of the 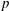 $p$-summable formula that is both shorter and simpler than theirs.
$p$-summable formula that is both shorter and simpler than theirs.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018

