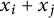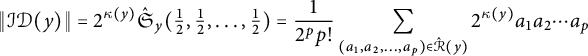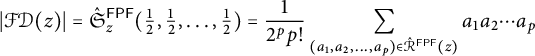1 Introduction
One can identify the equivariant cohomology rings for the spaces of symmetric and skew-symmetric complex matrices with multivariate polynomial rings. Under this identification, we show that the classes of certain natural subvarieties of (skew-)symmetric matrices are given by the involution Schubert polynomials introduced by Wyser and Yong in [Reference Wyser and Yong45]. These classes of varieties generalize various others studied in the settings of degeneracy loci and combinatorial commutative algebra, for instance the (skew-)symmetric determinantal varieties studied by Harris and Tu [Reference Harris and Tu16].
Involution Schubert polynomials have a combinatorial formula for their monomial expansion [Reference Hamaker, Marberg and Pawlowski13]. As a consequence of our geometric results, they must also expand as sums of products of binomials
![]() $x_i + x_j$
. We give a combinatorial description of these expansions, which is a new analogue of the classic Billey–Jockusch–Stanley expansion for ordinary Schubert polynomials [Reference Billey, Jockusch and Stanley3]. This description is far more compact than the monomial expansion. Our formulas involve novel objects that we call involution pipe dreams. Involution pipe dreams appear to be the fundamental objects necessary to replicate Knutson and Miller’s program [Reference Knutson and Miller23] to understand our varieties from a commutative algebra perspective.
$x_i + x_j$
. We give a combinatorial description of these expansions, which is a new analogue of the classic Billey–Jockusch–Stanley expansion for ordinary Schubert polynomials [Reference Billey, Jockusch and Stanley3]. This description is far more compact than the monomial expansion. Our formulas involve novel objects that we call involution pipe dreams. Involution pipe dreams appear to be the fundamental objects necessary to replicate Knutson and Miller’s program [Reference Knutson and Miller23] to understand our varieties from a commutative algebra perspective.
1.1 Three flavors of matrix Schubert varieties
Fix a positive integer n. Let
![]() $\mathsf {GL}_n$
denote the general linear group of complex
$\mathsf {GL}_n$
denote the general linear group of complex
![]() $n\times n$
invertible matrices, and write
$n\times n$
invertible matrices, and write
![]() $\mathsf {B}$
and
$\mathsf {B}$
and
![]() $\mathsf {B}^+$
for the Borel subgroups of lower- and upper-triangular matrices in
$\mathsf {B}^+$
for the Borel subgroups of lower- and upper-triangular matrices in
![]() $\mathsf {GL}_n$
. Our work aims to extend what is known about the geometry of the
$\mathsf {GL}_n$
. Our work aims to extend what is known about the geometry of the
![]() $\mathsf {B}$
-orbits on matrix space to symmetric and skew-symmetric matrix spaces.
$\mathsf {B}$
-orbits on matrix space to symmetric and skew-symmetric matrix spaces.
We begin with some classical background. Consider the type A flag variety
![]() $\textsf {Fl}_{n} = \mathsf {B} \backslash \mathsf {GL}_n$
. The subgroup
$\textsf {Fl}_{n} = \mathsf {B} \backslash \mathsf {GL}_n$
. The subgroup
![]() $\mathsf {B}^+$
acts on
$\mathsf {B}^+$
acts on
![]() $\textsf {Fl}_{n} $
with finitely many orbits, which are naturally indexed by permutations w in the symmetric group
$\textsf {Fl}_{n} $
with finitely many orbits, which are naturally indexed by permutations w in the symmetric group
![]() $S_n$
of permutations of
$S_n$
of permutations of
![]() $\{1,2,\dots ,n\}$
. These orbits afford a CW decomposition of
$\{1,2,\dots ,n\}$
. These orbits afford a CW decomposition of
![]() $\textsf {Fl}_{n}$
, so the cohomology classes of their closures
$\textsf {Fl}_{n}$
, so the cohomology classes of their closures
![]() $X_w$
, the Schubert varieties, form a basis for the integral singular cohomology ring
$X_w$
, the Schubert varieties, form a basis for the integral singular cohomology ring
![]() $H^*(\textsf {Fl}_{n})$
. Borel’s isomorphism explicitly identifies
$H^*(\textsf {Fl}_{n})$
. Borel’s isomorphism explicitly identifies
![]() $H^*(\textsf {Fl}_{n})$
with a quotient of the polynomial ring
$H^*(\textsf {Fl}_{n})$
with a quotient of the polynomial ring
![]() $\mathbb {Z}[x_1,\dots ,x_n]$
, and the Schubert polynomials
$\mathbb {Z}[x_1,\dots ,x_n]$
, and the Schubert polynomials
![]() $\mathfrak {S}_w \in \mathbb {Z}[x_1,\dots ,x_n]$
are (nonunique) representatives for the Schubert classes
$\mathfrak {S}_w \in \mathbb {Z}[x_1,\dots ,x_n]$
are (nonunique) representatives for the Schubert classes
![]() $[X_w] \in H^*(\textsf {Fl}_{n})$
.
$[X_w] \in H^*(\textsf {Fl}_{n})$
.
The maximal torus
![]() $\mathsf {T}$
of diagonal matrices in
$\mathsf {T}$
of diagonal matrices in
![]() $\mathsf {GL}_n$
also acts on
$\mathsf {GL}_n$
also acts on
![]() $\textsf {Fl}_{n}$
, so we can instead consider the equivariant cohomology ring
$\textsf {Fl}_{n}$
, so we can instead consider the equivariant cohomology ring
![]() $H^*_{\mathsf {T}}(\textsf {Fl}_{n})$
. Via an extension of Borel’s isomorphism, this ring is isomorphic to a quotient of
$H^*_{\mathsf {T}}(\textsf {Fl}_{n})$
. Via an extension of Borel’s isomorphism, this ring is isomorphic to a quotient of
![]() $\mathbb {Z}[x_1, \ldots , x_n, y_1, \ldots , y_n]$
. Lascoux and Schützenberger [Reference Lascoux and Schützenberger27] introduced the double Schubert polynomials
$\mathbb {Z}[x_1, \ldots , x_n, y_1, \ldots , y_n]$
. Lascoux and Schützenberger [Reference Lascoux and Schützenberger27] introduced the double Schubert polynomials
![]() $\mathfrak {S}_w(x,y)$
to represent the equivariant classes
$\mathfrak {S}_w(x,y)$
to represent the equivariant classes
![]() $[X_w]_{\mathsf {T}}\in H^*_{\mathsf {T}}(\textsf {Fl}_{n})$
. These representatives are distinguished in the following sense.
$[X_w]_{\mathsf {T}}\in H^*_{\mathsf {T}}(\textsf {Fl}_{n})$
. These representatives are distinguished in the following sense.
Let
![]() $\textsf {Mat}_n$
be the set of
$\textsf {Mat}_n$
be the set of
![]() $n\times n$
complex matrices and write
$n\times n$
complex matrices and write
![]() $\iota :\mathsf {GL}_n \hookrightarrow \textsf {Mat}_n$
for the obvious inclusion. The product group
$\iota :\mathsf {GL}_n \hookrightarrow \textsf {Mat}_n$
for the obvious inclusion. The product group
![]() $ \mathsf {T} \times \mathsf {T}$
acts on
$ \mathsf {T} \times \mathsf {T}$
acts on
![]() $A\in \textsf {Mat}_n$
by
$A\in \textsf {Mat}_n$
by
![]() $(t_1, t_2) \cdot A = t_1 A t_2^{-1}$
. The matrix Schubert variety of a permutation
$(t_1, t_2) \cdot A = t_1 A t_2^{-1}$
. The matrix Schubert variety of a permutation
![]() $w \in S_n$
is
$w \in S_n$
is
![]() $MX_w = \overline {\iota (X_w)}$
. Since
$MX_w = \overline {\iota (X_w)}$
. Since
![]() $M_n$
is
$M_n$
is
![]() $\mathsf {T} \times \mathsf {T}$
-equivariantly contractible,
$\mathsf {T} \times \mathsf {T}$
-equivariantly contractible,
![]() $H^*_{\mathsf {T} \times \mathsf {T}}(\textsf {Mat}_n) \cong H^*_{\mathsf {T} \times \mathsf {T}}(\text {point}) \cong \mathbb {Z}[x_1,\dots ,x_n,y_1,\dots ,y_n]$
. The launching point for Knutson and Miller’s program is the following theorem:
$H^*_{\mathsf {T} \times \mathsf {T}}(\textsf {Mat}_n) \cong H^*_{\mathsf {T} \times \mathsf {T}}(\text {point}) \cong \mathbb {Z}[x_1,\dots ,x_n,y_1,\dots ,y_n]$
. The launching point for Knutson and Miller’s program is the following theorem:
Theorem 1.1 [Reference Knutson and Miller23]
For all
![]() $w \in S_n$
, we have
$w \in S_n$
, we have
![]() $\mathfrak {S}_w(x,y) = [MX_w] \in H^*_{\mathsf {T} \times \mathsf {T}}(\textsf {Mat}_n)$
.
$\mathfrak {S}_w(x,y) = [MX_w] \in H^*_{\mathsf {T} \times \mathsf {T}}(\textsf {Mat}_n)$
.
As mentioned in the historical notes at the end of [Reference Miller and Sturmfels36, Chapter 15], Theorem 1.1 is equivalent to Fulton’s characterization of each
![]() $\mathfrak {S}_w(x,y)$
as the class of a certain degeneracy locus for vector bundle morphisms [Reference Fulton11].
$\mathfrak {S}_w(x,y)$
as the class of a certain degeneracy locus for vector bundle morphisms [Reference Fulton11].
Our results are related to the geometry of certain spherical varieties studied by Richardson and Springer in [Reference Richardson and Springer40]. Specifically, define the orthogonal group
![]() $\mathsf {O}_n$
as the subgroup of
$\mathsf {O}_n$
as the subgroup of
![]() $\mathsf {GL}_n$
preserving a fixed nondegenerate symmetric bilinear form on
$\mathsf {GL}_n$
preserving a fixed nondegenerate symmetric bilinear form on
![]() $\mathbb {C}^n$
, and when n is even define the symplectic group
$\mathbb {C}^n$
, and when n is even define the symplectic group
![]() $\mathsf {Sp}_n$
as the subgroup of
$\mathsf {Sp}_n$
as the subgroup of
![]() $\mathsf {GL}_n$
preserving a fixed nondegenerate skew-symmetric bilinear form.
$\mathsf {GL}_n$
preserving a fixed nondegenerate skew-symmetric bilinear form.
We consider the actions of
![]() $\mathsf {O}_n$
and
$\mathsf {O}_n$
and
![]() $\mathsf {Sp}_n$
(when n is even) on
$\mathsf {Sp}_n$
(when n is even) on
![]() $\mathsf {Fl}_{n}$
. The associated orbit closures
$\mathsf {Fl}_{n}$
. The associated orbit closures
![]() $\hat X_y$
and
$\hat X_y$
and
![]() $\hat X^{\mathsf {{FPF}}}_z$
are indexed by arbitrary involutions y and fixed-point-free involutions z in
$\hat X^{\mathsf {{FPF}}}_z$
are indexed by arbitrary involutions y and fixed-point-free involutions z in
![]() $S_n$
. Let
$S_n$
. Let
![]() $\kappa (y)$
denote the number of two-cycles in an involution
$\kappa (y)$
denote the number of two-cycles in an involution
![]() $y=y^{-1} \in S_n$
. Wyser and Yong [Reference Wyser and Yong45] constructed certain polynomials
$y=y^{-1} \in S_n$
. Wyser and Yong [Reference Wyser and Yong45] constructed certain polynomials
![]() $\hat {\mathfrak {S}}_y, \hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z \in \mathbb {Z}[x_1,\dots ,x_n]$
and showed that the classes
$\hat {\mathfrak {S}}_y, \hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z \in \mathbb {Z}[x_1,\dots ,x_n]$
and showed that the classes
![]() $[\hat X_y]$
and
$[\hat X_y]$
and
![]() $[\hat X^{\mathsf {{FPF}}}_z]$
are represented in
$[\hat X^{\mathsf {{FPF}}}_z]$
are represented in
![]() $H^*(\mathsf {Fl}_{n})$
by
$H^*(\mathsf {Fl}_{n})$
by
![]() $2^{\kappa (y)}\hat {\mathfrak {S}}_y$
and
$2^{\kappa (y)}\hat {\mathfrak {S}}_y$
and
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
. We refer to
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
. We refer to
![]() $\hat {\mathfrak {S}}_y$
and
$\hat {\mathfrak {S}}_y$
and
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
as involution Schubert polynomials; for their precise definitions, see Section 2.1.
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
as involution Schubert polynomials; for their precise definitions, see Section 2.1.
Write
![]() $\mathsf {SMat}_n$
and
$\mathsf {SMat}_n$
and
![]() $\mathsf {SSMat}_n$
for the sets of symmetric and skew-symmetric
$\mathsf {SSMat}_n$
for the sets of symmetric and skew-symmetric
![]() $n\times n$
complex matrices. Let
$n\times n$
complex matrices. Let
![]() $t \in \mathsf {T}$
act on these spaces by
$t \in \mathsf {T}$
act on these spaces by
![]() $t\cdot A = tAt$
. One can identify the
$t\cdot A = tAt$
. One can identify the
![]() $\mathsf {T}$
-equivariant cohomology rings of both spaces with
$\mathsf {T}$
-equivariant cohomology rings of both spaces with
![]() $\mathbb {Z}[x_1, \ldots , x_n]$
; see the discussion in Section 2.2. For each involution
$\mathbb {Z}[x_1, \ldots , x_n]$
; see the discussion in Section 2.2. For each involution
![]() $y \in S_n$
, let
$y \in S_n$
, let
![]() $M\hat X_y = MX_y \cap \mathsf {SMat}_n$
. Similarly, for each fixed-point-free involution
$M\hat X_y = MX_y \cap \mathsf {SMat}_n$
. Similarly, for each fixed-point-free involution
![]() $z \in S_n$
, let
$z \in S_n$
, let
![]() $M\hat X^{\mathsf {{FPF}}}_z = MX_z \cap \mathsf {SSMat}_n$
. Our first main result is a (skew-)symmetric analogue of Theorem 1.1:
$M\hat X^{\mathsf {{FPF}}}_z = MX_z \cap \mathsf {SSMat}_n$
. Our first main result is a (skew-)symmetric analogue of Theorem 1.1:
Theorem 1.2 For all involutions y and fixed-point-free involution z in
![]() $S_n$
, we have
$S_n$
, we have
![]() $ 2^{\kappa (y)}\hat {\mathfrak {S}}_y = [M\hat X_y] \in H_{\mathsf {T}}^*(\mathsf {SMat}_n) $
and
$ 2^{\kappa (y)}\hat {\mathfrak {S}}_y = [M\hat X_y] \in H_{\mathsf {T}}^*(\mathsf {SMat}_n) $
and
![]() $ \hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z = [M\hat X^{\mathsf {{FPF}}}_z] \in H_{\mathsf {T}}^*(\mathsf {SSMat}_n). $
Thus, involution Schubert polynomials are also equivariant cohomology representatives for symmetric and skew-symmetric matrix varieties.
$ \hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z = [M\hat X^{\mathsf {{FPF}}}_z] \in H_{\mathsf {T}}^*(\mathsf {SSMat}_n). $
Thus, involution Schubert polynomials are also equivariant cohomology representatives for symmetric and skew-symmetric matrix varieties.
Our proof of this theorem appears in Section 2.3. An extension of Theorem 1.2 to complex K-theory appears in [Reference Marberg and Pawlowski31]. Theorem 1.2 was first announced in a conference proceedings before the appearance of the preprint version of [Reference Marberg and Pawlowski31], which precedes the preprint version of this article. The proof of Theorem 1.2 is a special case of results of [Reference Marberg and Pawlowski31].
Remark Another family of varieties in
![]() $\mathsf {SMat}_n$
indexed by permutations in
$\mathsf {SMat}_n$
indexed by permutations in
![]() $S_n$
has been studied by Fink et al. [Reference Fink, Rajchgot and Sullivant6]. However, their varieties are cut out by northeast rank conditions, while
$S_n$
has been studied by Fink et al. [Reference Fink, Rajchgot and Sullivant6]. However, their varieties are cut out by northeast rank conditions, while
![]() $M\hat X_y$
and
$M\hat X_y$
and
![]() $M\hat X^{\mathsf {{FPF}}}_z$
are cut out by northwest rank conditions (see (2.3) and (2.4) in Section 2.3). The varieties in [Reference Fink, Rajchgot and Sullivant6] are closely related to type C Schubert calculus and generally do not coincide with our
$M\hat X^{\mathsf {{FPF}}}_z$
are cut out by northwest rank conditions (see (2.3) and (2.4) in Section 2.3). The varieties in [Reference Fink, Rajchgot and Sullivant6] are closely related to type C Schubert calculus and generally do not coincide with our
![]() $M\hat X_y$
varieties.
$M\hat X_y$
varieties.
1.2 Three flavors of pipe dreams
If Z is a closed subvariety of
![]() $\mathsf {SMat}_n$
or
$\mathsf {SMat}_n$
or
![]() $\mathsf {SSMat}_n$
, then its
$\mathsf {SSMat}_n$
, then its
![]() $\mathsf {T}$
-equivariant cohomology class is a positive integer combination of products of binomials
$\mathsf {T}$
-equivariant cohomology class is a positive integer combination of products of binomials
![]() $x_i + x_j$
(see Corollary 2.10). Our second main result gives a combinatorial description of such an expansion for
$x_i + x_j$
(see Corollary 2.10). Our second main result gives a combinatorial description of such an expansion for
![]() $\hat {\mathfrak {S}}_y$
and
$\hat {\mathfrak {S}}_y$
and
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
.
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
.
Let
![]() $[n] = \{1, 2, \ldots , n\}$
and
$[n] = \{1, 2, \ldots , n\}$
and
![]() . Consider a subset
. Consider a subset
![]() . One associates to D a wiring diagram by replacing the cells
. One associates to D a wiring diagram by replacing the cells
![]() by tiles of two types, given either by a crossing of two paths (drawn as a
by tiles of two types, given either by a crossing of two paths (drawn as a
![]() tile) if
tile) if
![]() $(i,j) \in D$
or by two paths bending away from each other (drawn as a
$(i,j) \in D$
or by two paths bending away from each other (drawn as a
![]() tile) if
tile) if
![]() $(i,j) \notin D$
. Connecting the endpoints of adjacent tiles yields a union of n continuously differentiable paths, which we refer to as “pipes.” For example:
$(i,j) \notin D$
. Connecting the endpoints of adjacent tiles yields a union of n continuously differentiable paths, which we refer to as “pipes.” For example:

Definition 1.3 A subset
![]() is a reduced pipe dream if no two pipes in the associated wiring diagram cross more than once.
is a reduced pipe dream if no two pipes in the associated wiring diagram cross more than once.
This condition holds in the example (1.1). Pipe dreams as described here were introduced by Bergeron and Billey [Reference Bergeron and Billey1], inspired by related diagrams of Fomin and Kirillov [Reference Fomin and Kirillov9]. Bergeron and Billey originally referred to pipe dreams as reduced-word compatible sequence graphs or rc-graphs for short.
A reduced pipe dream D determines a permutation
![]() $w \in S_n$
in the following way. Label the left endpoints of the pipes in D’s wiring diagram by
$w \in S_n$
in the following way. Label the left endpoints of the pipes in D’s wiring diagram by
![]() $1, 2, \ldots , n$
from top to bottom, and the top endpoints by
$1, 2, \ldots , n$
from top to bottom, and the top endpoints by
![]() $1, 2, \ldots , n$
from left to right. Then the associated permutation
$1, 2, \ldots , n$
from left to right. Then the associated permutation
![]() $w \in S_n$
is the element such that the pipe with left endpoint i has top endpoint
$w \in S_n$
is the element such that the pipe with left endpoint i has top endpoint
![]() $w(i)$
. For instance, the permutation of
$w(i)$
. For instance, the permutation of
![]() $D=\{(1,3),(2,1)\}$
is
$D=\{(1,3),(2,1)\}$
is
![]() $w = 1423 \in S_4$
. Let
$w = 1423 \in S_4$
. Let
![]() $\mathcal {PD}(w)$
denote the set of all reduced pipe dreams associated to
$\mathcal {PD}(w)$
denote the set of all reduced pipe dreams associated to
![]() $w \in S_n$
.
$w \in S_n$
.
Pipe dreams are of interest for their role in formulas for
![]() $\mathfrak {S}_w$
and
$\mathfrak {S}_w$
and
![]() $\mathfrak {S}_w(x,y)$
. Lascoux and Schützenberger’s original definition of these Schubert polynomials in [Reference Lascoux and Schützenberger28] is recursive in terms of divided difference operators. However, by results of Fomin and Stanley [Reference Fomin and Stanley10, Section 4] we also have
$\mathfrak {S}_w(x,y)$
. Lascoux and Schützenberger’s original definition of these Schubert polynomials in [Reference Lascoux and Schützenberger28] is recursive in terms of divided difference operators. However, by results of Fomin and Stanley [Reference Fomin and Stanley10, Section 4] we also have
The first identity is the Billey–Jockusch–Stanley formula for Schubert polynomials [Reference Billey, Jockusch and Stanley3].
There are analogues of this formula for the involution Schubert polynomials
![]() $\hat {\mathfrak {S}}_y$
and
$\hat {\mathfrak {S}}_y$
and
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
, which involve the following new classes of pipe dreams. A reduced pipe dream
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
, which involve the following new classes of pipe dreams. A reduced pipe dream
![]() is symmetric if
is symmetric if
![]() $(i,j) \in D$
implies
$(i,j) \in D$
implies
![]() $(j,i) \in D$
, and almost-symmetric if both of the following properties hold:
$(j,i) \in D$
, and almost-symmetric if both of the following properties hold:
-
• If
 $(i, j) \in D$
where
$(i, j) \in D$
where
 $i< j$
then
$i< j$
then
 $(j,i) \in D$
.
$(j,i) \in D$
. -
• If
 $(j, i) \in D$
where
$(j, i) \in D$
where
 $i< j$
but
$i< j$
but
 $(i, j) \notin D$
, then the pipes crossing at
$(i, j) \notin D$
, then the pipes crossing at
 $(j, i)$
in the wiring diagram of D are also the pipes that avoid each other at
$(j, i)$
in the wiring diagram of D are also the pipes that avoid each other at
 $(i, j)$
.
$(i, j)$
.
Equivalently, D is almost-symmetric if it is as symmetric as possible while respecting the condition that no two pipes cross twice, and any violation of symmetry forced by this condition takes the form of a crossing
![]() $(j,i)$
below the diagonal rather than at the transposed position
$(j,i)$
below the diagonal rather than at the transposed position
![]() $(i,j)$
.
$(i,j)$
.
Let
![]() $\mathcal {I}_n=\{ w \in S_n : w=w^{-1}\}$
and write
$\mathcal {I}_n=\{ w \in S_n : w=w^{-1}\}$
and write
![]() $\mathcal {I}^{\mathsf {{FPF}}}_n$
for the subset of fixed-point-free elements of
$\mathcal {I}^{\mathsf {{FPF}}}_n$
for the subset of fixed-point-free elements of
![]() $\mathcal {I}_n$
. Note that n must be even for
$\mathcal {I}_n$
. Note that n must be even for
![]() $\mathcal {I}^{\mathsf {{FPF}}}_n$
to be nonempty. Also let
$\mathcal {I}^{\mathsf {{FPF}}}_n$
to be nonempty. Also let
Definition 1.4 The set of involution pipe dreams for
![]() $y \in \mathcal {I}_n$
is
$y \in \mathcal {I}_n$
is
The set of fpf-involution pipe dreams for
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_{n}$
is
$z \in \mathcal {I}^{\mathsf {{FPF}}}_{n}$
is
By convention, (fpf-)involution pipe dreams are always instances of reduced pipe dreams. It would be more precise to call our objects “reduced involution pipe dreams,” but since we will never consider any pipe dreams that are unreduced, we opt for more concise terminology.
We now state our second main result, which will reappear as Theorems 4.25 and 4.36.
Theorem 1.5 If
![]() $y \in \mathcal {I}_n$
and
$y \in \mathcal {I}_n$
and
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
where
![]() $\delta _{ij}$
denotes the usual Kronecker delta function.
$\delta _{ij}$
denotes the usual Kronecker delta function.
Example 1.6 The involution
![]() $y = 1432 = (2,4) \in \mathcal {I}_4$
has five reduced pipe dreams:
$y = 1432 = (2,4) \in \mathcal {I}_4$
has five reduced pipe dreams:
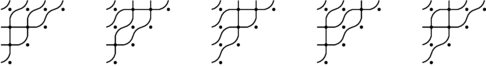
Only the last two of these are almost-symmetric, so
![]() $|\mathcal {ID}(y)| = 2$
and Theorem 1.5 reduces to the formula
$|\mathcal {ID}(y)| = 2$
and Theorem 1.5 reduces to the formula
![]() $\hat {\mathfrak {S}}_{y} = (x_2+x_1)(x_3+x_1) + (x_2+x_1)(x_2 + x_2)/2 = (x_2 + x_1)(x_3 + x_1 +x_2)$
. The monomial expansion has six terms, as opposed to two. In general, the expansion in Theorem 1.5 uses roughly a factor of
$\hat {\mathfrak {S}}_{y} = (x_2+x_1)(x_3+x_1) + (x_2+x_1)(x_2 + x_2)/2 = (x_2 + x_1)(x_3 + x_1 +x_2)$
. The monomial expansion has six terms, as opposed to two. In general, the expansion in Theorem 1.5 uses roughly a factor of
![]() $2^{\deg \hat {\mathfrak {S}}_y}$
fewer terms.
$2^{\deg \hat {\mathfrak {S}}_y}$
fewer terms.
Remark There is an alternate path toward establishing the fact that the class of a matrix Schubert variety is represented by the weighted sum of reduced pipe dreams. The defining ideal of
![]() $MX_w$
has a simple set of generators due to Fulton [Reference Fulton11]. Knutson and Miller showed that Fulton’s generators form a Gröbner basis with respect to any anti-diagonal term order [Reference Knutson and Miller23]. The Gröbner degeneration of this ideal decomposes into a union of coordinate subspaces indexed by reduced pipe dreams. Our hope is that a similar program can be implemented in the (skew-)symmetric setting, which would give a geometric proof of Theorem 1.5. We discuss this in greater detail in Section 6.2.
$MX_w$
has a simple set of generators due to Fulton [Reference Fulton11]. Knutson and Miller showed that Fulton’s generators form a Gröbner basis with respect to any anti-diagonal term order [Reference Knutson and Miller23]. The Gröbner degeneration of this ideal decomposes into a union of coordinate subspaces indexed by reduced pipe dreams. Our hope is that a similar program can be implemented in the (skew-)symmetric setting, which would give a geometric proof of Theorem 1.5. We discuss this in greater detail in Section 6.2.
In addition to Theorem 1.5, we also prove a number of results about the properties of involution pipe dreams. An outline of the rest of this article is as follows.
Section 2 contains some preliminaries on involution Schubert polynomials along with a proof of Theorem 1.2. In Section 3, we give several equivalent characterizations of
![]() $\mathcal {ID}(y)$
and
$\mathcal {ID}(y)$
and
![]() $\mathcal {FD}(z)$
in terms of reduced words for permutations. Section 4 contains our proof of Theorem 1.5, which uses ideas from recent work of Knutson [Reference Knutson22] along with certain transition equations for
$\mathcal {FD}(z)$
in terms of reduced words for permutations. Section 4 contains our proof of Theorem 1.5, which uses ideas from recent work of Knutson [Reference Knutson22] along with certain transition equations for
![]() $\hat {\mathfrak {S}}_y$
and
$\hat {\mathfrak {S}}_y$
and
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
given in [Reference Hamaker, Marberg and Pawlowski14]. In Section 5, we show that both families of involution pipe dreams are obtained from distinguished “bottom” elements by repeatedly applying certain simple transformations. These transformations are extensions of the ladder moves for pipe dreams described by Bergeron and Billey in [Reference Bergeron and Billey1]. In Section 6, finally, we describe several related open problems and conjectures.
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
given in [Reference Hamaker, Marberg and Pawlowski14]. In Section 5, we show that both families of involution pipe dreams are obtained from distinguished “bottom” elements by repeatedly applying certain simple transformations. These transformations are extensions of the ladder moves for pipe dreams described by Bergeron and Billey in [Reference Bergeron and Billey1]. In Section 6, finally, we describe several related open problems and conjectures.
2 Schubert polynomials and matrix varieties
Everywhere in this paper, n denotes a fixed positive integer. For convenience, we realize the symmetric group
![]() $S_n$
as the group of permutations of
$S_n$
as the group of permutations of
![]() $\mathbb {Z}_{>0} = \{1,2,3,\dots \}$
fixing all
$\mathbb {Z}_{>0} = \{1,2,3,\dots \}$
fixing all
![]() $i>n$
, so that there is an automatic inclusion
$i>n$
, so that there is an automatic inclusion
![]() $S_n \subset S_{n+1}$
. In this section, we present some relevant background on involution Schubert polynomials and equivariant cohomology, and then prove Theorem 1.2.
$S_n \subset S_{n+1}$
. In this section, we present some relevant background on involution Schubert polynomials and equivariant cohomology, and then prove Theorem 1.2.
2.1 Involution Schubert polynomials
To start, we provide a succinct definition of
![]() $\hat {\mathfrak {S}}_y$
and
$\hat {\mathfrak {S}}_y$
and
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
in terms of the ordinary Schubert polynomials
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
in terms of the ordinary Schubert polynomials
![]() $\mathfrak {S}_w$
given by (1.2). Let
$\mathfrak {S}_w$
given by (1.2). Let
![]() $s_i = (i,i+1) \in S_n$
for each
$s_i = (i,i+1) \in S_n$
for each
![]() $i \in [n-1]$
. A reduced word for
$i \in [n-1]$
. A reduced word for
![]() $w \in S_n$
is a minimal-length sequence
$w \in S_n$
is a minimal-length sequence
![]() $a_1a_2 \cdots a_l$
such that
$a_1a_2 \cdots a_l$
such that
![]() $w=s_{a_1}s_{a_2} \cdots s_{a_l}$
. Let
$w=s_{a_1}s_{a_2} \cdots s_{a_l}$
. Let
![]() $\mathcal {R}(w)$
denote the set of reduced words for w. The length
$\mathcal {R}(w)$
denote the set of reduced words for w. The length
![]() $\ell (w)$
of
$\ell (w)$
of
![]() $w \in S_n$
is the length of any word in
$w \in S_n$
is the length of any word in
![]() $\mathcal {R}(w)$
. One has
$\mathcal {R}(w)$
. One has
![]() $\ell (ws_i)=\ell (w)+1>\ell (w)$
if and only if
$\ell (ws_i)=\ell (w)+1>\ell (w)$
if and only if
![]() $w(i)< w(i+1)$
.
$w(i)< w(i+1)$
.
Proposition 2.1 [Reference Humphreys20, Theorem 7.1]
There is a unique associative operation
![]() $\circ : S_n \times S _n \to S_n$
, called the Demazure product, with
$\circ : S_n \times S _n \to S_n$
, called the Demazure product, with
![]() $s_i \circ s_i = s_i$
for all
$s_i \circ s_i = s_i$
for all
![]() $i \in [n-1]$
and
$i \in [n-1]$
and
![]() $v\circ w = vw$
for all
$v\circ w = vw$
for all
![]() $v,w \in S_n$
with
$v,w \in S_n$
with
![]() $\ell (vw) = \ell (v)+\ell (w)$
.
$\ell (vw) = \ell (v)+\ell (w)$
.
An involution word for
![]() $y \in \mathcal {I}_n = \{ w \in S_n : w=w^{-1}\}$
is a minimal-length word
$y \in \mathcal {I}_n = \{ w \in S_n : w=w^{-1}\}$
is a minimal-length word
![]() $a_1a_2 \cdots a_l$
with
$a_1a_2 \cdots a_l$
with
Note that we could replace
![]() $s_{a_1}\circ 1 \circ s_{a_1}$
in this expression by
$s_{a_1}\circ 1 \circ s_{a_1}$
in this expression by
![]() $s_{a_1} = s_{a_1}\circ s_{a_1}= s_{a_1}\circ 1 \circ s_{a_1}$
. An atom for
$s_{a_1} = s_{a_1}\circ s_{a_1}= s_{a_1}\circ 1 \circ s_{a_1}$
. An atom for
![]() $y \in \mathcal {I}_n$
is a minimal-length permutation
$y \in \mathcal {I}_n$
is a minimal-length permutation
![]() $w \in S_n$
with
$w \in S_n$
with
![]() $ y = w^{-1} \circ w. $
Let
$ y = w^{-1} \circ w. $
Let
![]() $\hat {\mathcal {R}}(y)$
be the set of involution words for
$\hat {\mathcal {R}}(y)$
be the set of involution words for
![]() $y \in \mathcal {I}_n$
and let
$y \in \mathcal {I}_n$
and let
![]() $\mathcal {A}(y)$
be the set of atoms for y. The associativity of the Demazure product implies that
$\mathcal {A}(y)$
be the set of atoms for y. The associativity of the Demazure product implies that
![]() $ \hat {\mathcal {R}}(y) = \bigsqcup _{w \in \mathcal {A}(y)} \mathcal {R}(w) $
.
$ \hat {\mathcal {R}}(y) = \bigsqcup _{w \in \mathcal {A}(y)} \mathcal {R}(w) $
.
Example 2.2 If
![]() $y = 1432 $
then
$y = 1432 $
then
![]() $\hat {\mathcal {R}}(y) = \{ 23, 32\}$
and
$\hat {\mathcal {R}}(y) = \{ 23, 32\}$
and
![]() $\mathcal {A}(y) = \{1342, 1423\}$
.
$\mathcal {A}(y) = \{1342, 1423\}$
.
One can show that
![]() $ \mathcal {I}_n = \{ w^{-1} \circ w : w \in S_n \} $
, so
$ \mathcal {I}_n = \{ w^{-1} \circ w : w \in S_n \} $
, so
![]() $\hat {\mathcal {R}}(y)$
and
$\hat {\mathcal {R}}(y)$
and
![]() $\mathcal {A}(y)$
are nonempty for all
$\mathcal {A}(y)$
are nonempty for all
![]() $y \in \mathcal {I}_n$
. Involution words are a special case of a more general construction of Richardson and Springer [Reference Richardson and Springer40], and have been studied by various authors [Reference Can, Joyce and Wyser5, Reference Hansson and Hultman15, Reference Hu and Zhang17, Reference Hultman18]. Our notation follows [Reference Hamaker, Marberg and Pawlowski12, Reference Hamaker, Marberg and Pawlowski13].
$y \in \mathcal {I}_n$
. Involution words are a special case of a more general construction of Richardson and Springer [Reference Richardson and Springer40], and have been studied by various authors [Reference Can, Joyce and Wyser5, Reference Hansson and Hultman15, Reference Hu and Zhang17, Reference Hultman18]. Our notation follows [Reference Hamaker, Marberg and Pawlowski12, Reference Hamaker, Marberg and Pawlowski13].
Definition 2.3 The involution Schubert polynomial of
![]() $y \in \mathcal {I}_n$
is
$y \in \mathcal {I}_n$
is
![]() $ \hat {\mathfrak {S}}_y = \sum _{w \in \mathcal {A}(y)} \mathfrak {S}_w. $
$ \hat {\mathfrak {S}}_y = \sum _{w \in \mathcal {A}(y)} \mathfrak {S}_w. $
Wyser and Yong [Reference Wyser and Yong45] originally defined these polynomials recursively using divided difference operators; work of Brion [Reference Brion4] implies that our definition agrees with theirs. For a detailed explanation of the equivalence among these definitions, see [Reference Hamaker, Marberg and Pawlowski13].
Example 2.4 If
![]() $z = 1432 \in \mathcal {I}_4$
then
$z = 1432 \in \mathcal {I}_4$
then
![]() $\mathcal {A}(z) = \{1342, 1423\}$
and
$\mathcal {A}(z) = \{1342, 1423\}$
and
Assume n is even, so
![]() $\mathcal {I}^{\mathsf {{FPF}}}_n = \{ z \in \mathcal {I}_n: i \neq z(i)\text { for all}\ i \in [n]\}$
is nonempty, and let
$\mathcal {I}^{\mathsf {{FPF}}}_n = \{ z \in \mathcal {I}_n: i \neq z(i)\text { for all}\ i \in [n]\}$
is nonempty, and let
An fpf-involution word for
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_{n}$
is a minimal-length word
$z \in \mathcal {I}^{\mathsf {{FPF}}}_{n}$
is a minimal-length word
![]() $a_1a_2 \cdots a_l$
with
$a_1a_2 \cdots a_l$
with
This formulation avoids the Demazure product, but there is an equivalent definition that more closely parallels (2.1). Namely, by [Reference Hamaker, Marberg and Pawlowski12, Corollary 2.6], an fpf-involution word for
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_{n}$
is also a minimal-length word
$z \in \mathcal {I}^{\mathsf {{FPF}}}_{n}$
is also a minimal-length word
![]() $a_1a_2 \cdots a_l$
with
$a_1a_2 \cdots a_l$
with
An fpf-atom for
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is a minimal length permutation
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is a minimal length permutation
![]() $w \in S_n$
with
$w \in S_n$
with
![]() $z = w^{-1} 1^{\mathsf {{FPF}}}_n w.$
Let
$z = w^{-1} 1^{\mathsf {{FPF}}}_n w.$
Let
![]() $\mathcal {A}^{\mathsf {{FPF}}}(z)$
be the set of fpf-atoms for z, and let
$\mathcal {A}^{\mathsf {{FPF}}}(z)$
be the set of fpf-atoms for z, and let
![]() $ \hat {\mathcal {R}}^{\mathsf {{FPF}}}(z) $
be the set of fpf-involution words for z. The basic properties of reduced words imply that
$ \hat {\mathcal {R}}^{\mathsf {{FPF}}}(z) $
be the set of fpf-involution words for z. The basic properties of reduced words imply that
Example 2.5 If
![]() $z = 4321 $
then
$z = 4321 $
then
![]() $\hat {\mathcal {R}}^{\mathsf {{FPF}}}(z) = \{ 23, 21\}$
and
$\hat {\mathcal {R}}^{\mathsf {{FPF}}}(z) = \{ 23, 21\}$
and
![]() $\mathcal {A}^{\mathsf {{FPF}}}(z) = \{1342, 3124\}$
.
$\mathcal {A}^{\mathsf {{FPF}}}(z) = \{1342, 3124\}$
.
Note that
![]() $a_1a_2\cdots a_l $
belongs to
$a_1a_2\cdots a_l $
belongs to
![]() $\hat {\mathcal {R}}^{\mathsf {{FPF}}}(z)$
if and only if
$\hat {\mathcal {R}}^{\mathsf {{FPF}}}(z)$
if and only if
![]() $135\cdots (n-1)a_1a_2\cdots a_l $
belongs to
$135\cdots (n-1)a_1a_2\cdots a_l $
belongs to
![]() $\hat {\mathcal {R}}(z)$
. If
$\hat {\mathcal {R}}(z)$
. If
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
![]() $\hat {\mathcal {R}}^{\mathsf {{FPF}}}(z) = \hat {\mathcal {R}}^{\mathsf {{FPF}}}(zs_{n+1}) $
and
$\hat {\mathcal {R}}^{\mathsf {{FPF}}}(z) = \hat {\mathcal {R}}^{\mathsf {{FPF}}}(zs_{n+1}) $
and
![]() $ \mathcal {A}^{\mathsf {{FPF}}}(z) = \mathcal {A}^{\mathsf {{FPF}}}(zs_{n+1}).$
$ \mathcal {A}^{\mathsf {{FPF}}}(z) = \mathcal {A}^{\mathsf {{FPF}}}(zs_{n+1}).$
Fpf-involution words are special cases of reduced words for quasiparabolic sets [Reference Rains and Vazirani39]. Since
![]() $\mathcal {I}^{\mathsf {{FPF}}}_n$
is a single
$\mathcal {I}^{\mathsf {{FPF}}}_n$
is a single
![]() $S_n$
-conjugacy class, each
$S_n$
-conjugacy class, each
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
has at least one fpf-involution word and fpf-atom.
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
has at least one fpf-involution word and fpf-atom.
Definition 2.6 The fpf-involution Schubert polynomial of
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is
These polynomials were also introduced in [Reference Wyser and Yong45]. If
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_{z} =\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_{zs_{n+1}}$
.
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_{z} =\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_{zs_{n+1}}$
.
Example 2.7 If
![]() $z = 532614 \in \mathcal {I}^{\mathsf {{FPF}}}_6$
then
$z = 532614 \in \mathcal {I}^{\mathsf {{FPF}}}_6$
then
![]() $\mathcal {A}^{\mathsf {{FPF}}}(z) = \{13452, 31254\}$
and
$\mathcal {A}^{\mathsf {{FPF}}}(z) = \{13452, 31254\}$
and
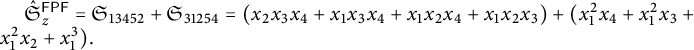 $ \hat {\mathfrak {S}}^{\mathsf {{FPF}}}_{z} = \mathfrak {S}_{13452} + \mathfrak {S}_{31254} = (x_2 x_3 x_4 + x_1 x_3 x_4 + x_1 x_2 x_4 + x_1 x_2 x_3) + (x_1^2 x_4 + x_1^2 x_3 + x_1^2 x_2 + x_1^3). $
$ \hat {\mathfrak {S}}^{\mathsf {{FPF}}}_{z} = \mathfrak {S}_{13452} + \mathfrak {S}_{31254} = (x_2 x_3 x_4 + x_1 x_3 x_4 + x_1 x_2 x_4 + x_1 x_2 x_3) + (x_1^2 x_4 + x_1^2 x_3 + x_1^2 x_2 + x_1^3). $
2.2 Torus-equivariant cohomology
Suppose V is a finite-dimensional rational representation of a torus
![]() $\mathsf {T} \simeq (\mathbb {C}^\times )^n$
. A character
$\mathsf {T} \simeq (\mathbb {C}^\times )^n$
. A character
![]() $\lambda \in \operatorname {Hom}(\mathsf {T}, \mathbb {C}^\times )$
is a weight of V if the weight space
$\lambda \in \operatorname {Hom}(\mathsf {T}, \mathbb {C}^\times )$
is a weight of V if the weight space
![]() $V_\lambda = \{v \in V : tv = \lambda (t)v\ \text {for all}\ t \in \mathsf {T}\}$
is nonzero. Any nonzero
$V_\lambda = \{v \in V : tv = \lambda (t)v\ \text {for all}\ t \in \mathsf {T}\}$
is nonzero. Any nonzero
![]() $v \in V_{\lambda }$
is a weight vector, and V has a basis of weight vectors. Let
$v \in V_{\lambda }$
is a weight vector, and V has a basis of weight vectors. Let
![]() $\operatorname {\mathrm {wt}}(V)$
denote the set of weights of V. After fixing an isomorphism
$\operatorname {\mathrm {wt}}(V)$
denote the set of weights of V. After fixing an isomorphism
![]() $\mathsf {T} \simeq (\mathbb {C}^\times )^n$
, we identify the character
$\mathsf {T} \simeq (\mathbb {C}^\times )^n$
, we identify the character
![]() $(t_1, \ldots , t_n) \mapsto t_1^{a_1} \cdots t_n^{a_n}$
with the linear polynomial
$(t_1, \ldots , t_n) \mapsto t_1^{a_1} \cdots t_n^{a_n}$
with the linear polynomial
![]() $a_1 x_1 + \cdots + a_n x_n \in \mathbb {Z}[x_1, \ldots , x_n]$
.
$a_1 x_1 + \cdots + a_n x_n \in \mathbb {Z}[x_1, \ldots , x_n]$
.
The equivariant cohomology ring
![]() $H_{\mathsf {T}}(V)$
is isomorphic to
$H_{\mathsf {T}}(V)$
is isomorphic to
![]() $\mathbb {Z}[x_1, \ldots , x_n]$
, an identification we make without comment from now on. Each
$\mathbb {Z}[x_1, \ldots , x_n]$
, an identification we make without comment from now on. Each
![]() $\mathsf {T}$
-invariant subscheme
$\mathsf {T}$
-invariant subscheme
![]() $X \subseteq V$
has an associated class
$X \subseteq V$
has an associated class
![]() $[X] \in H_{\mathsf {T}}(V)$
, which we describe following [Reference Miller and Sturmfels36, Chapter 8].
$[X] \in H_{\mathsf {T}}(V)$
, which we describe following [Reference Miller and Sturmfels36, Chapter 8].
First, if X is a linear subspace then we define
![]() $[X] = \prod _{\lambda \in \operatorname {\mathrm {wt}}(X)} \lambda $
, where we identify each character
$[X] = \prod _{\lambda \in \operatorname {\mathrm {wt}}(X)} \lambda $
, where we identify each character
![]() $\lambda $
with a linear polynomial as above. More generally, fix a basis of weight vectors of V, and let
$\lambda $
with a linear polynomial as above. More generally, fix a basis of weight vectors of V, and let
![]() $z_1, \ldots , z_n \in V^*$
be the dual basis; this determines an isomorphism
$z_1, \ldots , z_n \in V^*$
be the dual basis; this determines an isomorphism
![]() $\mathbb {C}[V] = \operatorname {Sym}(V^*) \simeq \mathbb {C}[z_1, \ldots , z_n]$
.
$\mathbb {C}[V] = \operatorname {Sym}(V^*) \simeq \mathbb {C}[z_1, \ldots , z_n]$
.
Choose a term order on monomials in
![]() $z_1, \ldots , z_n$
, and let
$z_1, \ldots , z_n$
, and let
![]() $\operatorname {\mathrm {\mathsf {init}}}(I)$
denote the ideal generated by the leading terms of all members of a given set
$\operatorname {\mathrm {\mathsf {init}}}(I)$
denote the ideal generated by the leading terms of all members of a given set
![]() $I \subseteq \mathbb {C}[V]$
. Given that
$I \subseteq \mathbb {C}[V]$
. Given that
![]() $\operatorname {\mathrm {\mathsf {init}}}(I)$
is a monomial ideal, one can show that each of its associated primes
$\operatorname {\mathrm {\mathsf {init}}}(I)$
is a monomial ideal, one can show that each of its associated primes
![]() $\mathfrak {p}$
is also a monomial ideal, and hence of the form
$\mathfrak {p}$
is also a monomial ideal, and hence of the form
![]() $\langle z_{i_1}, \ldots , z_{i_r} \rangle $
. The corresponding subscheme
$\langle z_{i_1}, \ldots , z_{i_r} \rangle $
. The corresponding subscheme
![]() $Z(\mathfrak {p})$
is a
$Z(\mathfrak {p})$
is a
![]() $\mathsf {T}$
-invariant linear subspace of V. Now define
$\mathsf {T}$
-invariant linear subspace of V. Now define
where
![]() $I(X)$
is the ideal of X and
$I(X)$
is the ideal of X and
![]() $\mathfrak {p}$
runs over the associated primes of
$\mathfrak {p}$
runs over the associated primes of
![]() $\operatorname {\mathrm {\mathsf {init}}} I(X)$
.
$\operatorname {\mathrm {\mathsf {init}}} I(X)$
.
2.3 Classes of involution matrix Schubert varieties
The matrix Schubert varieties in Theorem 1.1 can be described in terms of rank conditions, namely:
where
![]() $\mathsf {Mat}_n$
is the variety of
$\mathsf {Mat}_n$
is the variety of
![]() $n\times n$
matrices,
$n\times n$
matrices,
![]() $A_{[i][j]}$
denotes the upper-left
$A_{[i][j]}$
denotes the upper-left
![]() $i \times j$
corner of
$i \times j$
corner of
![]() $A \in \mathsf {Mat}_n$
, and we identify
$A \in \mathsf {Mat}_n$
, and we identify
![]() $w \in S_n$
with the
$w \in S_n$
with the
![]() $n\times n$
permutation matrix having
$n\times n$
permutation matrix having
![]() $1$
’s in positions
$1$
’s in positions
![]() $(i,w(i))$
.
$(i,w(i))$
.
The varieties
![]() $M\hat X_y$
and
$M\hat X_y$
and
![]() $M\hat X^{\mathsf {{FPF}}}_z$
from Theorem 1.2 can be reformulated in a similar way. Specifically, we define the involution matrix Schubert variety of
$M\hat X^{\mathsf {{FPF}}}_z$
from Theorem 1.2 can be reformulated in a similar way. Specifically, we define the involution matrix Schubert variety of
![]() $y \in \mathcal {I}_n$
by
$y \in \mathcal {I}_n$
by
 $$ \begin{align} M\hat X_y &= MX_y \cap \mathsf{SMat}_n \nonumber\\&= \{A \in \mathsf{SMat}_n : \operatorname{\mathrm{rank}} A_{[i][j]} \leq \operatorname{\mathrm{rank}} y_{[i][j]}\ \text{for}\ i,j \in [n]\}, \end{align} $$
$$ \begin{align} M\hat X_y &= MX_y \cap \mathsf{SMat}_n \nonumber\\&= \{A \in \mathsf{SMat}_n : \operatorname{\mathrm{rank}} A_{[i][j]} \leq \operatorname{\mathrm{rank}} y_{[i][j]}\ \text{for}\ i,j \in [n]\}, \end{align} $$
where
![]() $\mathsf {SMat}_n$
is the subvariety of symmetric matrices in
$\mathsf {SMat}_n$
is the subvariety of symmetric matrices in
![]() $\mathsf {Mat}_n$
. When n is even, we define the fpf-involution matrix Schubert variety of
$\mathsf {Mat}_n$
. When n is even, we define the fpf-involution matrix Schubert variety of
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
by
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
by
 $$ \begin{align} M\hat X^{\mathsf{{FPF}}}_z &= MX_z \cap \mathsf{SSMat}_n \nonumber\\&= \{A \in \mathsf{SSMat}_n : \operatorname{\mathrm{rank}} A_{[i][j]} \leq \operatorname{\mathrm{rank}} z_{[i][j]}\ \text{for}\ i,j \in [n]\}, \end{align} $$
$$ \begin{align} M\hat X^{\mathsf{{FPF}}}_z &= MX_z \cap \mathsf{SSMat}_n \nonumber\\&= \{A \in \mathsf{SSMat}_n : \operatorname{\mathrm{rank}} A_{[i][j]} \leq \operatorname{\mathrm{rank}} z_{[i][j]}\ \text{for}\ i,j \in [n]\}, \end{align} $$
where
![]() $\mathsf {SSMat}_n$
is the subvariety of skew-symmetric matrices in
$\mathsf {SSMat}_n$
is the subvariety of skew-symmetric matrices in
![]() $\mathsf {Mat}_n$
.
$\mathsf {Mat}_n$
.
Example 2.8 Suppose
![]() $y = 132 =\left [\begin {smallmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end {smallmatrix}\right ]\in \mathcal {I}_3$
. Setting
$y = 132 =\left [\begin {smallmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end {smallmatrix}\right ]\in \mathcal {I}_3$
. Setting
![]() $R_{ij} = \operatorname {\mathrm {rank}} y_{[i][j]}$
, we have
$R_{ij} = \operatorname {\mathrm {rank}} y_{[i][j]}$
, we have
![]() $R = \left [\begin {smallmatrix} 1 & 1 & 1 \\ 1 & 1 & 2\\ 1 & 2 & 3 \end {smallmatrix}\right ]$
. The conditions
$R = \left [\begin {smallmatrix} 1 & 1 & 1 \\ 1 & 1 & 2\\ 1 & 2 & 3 \end {smallmatrix}\right ]$
. The conditions
![]() $\operatorname {\mathrm {rank}} A_{[i][j]} \leq R_{ij}$
for
$\operatorname {\mathrm {rank}} A_{[i][j]} \leq R_{ij}$
for
![]() $i,j \in [3]$
defining
$i,j \in [3]$
defining
![]() $M\hat X_y$
are all implied by the single condition
$M\hat X_y$
are all implied by the single condition
![]() $\operatorname {\mathrm {rank}} A_{[2][2]} \leq R_{22} = 1$
. Thus,
$\operatorname {\mathrm {rank}} A_{[2][2]} \leq R_{22} = 1$
. Thus,
Let
![]() $\mathsf {T} \subseteq \mathsf {GL}_n$
be the usual torus of invertible diagonal matrices. Recall that
$\mathsf {T} \subseteq \mathsf {GL}_n$
be the usual torus of invertible diagonal matrices. Recall that
![]() $\kappa (y) = |\{ i : y(i) < i\}|$
for
$\kappa (y) = |\{ i : y(i) < i\}|$
for
![]() $y \in \mathcal {I}_n$
, and that
$y \in \mathcal {I}_n$
, and that
![]() $ \mathsf {T}$
acts on matrices in
$ \mathsf {T}$
acts on matrices in
![]() $ \mathsf {Mat}_n$
by
$ \mathsf {Mat}_n$
by
![]() $t\cdot A = tA$
and on symmetric matrices in
$t\cdot A = tA$
and on symmetric matrices in
![]() $ \mathsf {SMat}_n$
by
$ \mathsf {SMat}_n$
by
![]() $t \cdot A = tAt$
. We can now prove Theorem 1.2, which states that if
$t \cdot A = tAt$
. We can now prove Theorem 1.2, which states that if
![]() $y \in \mathcal {I}_n$
and
$y \in \mathcal {I}_n$
and
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
![]() $2^{\kappa (y)}\hat {\mathfrak {S}}_y = [M\hat X_y] \in H_{\mathsf {T}}^*(\mathsf {SMat}_n)$
while
$2^{\kappa (y)}\hat {\mathfrak {S}}_y = [M\hat X_y] \in H_{\mathsf {T}}^*(\mathsf {SMat}_n)$
while
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z = [M\hat X^{\mathsf {{FPF}}}_z] \in H_{\mathsf {T}}^*(\mathsf {SSMat}_n)$
.
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z = [M\hat X^{\mathsf {{FPF}}}_z] \in H_{\mathsf {T}}^*(\mathsf {SSMat}_n)$
.
Remark It is possible, though a little cumbersome, to derive Theorem 1.2 from [Reference Marberg and Pawlowski31, Theorem 2.17 and Lemma 3.1], which provide a similar statement in complex K-theory. We originally announced Theorem 1.2 in an extended abstract for this paper which preceded the appearance of [Reference Marberg and Pawlowski31]. However, as the argument below is similar to the proofs of the results in [Reference Marberg and Pawlowski31], we will be somewhat curt here in our presentation of the details.
For
![]() $w = w_1 \dots w_n \in S_n$
, let
$w = w_1 \dots w_n \in S_n$
, let
![]() $w \times 1^k = w_1 \dots w_n\ n{+}1 \dots n{+}k \in S_{n+k}$
. Similarly, for n even define
$w \times 1^k = w_1 \dots w_n\ n{+}1 \dots n{+}k \in S_{n+k}$
. Similarly, for n even define
![]() $w \times (21)^k = w \times 1^{2k} \cdot (1^{\mathsf {{FPF}}}_n \cdot 1^{\mathsf {{FPF}}}_{n+2k})$
. Our proof of Theorem 1.2 relies on the following characterizations of
$w \times (21)^k = w \times 1^{2k} \cdot (1^{\mathsf {{FPF}}}_n \cdot 1^{\mathsf {{FPF}}}_{n+2k})$
. Our proof of Theorem 1.2 relies on the following characterizations of
![]() $\hat {\mathfrak {S}}_y$
and
$\hat {\mathfrak {S}}_y$
and
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
:
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
:
Theorem 2.9 [Reference Wyser and Yong45, Theorem 2]
If
![]() $y \in \mathcal {I}_n$
and
$y \in \mathcal {I}_n$
and
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
, then
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
, then
![]() $2^{\kappa (y)}\hat {\mathfrak {S}}_y$
and
$2^{\kappa (y)}\hat {\mathfrak {S}}_y$
and
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
are the unique representatives for
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
are the unique representatives for
![]() $[\hat X_y]$
and
$[\hat X_y]$
and
![]() $[\hat X^{\mathsf {{FPF}}}_z]$
with
$[\hat X^{\mathsf {{FPF}}}_z]$
with
![]() $2^{\kappa (y)}\hat {\mathfrak {S}}_y = 2^{\kappa (y)}\hat {\mathfrak {S}}_{y\times 1^k}$
and
$2^{\kappa (y)}\hat {\mathfrak {S}}_y = 2^{\kappa (y)}\hat {\mathfrak {S}}_{y\times 1^k}$
and
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z = \hat {\mathfrak {S}}^{\mathsf {{FPF}}}_{z \times (21)^k}$
for all
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z = \hat {\mathfrak {S}}^{\mathsf {{FPF}}}_{z \times (21)^k}$
for all
![]() $k \geq 1$
.
$k \geq 1$
.
Proof of Theorem 1.2 If X and Y are complex varieties with
![]() $\mathsf {T}$
-actions, and
$\mathsf {T}$
-actions, and
![]() $f : X \to Y$
is a
$f : X \to Y$
is a
![]() $\mathsf {T}$
-equivariant morphism, then there is a pullback homomorphism
$\mathsf {T}$
-equivariant morphism, then there is a pullback homomorphism
![]() $f^* : H_{\mathsf {T}}^*(Y) \to H_{\mathsf {T}}^*(X)$
. If f is a flat morphism (e.g., an inclusion of an open subset, a projection of a fiber bundle, or a composition of flat morphisms), then
$f^* : H_{\mathsf {T}}^*(Y) \to H_{\mathsf {T}}^*(X)$
. If f is a flat morphism (e.g., an inclusion of an open subset, a projection of a fiber bundle, or a composition of flat morphisms), then
![]() $f^*([Z]) = [f^{-1}(Z)]$
for any subscheme
$f^*([Z]) = [f^{-1}(Z)]$
for any subscheme
![]() $Z \subseteq Y$
.
$Z \subseteq Y$
.
Because
![]() $\mathsf {T}$
acts freely on
$\mathsf {T}$
acts freely on
![]() $\mathsf {GL}_n$
and since
$\mathsf {GL}_n$
and since
![]() $\mathsf {T}\backslash \mathsf {GL}_n \twoheadrightarrow \mathsf {B} \backslash \mathsf {GL}_n \simeq \mathsf {Fl}_{n}$
is a homotopy equivalence (see, e.g., [Reference McGovern35, Section 8.1]), one has
$\mathsf {T}\backslash \mathsf {GL}_n \twoheadrightarrow \mathsf {B} \backslash \mathsf {GL}_n \simeq \mathsf {Fl}_{n}$
is a homotopy equivalence (see, e.g., [Reference McGovern35, Section 8.1]), one has
![]() $H_{\mathsf {T}}^*(\mathsf {GL}_n) \simeq H^*(\mathsf {T} \backslash \mathsf {GL}_n) \simeq H^*(\mathsf {Fl}_{n})$
. If
$H_{\mathsf {T}}^*(\mathsf {GL}_n) \simeq H^*(\mathsf {T} \backslash \mathsf {GL}_n) \simeq H^*(\mathsf {Fl}_{n})$
. If
![]() $Z \subseteq \mathsf {GL}_n$
is a
$Z \subseteq \mathsf {GL}_n$
is a
![]() $\mathsf {B}$
-invariant subvariety, then
$\mathsf {B}$
-invariant subvariety, then
![]() $[Z] \in H_{\mathsf {T}}^*(\mathsf {GL}_n)$
corresponds to the class of
$[Z] \in H_{\mathsf {T}}^*(\mathsf {GL}_n)$
corresponds to the class of
![]() $\mathsf {B}\backslash Z = \{\mathsf {B} g : g \in Z\}$
in
$\mathsf {B}\backslash Z = \{\mathsf {B} g : g \in Z\}$
in
![]() $H^*(\mathsf {Fl}_{n})$
. Fix
$H^*(\mathsf {Fl}_{n})$
. Fix
![]() $y \in \mathcal {I}_n$
and define
$y \in \mathcal {I}_n$
and define
![]() $\sigma : \mathsf {GL}_n \to \mathsf {SMat}_n$
by
$\sigma : \mathsf {GL}_n \to \mathsf {SMat}_n$
by
![]() $\sigma (g) = gg^T$
. Let
$\sigma (g) = gg^T$
. Let
![]() $\iota : \mathsf {GL}_n \hookrightarrow M_n$
be the obvious inclusion and consider the diagram
$\iota : \mathsf {GL}_n \hookrightarrow M_n$
be the obvious inclusion and consider the diagram

Realize
![]() $\mathsf {O}_n$
as the group
$\mathsf {O}_n$
as the group
![]() $\{g \in \mathsf {GL}_n : gg^T = 1\}$
. The map
$\{g \in \mathsf {GL}_n : gg^T = 1\}$
. The map
![]() $\sigma $
is flat because it is the composition
$\sigma $
is flat because it is the composition
![]() $\mathsf {GL}_n \twoheadrightarrow \mathsf {GL}_n/\mathsf {O}_n \hookrightarrow \mathsf {SMat}_n$
, where the second map sends
$\mathsf {GL}_n \twoheadrightarrow \mathsf {GL}_n/\mathsf {O}_n \hookrightarrow \mathsf {SMat}_n$
, where the second map sends
![]() $g\mathsf {O}_n \mapsto gg^T$
and may be identified with the open inclusion
$g\mathsf {O}_n \mapsto gg^T$
and may be identified with the open inclusion
![]() $\mathsf {GL}_n \cap \mathsf {SMat}_n \hookrightarrow \mathsf {SMat}_n$
. For fixed
$\mathsf {GL}_n \cap \mathsf {SMat}_n \hookrightarrow \mathsf {SMat}_n$
. For fixed
![]() $i \in [n]$
, one checks using the prescription of Section 2.2 that
$i \in [n]$
, one checks using the prescription of Section 2.2 that
![]() $2x_i$
represents both the class of
$2x_i$
represents both the class of
![]() $Z = \{A \in \mathsf {SMat}_n : A_{ii} = 0\}$
in
$Z = \{A \in \mathsf {SMat}_n : A_{ii} = 0\}$
in
![]() $H_{\mathsf {T}}^*(\mathsf {SMat}_n)$
and the class of
$H_{\mathsf {T}}^*(\mathsf {SMat}_n)$
and the class of
![]() $Z' = \{A \in M_n : (AA^T)_{ii} = 0\}$
in
$Z' = \{A \in M_n : (AA^T)_{ii} = 0\}$
in
![]() $H_{\mathsf {T}}^*(M_n)$
. Since
$H_{\mathsf {T}}^*(M_n)$
. Since
![]() $\sigma ^*[Z] = [\sigma ^{-1}(Z)] = [\iota ^{-1}(Z')] = \iota ^*[Z']$
, this calculation implies that (2.5) commutes.
$\sigma ^*[Z] = [\sigma ^{-1}(Z)] = [\iota ^{-1}(Z')] = \iota ^*[Z']$
, this calculation implies that (2.5) commutes.
Now set
![]() $ \hat X_y = \mathsf {B} \backslash \sigma ^{-1}(M\hat X_y) = \{\mathsf {B} g \in \mathsf {Fl}_{n} : \operatorname {\mathrm {rank}} (gg^T)_{[i][j]} \leq \operatorname {\mathrm {rank}} y_{[i][j]} \text { for}\ i,j \in [n]\},$
so that the path through the upper-left corner of (2.5) sends the polynomial
$ \hat X_y = \mathsf {B} \backslash \sigma ^{-1}(M\hat X_y) = \{\mathsf {B} g \in \mathsf {Fl}_{n} : \operatorname {\mathrm {rank}} (gg^T)_{[i][j]} \leq \operatorname {\mathrm {rank}} y_{[i][j]} \text { for}\ i,j \in [n]\},$
so that the path through the upper-left corner of (2.5) sends the polynomial
![]() $[M\hat X_y]$
to
$[M\hat X_y]$
to
![]() $[\hat X_y]$
. The variety
$[\hat X_y]$
. The variety
![]() $\hat X_y$
is the closure of an
$\hat X_y$
is the closure of an
![]() $\mathsf {O}_n$
-orbit on
$\mathsf {O}_n$
-orbit on
![]() $\mathsf {Fl}_{n}$
[Reference Wyser44, Section 2.1.2]. The path through the lower-right corner of (2.5) is simply the classical Borel map
$\mathsf {Fl}_{n}$
[Reference Wyser44, Section 2.1.2]. The path through the lower-right corner of (2.5) is simply the classical Borel map
![]() $\mathbb {Z}[x_1, \ldots , x_n] \to H^*(\mathsf {Fl}_{n})$
. We claim
$\mathbb {Z}[x_1, \ldots , x_n] \to H^*(\mathsf {Fl}_{n})$
. We claim
![]() $[M\hat X_{y \times 1^m}]$
is constant for fixed y and varying m. Since
$[M\hat X_{y \times 1^m}]$
is constant for fixed y and varying m. Since
![]() $[M\hat X_{y}]$
is a representative for
$[M\hat X_{y}]$
is a representative for
![]() $[\hat X_y]$
, the result then follows by Theorem 2.9.
$[\hat X_y]$
, the result then follows by Theorem 2.9.
For
![]() $y \neq 1 \in S_n$
, define
$y \neq 1 \in S_n$
, define
![]() $\operatorname {maxdes}(y) = \max \{i \in \mathbb {Z}_{\geq 0} : y(i)> y(i+1)\}$
. Replacing
$\operatorname {maxdes}(y) = \max \{i \in \mathbb {Z}_{\geq 0} : y(i)> y(i+1)\}$
. Replacing
![]() $[n]$
in the definition (2.3) by
$[n]$
in the definition (2.3) by
![]() $[\operatorname {maxdes}(y)]$
yields exactly the same variety
$[\operatorname {maxdes}(y)]$
yields exactly the same variety
![]() $M\hat X_y$
. Since
$M\hat X_y$
. Since
![]() $\operatorname {maxdes}(y \times 1^m)$
is independent of m, as is
$\operatorname {maxdes}(y \times 1^m)$
is independent of m, as is
![]() $\operatorname {\mathrm {rank}}(y \times 1^m)_{[i][j]}$
for
$\operatorname {\mathrm {rank}}(y \times 1^m)_{[i][j]}$
for
![]() $i, j \in [\operatorname {maxdes}(y)]$
, it follows that the ideals of
$i, j \in [\operatorname {maxdes}(y)]$
, it follows that the ideals of
![]() $M\hat X_{y \times 1^m}$
for fixed y and varying m have a common generating set. It is clear from §2.2 that this means that the polynomial
$M\hat X_{y \times 1^m}$
for fixed y and varying m have a common generating set. It is clear from §2.2 that this means that the polynomial
![]() $[M\hat X_{y \times 1^m}]$
is independent of m.
$[M\hat X_{y \times 1^m}]$
is independent of m.
The proof for the skew-symmetric case is the same, replacing
![]() $\mathsf {O}_n$
by
$\mathsf {O}_n$
by
![]() $\mathsf {Sp}_n$
and the map
$\mathsf {Sp}_n$
and the map
![]() $\sigma : g \mapsto gg^T$
by
$\sigma : g \mapsto gg^T$
by
![]() $g \mapsto g\Omega g^T$
, where
$g \mapsto g\Omega g^T$
, where
![]() $\Omega \in \mathsf {GL}_n$
is the nondegenerate skew-symmetric form preserved by
$\Omega \in \mathsf {GL}_n$
is the nondegenerate skew-symmetric form preserved by
![]() $\mathsf {Sp}_n$
.
$\mathsf {Sp}_n$
.
Corollary 2.10 The polynomial
![]() $2^{\kappa (y)}\hat {\mathfrak {S}}_y$
(respectively,
$2^{\kappa (y)}\hat {\mathfrak {S}}_y$
(respectively,
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
) is a positive integer linear combination of products of terms
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
) is a positive integer linear combination of products of terms
![]() $x_i+x_j$
for
$x_i+x_j$
for
![]() $1 \leq i \leq j \leq n$
(respectively,
$1 \leq i \leq j \leq n$
(respectively,
![]() $1 \leq i < j \leq n$
).
$1 \leq i < j \leq n$
).
Proof The weights of
![]() $\mathsf {T}$
acting on
$\mathsf {T}$
acting on
![]() $\mathsf {SMat}_n$
are
$\mathsf {SMat}_n$
are
![]() $x_i+x_j$
for
$x_i+x_j$
for
![]() $1 \leq i \leq j \leq n$
, while the weights of
$1 \leq i \leq j \leq n$
, while the weights of
![]() $\mathsf {SSMat}_n$
are the same with the added restriction
$\mathsf {SSMat}_n$
are the same with the added restriction
![]() $i < j$
. The expression (2.2) makes clear that the classes
$i < j$
. The expression (2.2) makes clear that the classes
![]() $[M\hat X_y]$
and
$[M\hat X_y]$
and
![]() $[M\hat X^{\mathsf {{FPF}}}_z]$
are positive integer linear combinations of products of these weights.▪
$[M\hat X^{\mathsf {{FPF}}}_z]$
are positive integer linear combinations of products of these weights.▪
Remark Let
![]() $\mathsf {S}$
be a maximal torus in
$\mathsf {S}$
be a maximal torus in
![]() $\mathsf {O}_n$
. Let
$\mathsf {O}_n$
. Let
![]() $\mathsf {T} \times \mathsf {S}$
act on
$\mathsf {T} \times \mathsf {S}$
act on
![]() $\mathsf {GL}_n$
by
$\mathsf {GL}_n$
by
![]() $(t,s) \cdot g = tgs^{-1}$
and on
$(t,s) \cdot g = tgs^{-1}$
and on
![]() $\mathsf {SMat}_n$
by
$\mathsf {SMat}_n$
by
![]() $(t,s) \cdot A = tAt$
. The map
$(t,s) \cdot A = tAt$
. The map
![]() $\sigma : \mathsf {GL}_n \to \mathsf {SMat}_n$
,
$\sigma : \mathsf {GL}_n \to \mathsf {SMat}_n$
,
![]() $g \mapsto gg^T$
considered above is then
$g \mapsto gg^T$
considered above is then
![]() $\mathsf {T} \times \mathsf {S}$
-equivariant. Since the second factor of
$\mathsf {T} \times \mathsf {S}$
-equivariant. Since the second factor of
![]() $\mathsf {T} \times \mathsf {S}$
acts trivially on
$\mathsf {T} \times \mathsf {S}$
acts trivially on
![]() $\mathsf {SMat}_n$
, the polynomial
$\mathsf {SMat}_n$
, the polynomial
![]() $2^{\kappa (y)}\hat {\mathfrak {S}}_y$
still represents the class
$2^{\kappa (y)}\hat {\mathfrak {S}}_y$
still represents the class
![]() $[M\hat X_y] \in H_{\mathsf {T} \times \mathsf {S}}(\mathsf {SMat}_n)$
. It follows as in the proof of Theorem 1.2 that
$[M\hat X_y] \in H_{\mathsf {T} \times \mathsf {S}}(\mathsf {SMat}_n)$
. It follows as in the proof of Theorem 1.2 that
![]() $2^{\kappa (y)}\hat {\mathfrak {S}}_y$
also represents the class
$2^{\kappa (y)}\hat {\mathfrak {S}}_y$
also represents the class
![]() $[\hat X_y]_{\mathsf {S}} \in H_{\mathsf {S}}(\mathsf {Fl}_{n})$
. The latter fact was proven by Wyser and Yong [Reference Wyser and Yong45], but our approach gives an explanation for the surprising existence of a representative for
$[\hat X_y]_{\mathsf {S}} \in H_{\mathsf {S}}(\mathsf {Fl}_{n})$
. The latter fact was proven by Wyser and Yong [Reference Wyser and Yong45], but our approach gives an explanation for the surprising existence of a representative for
![]() $[\hat X_y]_{\mathsf {S}}$
not involving the
$[\hat X_y]_{\mathsf {S}}$
not involving the
![]() $\mathsf {S}$
-weights. Similar remarks apply in the skew-symmetric case.
$\mathsf {S}$
-weights. Similar remarks apply in the skew-symmetric case.
3 Characterizing pipe dreams
The rest of this article is focused on the combinatorial properties of involution pipe dreams and their role in the formulas in Theorem 1.5 that manifest Corollary 2.10. In the introduction, we defined (fpf-)involution pipe dreams via simple symmetry conditions. In this section, we give an equivalent characterization in terms of “compatible sequences” related to involution words.
3.1 Reading words
For
![]() $p \in \mathbb {Z}$
, the
$p \in \mathbb {Z}$
, the
![]() $p{th}$
antidiagonal in
$p{th}$
antidiagonal in
![]() $\mathbb {Z}_{>0} \times \mathbb {Z}_{>0}$
is the set
$\mathbb {Z}_{>0} \times \mathbb {Z}_{>0}$
is the set
The
![]() $p{th}$
diagonal in
$p{th}$
diagonal in
![]() $\mathbb {Z}_{>0} \times \mathbb {Z}_{>0}$
is the set
$\mathbb {Z}_{>0} \times \mathbb {Z}_{>0}$
is the set
Labeling the elements of
![]() $\{1,2,3\}\times \{1,2,3\}$
by their antidiagonal and diagonal gives
$\{1,2,3\}\times \{1,2,3\}$
by their antidiagonal and diagonal gives
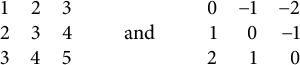 $$ \begin{align*} \begin{array}{ccc} 1 & 2 & 3\\ 2 & 3 & 4\\ 3 & 4 & 5\\ \end{array} \qquad \text{and} \qquad \begin{array}{rrr} 0 & -1 & -2\\ 1 & 0 & -1\\ 2 & 1 & 0 \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ccc} 1 & 2 & 3\\ 2 & 3 & 4\\ 3 & 4 & 5\\ \end{array} \qquad \text{and} \qquad \begin{array}{rrr} 0 & -1 & -2\\ 1 & 0 & -1\\ 2 & 1 & 0 \end{array} \end{align*} $$
respectively. Let
![]() $\mathsf {adiag}: \mathbb {Z}_{>0}\times \mathbb {Z}_{>0} \to \mathbb {Z}_{>0}$
be the map sending
$\mathsf {adiag}: \mathbb {Z}_{>0}\times \mathbb {Z}_{>0} \to \mathbb {Z}_{>0}$
be the map sending
![]() $(i,j) \mapsto i+j-1$
.
$(i,j) \mapsto i+j-1$
.
Definition 3.1 The standard reading word of
![]() $D\subseteq [n]\times [n]$
is the sequence
$D\subseteq [n]\times [n]$
is the sequence
where
![]() $\alpha _1,\alpha _2,\dots ,\alpha _{|D|}$
are the positions of D read row-by-row from right to left, starting with the top row.
$\alpha _1,\alpha _2,\dots ,\alpha _{|D|}$
are the positions of D read row-by-row from right to left, starting with the top row.
If one also records the row indices of the positions
![]() $\alpha _i$
as a second word, then the resulting words uniquely determine D and are the same data as a compatible sequence for
$\alpha _i$
as a second word, then the resulting words uniquely determine D and are the same data as a compatible sequence for
![]() $\mathsf {word}(D)$
(see [Reference Billey, Jockusch and Stanley3, (1)]).
$\mathsf {word}(D)$
(see [Reference Billey, Jockusch and Stanley3, (1)]).
Example 3.2 The subset
![]() $D= \{ (1,3),(1,2),(2,3),(2,2),(3,2)\}$
has
$D= \{ (1,3),(1,2),(2,3),(2,2),(3,2)\}$
has
![]() $\mathsf {word}(D) = 32434$
.
$\mathsf {word}(D) = 32434$
.
We introduce a more general class of reading words. Suppose
![]() $\omega : [n] \times [n] \to [n^2]$
is a bijection. For a subset
$\omega : [n] \times [n] \to [n^2]$
is a bijection. For a subset
![]() $D \subseteq [n] \times [n]$
with
$D \subseteq [n] \times [n]$
with
![]() $\omega (D) = \{ i_1 < i_2< \dots < i_{m}\}$
, let
$\omega (D) = \{ i_1 < i_2< \dots < i_{m}\}$
, let
The standard reading word of
![]() $D\subseteq [n]\times [n]$
corresponds to
$D\subseteq [n]\times [n]$
corresponds to
![]() $\omega : (i,j) \mapsto ni - j + 1$
.
$\omega : (i,j) \mapsto ni - j + 1$
.
Example 3.3 If
![]() $n=2$
and
$n=2$
and
![]() $\omega $
is such that
$\omega $
is such that
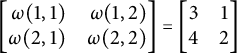 $ \left [ \begin {array}{@{}rr@{}} \omega (1,1) & \omega (1,2) \\ \omega (2,1) & \omega (2,2) \end {array}\right ] = \left [ \begin {array}{@{}cc@{}} 3 & 1 \\ 4 & 2 \end {array} \right ] $
then we would have
$ \left [ \begin {array}{@{}rr@{}} \omega (1,1) & \omega (1,2) \\ \omega (2,1) & \omega (2,2) \end {array}\right ] = \left [ \begin {array}{@{}cc@{}} 3 & 1 \\ 4 & 2 \end {array} \right ] $
then we would have
![]() $\mathsf {word}([n]\times [n],\omega ) = 2312$
, while if
$\mathsf {word}([n]\times [n],\omega ) = 2312$
, while if
![]() $D = \{(1,1),(2,2)\}$
then
$D = \{(1,1),(2,2)\}$
then
![]() $\mathsf {word} (D,\omega ) = 31$
.
$\mathsf {word} (D,\omega ) = 31$
.
For us, a linear extension of a finite poset
![]() $(P,\preceq )$
with size
$(P,\preceq )$
with size
![]() $m=|P|$
is a bijection
$m=|P|$
is a bijection
![]() $\omega : P \to [m]$
such that
$\omega : P \to [m]$
such that
![]() $\omega (s) < \omega (t)$
whenever
$\omega (s) < \omega (t)$
whenever
![]() $s \prec t$
in P.
$s \prec t$
in P.
Definition 3.4 A reading order on
![]() $[n]\times [n]$
is a linear extension of the partial order
$[n]\times [n]$
is a linear extension of the partial order
![]() $\leq _{\mathsf {NE}}$
on
$\leq _{\mathsf {NE}}$
on
![]() $[n] \times [n]$
that has
$[n] \times [n]$
that has
![]() $(i,j) \leq _{\mathsf {NE}} (i',j')$
if and only if both
$(i,j) \leq _{\mathsf {NE}} (i',j')$
if and only if both
![]() $i \leq i'$
and
$i \leq i'$
and
![]() $j \geq j'$
. If
$j \geq j'$
. If
![]() $\omega $
is a reading order, then we refer to
$\omega $
is a reading order, then we refer to
![]() $\mathsf {word}(D,\omega )$
as a reading word of
$\mathsf {word}(D,\omega )$
as a reading word of
![]() $D\subseteq [n]\times [n]$
.
$D\subseteq [n]\times [n]$
.
The Coxeter commutation class of a finite sequence of integers is its equivalence class under the relation that lets adjacent letters commute if their positive difference is at least two. For example,
![]() $\{1324, 3124,1342,3142, 3412\}$
is a single Coxeter commutation class. Fix a set
$\{1324, 3124,1342,3142, 3412\}$
is a single Coxeter commutation class. Fix a set
![]() $D \subseteq [n] \times [n]$
.
$D \subseteq [n] \times [n]$
.
Lemma 3.5 All reading words of D are in the same Coxeter commutation class.
This result can be derived using Viennot’s theory of heaps of pieces; see [Reference Viennot43, Lemma 3.3].
Proof Let
![]() $s_p \in S_{n^2}$
be the simple transposition interchanging p and
$s_p \in S_{n^2}$
be the simple transposition interchanging p and
![]() $p+1$
, and choose a reading order
$p+1$
, and choose a reading order
![]() $\omega $
on
$\omega $
on
![]() $[n]\times [n]$
. The sequence
$[n]\times [n]$
. The sequence
![]() $\mathsf {word}(D, s_p \omega )$
is equal to
$\mathsf {word}(D, s_p \omega )$
is equal to
![]() $\mathsf {word}(D, \omega )$
when
$\mathsf {word}(D, \omega )$
when
![]() $\{p,p+1\}\not \subset \omega (D)$
, and otherwise is obtained by interchanging two adjacent letters in
$\{p,p+1\}\not \subset \omega (D)$
, and otherwise is obtained by interchanging two adjacent letters in
![]() $\mathsf {word}(D,\omega )$
. In the latter case, if
$\mathsf {word}(D,\omega )$
. In the latter case, if
![]() $\omega ^{-1}(p) = (i,j)$
and
$\omega ^{-1}(p) = (i,j)$
and
![]() $\omega ^{-1}(p+1) = (i',j')$
are not in adjacent antidiagonals, then
$\omega ^{-1}(p+1) = (i',j')$
are not in adjacent antidiagonals, then
![]() $\mathsf {word}(D,\omega )$
and
$\mathsf {word}(D,\omega )$
and
![]() $\mathsf {word}(D, s_p \omega )$
are in the same Coxeter commutation class.
$\mathsf {word}(D, s_p \omega )$
are in the same Coxeter commutation class.
Now suppose
![]() $\upsilon $
is a second reading order on
$\upsilon $
is a second reading order on
![]() $[n]\times [n]$
. We claim that one can pass from
$[n]\times [n]$
. We claim that one can pass from
![]() $\omega $
to
$\omega $
to
![]() $\upsilon $
by composing
$\upsilon $
by composing
![]() $\omega $
with a sequence of simple transpositions obeying the condition just described. To check this, we induct on the number of inversions in the permutation
$\omega $
with a sequence of simple transpositions obeying the condition just described. To check this, we induct on the number of inversions in the permutation
![]() $\upsilon \omega ^{-1} \in S_{n^2}$
. If
$\upsilon \omega ^{-1} \in S_{n^2}$
. If
![]() $\upsilon \omega ^{-1}$
is not the identity, then there exists p with
$\upsilon \omega ^{-1}$
is not the identity, then there exists p with
![]() $\upsilon (\omega ^{-1}(p))> \upsilon (\omega ^{-1}(p+1))$
. Since
$\upsilon (\omega ^{-1}(p))> \upsilon (\omega ^{-1}(p+1))$
. Since
![]() $\upsilon $
and
$\upsilon $
and
![]() $\omega $
are both linear extensions of
$\omega $
are both linear extensions of
![]() $\leq _{\mathsf {NE}}$
, we can have neither
$\leq _{\mathsf {NE}}$
, we can have neither
![]() $\omega ^{-1}(p) \leq _{\mathsf {NE}} \omega ^{-1}(p+1)$
nor
$\omega ^{-1}(p) \leq _{\mathsf {NE}} \omega ^{-1}(p+1)$
nor
![]() $\omega ^{-1}(p+1) \leq _{\mathsf {NE}} \omega ^{-1}(p)$
, so the cells
$\omega ^{-1}(p+1) \leq _{\mathsf {NE}} \omega ^{-1}(p)$
, so the cells
![]() $\omega ^{-1}(p)$
and
$\omega ^{-1}(p)$
and
![]() $\omega ^{-1}(p+1)$
are not in adjacent antidiagonals. Therefore
$\omega ^{-1}(p+1)$
are not in adjacent antidiagonals. Therefore
![]() $\mathsf {word}(D,\omega )$
and
$\mathsf {word}(D,\omega )$
and
![]() $\mathsf {word}(D, s_p \omega )$
are in the same Coxeter commutation class, which by induction also includes
$\mathsf {word}(D, s_p \omega )$
are in the same Coxeter commutation class, which by induction also includes
![]() $\mathsf {word}(D,\upsilon )$
.▪
$\mathsf {word}(D,\upsilon )$
.▪
Each diagonal is an antichain for
![]() $\leq _{\mathsf {NE}}$
, so if
$\leq _{\mathsf {NE}}$
, so if
![]() $\omega $
first lists the elements on diagonal
$\omega $
first lists the elements on diagonal
![]() $-(n-1)$
in any order, then lists the elements on diagonal
$-(n-1)$
in any order, then lists the elements on diagonal
![]() $-(n-2)$
, and so on, then
$-(n-2)$
, and so on, then
![]() $\omega $
is a reading order.
$\omega $
is a reading order.
Definition 3.6 The unimodal-diagonal reading order on
![]() $[n]\times [n]$
is the reading order that lists the elements of the pth diagonal from bottom to top if
$[n]\times [n]$
is the reading order that lists the elements of the pth diagonal from bottom to top if
![]() $p < 0$
, and from top to bottom if
$p < 0$
, and from top to bottom if
![]() $p \geq 0$
. The unimodal-diagonal reading word of
$p \geq 0$
. The unimodal-diagonal reading word of
![]() $D\subseteq [n]\times [n]$
, denoted
$D\subseteq [n]\times [n]$
, denoted
![]() $\mathsf {udiag}(D)$
, is the associated reading word.
$\mathsf {udiag}(D)$
, is the associated reading word.
The unimodal-diagonal reading order on
![]() $\{1,2,3,4\} \times \{1,2,3,4\}$
has values
$\{1,2,3,4\} \times \{1,2,3,4\}$
has values
 $$ \begin{align*} \begin{array}{ccccc} 7 & 6 & 3 & 1 \\ 11 & 8 & 5 & 2 \\ 14 & 12& 9 & 4 \\ 16& 15& 13& 10 \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ccccc} 7 & 6 & 3 & 1 \\ 11 & 8 & 5 & 2 \\ 14 & 12& 9 & 4 \\ 16& 15& 13& 10 \\ \end{array} \end{align*} $$
and if
![]() $D = \{1,2,3,4\} \times \{1,2,3,4\}$
then
$D = \{1,2,3,4\} \times \{1,2,3,4\}$
then
![]() $\mathsf {udiag}(D) = 4536421357246354$
.
$\mathsf {udiag}(D) = 4536421357246354$
.
3.2 Pipe dreams
Recall the definitions of the sets of reduced words
![]() $\mathcal {R}(w)$
, involution words
$\mathcal {R}(w)$
, involution words
![]() $\hat {\mathcal {R}}(y)$
, and fpf-involution words
$\hat {\mathcal {R}}(y)$
, and fpf-involution words
![]() $\hat {\mathcal {R}}^{\mathsf {{FPF}}}(z)$
for
$\hat {\mathcal {R}}^{\mathsf {{FPF}}}(z)$
for
![]() $w \in S_n$
,
$w \in S_n$
,
![]() $y \in \mathcal {I}_n$
, and
$y \in \mathcal {I}_n$
, and
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
from Section 2.1. For the standard reading word, the following theorem is well-known from [Reference Bergeron and Billey1]. The main new results of this section are versions of this theorem for involution pipe dreams and fpf-involution pipe dreams.
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
from Section 2.1. For the standard reading word, the following theorem is well-known from [Reference Bergeron and Billey1]. The main new results of this section are versions of this theorem for involution pipe dreams and fpf-involution pipe dreams.
Theorem 3.7 A subset
![]() $D \subseteq [n]\times [n]$
is a reduced pipe dream for
$D \subseteq [n]\times [n]$
is a reduced pipe dream for
![]() $w \in S_n$
if and only if some (equivalently, every) reading word of D is a reduced word for w.
$w \in S_n$
if and only if some (equivalently, every) reading word of D is a reduced word for w.
Proof Fix
![]() $D \subseteq [n]\times [n]$
and
$D \subseteq [n]\times [n]$
and
![]() $w \in S_n$
. The set
$w \in S_n$
. The set
![]() $\mathcal {R}(w)$
is a union of Coxeter commutation classes, so
$\mathcal {R}(w)$
is a union of Coxeter commutation classes, so
![]() $\mathsf {word}(D)\in \mathcal {R}(w)$
if and only every reading word of D belongs to
$\mathsf {word}(D)\in \mathcal {R}(w)$
if and only every reading word of D belongs to
![]() $\mathcal {R}(w)$
by Lemma 3.5. Saying that D is a reduced pipe dream for w if and only if
$\mathcal {R}(w)$
by Lemma 3.5. Saying that D is a reduced pipe dream for w if and only if
![]() $\mathsf {word}(D) \in \mathcal {R}(w)$
is Bergeron and Billey’s original definition of an rc-graph in [Reference Bergeron and Billey1, Section 3], and it is clear from the basic properties of permutation wiring diagrams that this is equivalent to the definition of a reduced pipe dream in the introduction.▪
$\mathsf {word}(D) \in \mathcal {R}(w)$
is Bergeron and Billey’s original definition of an rc-graph in [Reference Bergeron and Billey1, Section 3], and it is clear from the basic properties of permutation wiring diagrams that this is equivalent to the definition of a reduced pipe dream in the introduction.▪
Corollary 3.8 [Reference Bergeron and Billey1, Lemma 3.2]
If D is a reduced pipe dream for
![]() $w \in S_n$
then
$w \in S_n$
then
![]() $D^T$
is a reduced pipe dream for
$D^T$
is a reduced pipe dream for
![]() $w^{-1}$
.
$w^{-1}$
.
Recall that the set
![]() $\mathcal {ID}(z)$
of involution pipe dreams for
$\mathcal {ID}(z)$
of involution pipe dreams for
![]() $z \in \mathcal {I}_n$
consists of all intersections
$z \in \mathcal {I}_n$
consists of all intersections
![]() where D is a reduced pipe dream for z that is almost-symmetric and
where D is a reduced pipe dream for z that is almost-symmetric and
![]() .
.
Theorem 3.9 Suppose
![]() $z \in \mathcal {I}_n$
and
$z \in \mathcal {I}_n$
and
![]() $D \subseteq [n]\times [n]$
. The following are equivalent:
$D \subseteq [n]\times [n]$
. The following are equivalent:
-
(a) Some reading word of D is an involution word for z.
-
(b) Every reading word of D is an involution word for z.
-
(c) The set D is a reduced pipe dream for some atom of z.
Moreover, if
![]() then
then
![]() $D\in \mathcal {ID}(z)$
if and only if these equivalent conditions hold.
$D\in \mathcal {ID}(z)$
if and only if these equivalent conditions hold.
Remark Although this theorem implies that
![]() $\mathcal {ID}(z) \subseteq \bigsqcup _{w \in \mathcal {A}(z)} \mathcal {PD}(w)$
, it is possible for an atom
$\mathcal {ID}(z) \subseteq \bigsqcup _{w \in \mathcal {A}(z)} \mathcal {PD}(w)$
, it is possible for an atom
![]() $w \in \mathcal {A}(z)$
to have no reduced pipe dreams contained in
$w \in \mathcal {A}(z)$
to have no reduced pipe dreams contained in
![]() , in which case
, in which case
![]() $\mathcal {ID}(z)$
and
$\mathcal {ID}(z)$
and
![]() $\mathcal {PD}(w)$
are disjoint. See Example 3.10 for an illustration of this.
$\mathcal {PD}(w)$
are disjoint. See Example 3.10 for an illustration of this.
Proof Recall that
![]() $\hat {\mathcal {R}}(z)$
is the disjoint union of the sets
$\hat {\mathcal {R}}(z)$
is the disjoint union of the sets
![]() $\mathcal {R}(w)$
, running over all atoms
$\mathcal {R}(w)$
, running over all atoms
![]() $w \in \mathcal {A}(z)$
. The equivalences (a)
$w \in \mathcal {A}(z)$
. The equivalences (a)
![]() $\Leftrightarrow $
(b)
$\Leftrightarrow $
(b)
![]() $\Leftrightarrow $
(c) are clear from Lemma 3.5 and Theorem 3.7. Assume
$\Leftrightarrow $
(c) are clear from Lemma 3.5 and Theorem 3.7. Assume
![]() . To prove the final assertion, it suffices to show that
. To prove the final assertion, it suffices to show that
![]() $D\in \mathcal {ID}(z)$
if and only if the unimodal-diagonal reading word of D from Definition 3.6 is an involution word of z.
$D\in \mathcal {ID}(z)$
if and only if the unimodal-diagonal reading word of D from Definition 3.6 is an involution word of z.
Suppose
![]() $|D| = m$
and
$|D| = m$
and
![]() $\mathsf {udiag}(D) = a_1a_2\cdots a_m$
. We construct a sequence
$\mathsf {udiag}(D) = a_1a_2\cdots a_m$
. We construct a sequence
![]() $w_0,w_1,w_2,\dots ,w_m$
of involutions as follows: start by setting
$w_0,w_1,w_2,\dots ,w_m$
of involutions as follows: start by setting
![]() $w_0 = 1$
, and for each
$w_0 = 1$
, and for each
![]() $i \in [m]$
define
$i \in [m]$
define
![]() $ w_i = s_{a_i} w_{i-1} s_{a_i}$
if we have
$ w_i = s_{a_i} w_{i-1} s_{a_i}$
if we have
![]() $w_{i-1} s_{a_i} \neq s_{a_i} w_{i-1}$
, or else set
$w_{i-1} s_{a_i} \neq s_{a_i} w_{i-1}$
, or else set
![]() $w_i = w_{i-1} s_{a_i} = s_{a_i} w_{i-1}$
. For example, if
$w_i = w_{i-1} s_{a_i} = s_{a_i} w_{i-1}$
. For example, if
![]() $m=5$
and
$m=5$
and
![]() $a_1a_2a_3a_4a_5 =13235$
then this sequence has
$a_1a_2a_3a_4a_5 =13235$
then this sequence has
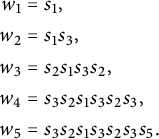 $$ \begin{align*} w_1 &=s_1, \\ w_2&= s_1s_3, \\ w_3 &= s_2s_1s_3s_2, \\ w_4 &= s_3 s_2s_1s_3s_2 s_3, \\ w_5 &=s_3 s_2s_1s_3s_2 s_3 s_5. \end{align*} $$
$$ \begin{align*} w_1 &=s_1, \\ w_2&= s_1s_3, \\ w_3 &= s_2s_1s_3s_2, \\ w_4 &= s_3 s_2s_1s_3s_2 s_3, \\ w_5 &=s_3 s_2s_1s_3s_2 s_3 s_5. \end{align*} $$
Let
![]() $b_l \cdots b_2 b_1$
be the subword of
$b_l \cdots b_2 b_1$
be the subword of
![]() $a_m \cdots a_2 a_1$
which contains
$a_m \cdots a_2 a_1$
which contains
![]() $a_i$
if and only if
$a_i$
if and only if
![]() $w_i = s_{a_i} w_{i-1} s_{a_i}$
. In our example with
$w_i = s_{a_i} w_{i-1} s_{a_i}$
. In our example with
![]() $m=5$
and
$m=5$
and
![]() $a_1a_2a_3a_4a_5= 13235$
, we have
$a_1a_2a_3a_4a_5= 13235$
, we have
![]() $l=2$
and
$l=2$
and
![]() $ b_2 b_1 = a_4a_3= 32$
. Let
$ b_2 b_1 = a_4a_3= 32$
. Let
![]() $(p_1,q_1)$
,
$(p_1,q_1)$
,
![]() $(p_2,q_2)$
, …,
$(p_2,q_2)$
, …,
![]() $(p_m,q_m)$
be the cells in D listed in the unimodal-diagonal reading order and define
$(p_m,q_m)$
be the cells in D listed in the unimodal-diagonal reading order and define
![]() $E = D\sqcup \{ (q_i,p_i) : w_i = s_{a_i} w_{i-1} s_{a_i}\}.$
If
$E = D\sqcup \{ (q_i,p_i) : w_i = s_{a_i} w_{i-1} s_{a_i}\}.$
If
![]() $\mathsf {udiag}(D) = 13235$
then we could have
$\mathsf {udiag}(D) = 13235$
then we could have
By construction
![]() $\mathsf {udiag}(E) = b_l \cdots b_2 b_1 a_1a_2\cdots a_m$
is a reduced word for z. It follows that E is almost-symmetric since each
$\mathsf {udiag}(E) = b_l \cdots b_2 b_1 a_1a_2\cdots a_m$
is a reduced word for z. It follows that E is almost-symmetric since each
![]() $b_i$
has a corresponding
$b_i$
has a corresponding
![]() $a_j$
and the associated cells are transposes of each other.
$a_j$
and the associated cells are transposes of each other.
The exchange principle (see, e.g., [Reference Hultman18, Lemma 3.4]) implies that if
![]() $w \in \mathcal {I}_n$
,
$w \in \mathcal {I}_n$
,
![]() $i \in [n-1]$
, and
$i \in [n-1]$
, and
![]() $w(i)< w(i+1)$
, then either
$w(i)< w(i+1)$
, then either
![]() $s_i ws_i =w\neq ws_i =s_i w = s_i \circ w \circ s_i$
or
$s_i ws_i =w\neq ws_i =s_i w = s_i \circ w \circ s_i$
or
![]() $ s_iw s_i = s_i \circ w \circ s_i \neq w$
. From this, it is straightforward to show that
$ s_iw s_i = s_i \circ w \circ s_i \neq w$
. From this, it is straightforward to show that
![]() $\mathsf {udiag}(D) \in \hat {\mathcal {R}}(z) $
if and only if
$\mathsf {udiag}(D) \in \hat {\mathcal {R}}(z) $
if and only if
![]() $\mathsf {udiag}(E) \in \mathcal {R}(z)$
; this also follows from the results in [Reference Hamaker, Marberg and Pawlowski12, Section 2]. Given the previous paragraph, we conclude that
$\mathsf {udiag}(E) \in \mathcal {R}(z)$
; this also follows from the results in [Reference Hamaker, Marberg and Pawlowski12, Section 2]. Given the previous paragraph, we conclude that
![]() $\mathsf {udiag}(D)\in \mathcal {R}(z)$
if and only if
$\mathsf {udiag}(D)\in \mathcal {R}(z)$
if and only if
![]() is an involution pipe dream for z.▪
is an involution pipe dream for z.▪
Example 3.10 Let
![]() $z = 1432 = \in \mathcal {I}_4$
. Since
$z = 1432 = \in \mathcal {I}_4$
. Since
![]() $ z = s_3 \circ s_2 \circ 1 \circ s_2 \circ s_3 = s_2 \circ s_3 \circ 1 \circ s_3 \circ s_2,$
we have
$ z = s_3 \circ s_2 \circ 1 \circ s_2 \circ s_3 = s_2 \circ s_3 \circ 1 \circ s_3 \circ s_2,$
we have
![]() $ 23 \in \hat {\mathcal {R}}(z)$
and
$ 23 \in \hat {\mathcal {R}}(z)$
and
![]() $ 32\in \hat {\mathcal {R}}(z)$
. These are the standard reading words of the involution pipe dreams
$ 32\in \hat {\mathcal {R}}(z)$
. These are the standard reading words of the involution pipe dreams
![]() $\{(2,1),(3,1)\}$
and
$\{(2,1),(3,1)\}$
and
![]() $\{(2,1),(2,2)\}$
, which may be drawn as
$\{(2,1),(2,2)\}$
, which may be drawn as
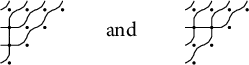
The only involution pipe dream for
![]() $y = 321 \in \mathcal {I}_3$
is
$y = 321 \in \mathcal {I}_3$
is
![]() $\{(1,1),(2,1)\}$
which has standard reading word
$\{(1,1),(2,1)\}$
which has standard reading word
![]() $12$
. Although
$12$
. Although
![]() $\hat {\mathcal {R}}(y) =\{12,21\}$
, there is no involution pipe dream with standard reading word
$\hat {\mathcal {R}}(y) =\{12,21\}$
, there is no involution pipe dream with standard reading word
![]() $21$
.
$21$
.
We turn to the fixed-point-free case.
Lemma 3.11 Assume n is even. Suppose
![]() $z \in \mathcal {I}_n$
is an involution with a symmetric reduced pipe dream
$z \in \mathcal {I}_n$
is an involution with a symmetric reduced pipe dream
![]() $D=D^T$
. Then
$D=D^T$
. Then
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
if and only if
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
if and only if
![]() $\{(i,i) : i \in [n/2]\}\subseteq D$
.
$\{(i,i) : i \in [n/2]\}\subseteq D$
.
Proof In fact, a stronger statement holds: for symmetric D and
![]() $i \in [n/2]$
, the pipes in cell
$i \in [n/2]$
, the pipes in cell
![]() $(i,i)$
of the wiring diagram of D are labeled by fixed points of z if and only if
$(i,i)$
of the wiring diagram of D are labeled by fixed points of z if and only if
![]() $(i,i) \notin D$
. Let a and b be the labels for the pipes entering
$(i,i) \notin D$
. Let a and b be the labels for the pipes entering
![]() $(i,i)$
from the left and below, respectively. Since D is symmetric, if
$(i,i)$
from the left and below, respectively. Since D is symmetric, if
![]() $(i,i) \in D$
then
$(i,i) \in D$
then
![]() $z(a) = b$
(hence
$z(a) = b$
(hence
![]() $z(b) = a$
), and if
$z(b) = a$
), and if
![]() $(i,i) \notin D$
then
$(i,i) \notin D$
then
![]() $z(a) = a$
and
$z(a) = a$
and
![]() $z(b) = b$
.▪
$z(b) = b$
.▪
Recall that the set
![]() $\mathcal {FD}(z)$
of fpf-involution pipe dreams for
$\mathcal {FD}(z)$
of fpf-involution pipe dreams for
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
consists of all intersections
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
consists of all intersections
![]() where D is a reduced pipe dream for z that is symmetric and
where D is a reduced pipe dream for z that is symmetric and
![]() .
.
Theorem 3.12 Suppose n is even,
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
, and
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
, and
![]() $D \subseteq [n]\times [n]$
. The following are equivalent:
$D \subseteq [n]\times [n]$
. The following are equivalent:
-
(a) Some reading word of D is an fpf-involution word for z.
-
(b) Every reading word of D is an fpf-involution word for z.
-
(c) The set D is a reduced pipe dream for some fpf-atom of z.
Moreover, if
![]() then
then
![]() $D\in \mathcal {FD}(z)$
if and only if these equivalent conditions hold.
$D\in \mathcal {FD}(z)$
if and only if these equivalent conditions hold.
Proof Recall that
![]() $\hat {\mathcal {R}}^{\mathsf {{FPF}}}(z)$
is the disjoint union of the sets
$\hat {\mathcal {R}}^{\mathsf {{FPF}}}(z)$
is the disjoint union of the sets
![]() $\mathcal {R}(w)$
, running over all fpf-atoms
$\mathcal {R}(w)$
, running over all fpf-atoms
![]() $w \in \mathcal {A}^{\mathsf {{FPF}}}(z)$
. Properties (a), (b), and (c) are again equivalent by Lemma 3.5 and Theorem 3.7. Assume
$w \in \mathcal {A}^{\mathsf {{FPF}}}(z)$
. Properties (a), (b), and (c) are again equivalent by Lemma 3.5 and Theorem 3.7. Assume
![]() . To prove the final assertion, it suffices to check that D is an fpf-involution pipe dream for z if and only if
. To prove the final assertion, it suffices to check that D is an fpf-involution pipe dream for z if and only if
![]() $\mathsf {udiag}(D) \in \hat {\mathcal {R}}^{\mathsf {{FPF}}}(z)$
.
$\mathsf {udiag}(D) \in \hat {\mathcal {R}}^{\mathsf {{FPF}}}(z)$
.
To this end, first suppose
![]() where
where
![]() $E=E^T \in \mathcal {PD}(z)$
. Then E is also almost-symmetric, so Theorem 3.9 implies that
$E=E^T \in \mathcal {PD}(z)$
. Then E is also almost-symmetric, so Theorem 3.9 implies that
![]() . This combined with Lemma 3.11 implies that
. This combined with Lemma 3.11 implies that
![]() , so
, so
![]() $\mathsf {udiag}(D) \in \hat {\mathcal {R}}^{\mathsf {{FPF}}}(z)$
.
$\mathsf {udiag}(D) \in \hat {\mathcal {R}}^{\mathsf {{FPF}}}(z)$
.
Conversely, suppose every reading word of D is an fpf-involution word for z, so that
![]() $\mathsf {udiag}(D) \in \hat {\mathcal {R}}^{\mathsf {{FPF}}}(z)$
. The set
$\mathsf {udiag}(D) \in \hat {\mathcal {R}}^{\mathsf {{FPF}}}(z)$
. The set
![]() $D' = D \sqcup \{(i,i) : i \in [n-1]\}$
then has
$D' = D \sqcup \{(i,i) : i \in [n-1]\}$
then has
![]() $\mathsf {udiag}(D') \in \hat {\mathcal {R}}(z)$
, so there exists an almost-symmetric
$\mathsf {udiag}(D') \in \hat {\mathcal {R}}(z)$
, so there exists an almost-symmetric
![]() $D'' \in \mathcal {PD}(z)$
with
$D'' \in \mathcal {PD}(z)$
with
![]() by Theorem 3.9. By construction
by Theorem 3.9. By construction
![]() , and since
, and since
![]() $|D''| = \ell (z) = 2|D| + n/2$
it follows that
$|D''| = \ell (z) = 2|D| + n/2$
it follows that
![]() $D''$
is actually symmetric. Therefore,
$D''$
is actually symmetric. Therefore,
![]() $D\in \mathcal {FD}(z)$
.▪
$D\in \mathcal {FD}(z)$
.▪
Example 3.13 Let
![]() $z =216543 \in \mathcal {I}^{\mathsf {{FPF}}}_6$
. Then
$z =216543 \in \mathcal {I}^{\mathsf {{FPF}}}_6$
. Then
![]() $\ell (z) = 7$
and
$\ell (z) = 7$
and
so
![]() $3413543$
and
$3413543$
and
![]() $5413545$
are reduced words for z. These words are the unimodal-diagonal reading words of the symmetric reduced pipe dreams
$5413545$
are reduced words for z. These words are the unimodal-diagonal reading words of the symmetric reduced pipe dreams

so
![]() $\{(3,1),(3,2)\}$
and
$\{(3,1),(3,2)\}$
and
![]() $\{(4,1),(5,1)\}$
are fpf-involution pipe dreams for z, and their standard reading words
$\{(4,1),(5,1)\}$
are fpf-involution pipe dreams for z, and their standard reading words
![]() $43$
and
$43$
and
![]() $45$
are fpf-involution words for z.
$45$
are fpf-involution words for z.
4 Pipe dreams and Schubert polynomials
In this section, we derive the pipe dream formulas for involution Schubert polynomials given in Theorem 1.5. Our arguments are inspired by a new proof due to Knutson [Reference Knutson22] of the classical pipe dream formula (1.2). Knutson’s approach is inductive. The key step in his argument is to show that the right side of (1.2) satisfies certain recurrences that also apply to double Schubert polynomials [Reference Kohnert and Veigneau25, Section 4].
Similar recurrences for
![]() $\hat {\mathfrak {S}}_y$
and
$\hat {\mathfrak {S}}_y$
and
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
appear in [Reference Hamaker, Marberg and Pawlowski14]. Adapting Knutson’s strategy to our setting requires us to show that the right hand expressions in Theorem 1.5 satisfy the same family of identities. This is accomplished in Theorems 4.23 and 4.34. Proving these results involves a detailed analysis of the maximal (shifted) Ferrers diagram contained in a reduced pipe dream, which we refer to as the (shifted) dominant component. We gradually develop the technical properties of these components over the course of this section.
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
appear in [Reference Hamaker, Marberg and Pawlowski14]. Adapting Knutson’s strategy to our setting requires us to show that the right hand expressions in Theorem 1.5 satisfy the same family of identities. This is accomplished in Theorems 4.23 and 4.34. Proving these results involves a detailed analysis of the maximal (shifted) Ferrers diagram contained in a reduced pipe dream, which we refer to as the (shifted) dominant component. We gradually develop the technical properties of these components over the course of this section.
4.1 Dominant components of permutations
The results in this subsection are all straightforward consequences of known results, with the possible exception of Lemma 4.2; see in particular [Reference Knutson22, Section 3]. However, we are unaware of an explicit description of Definition 4.1 in the literature. Since this definition is central to our construction, we give a self-contained treatment of its properties.
A lower set in a poset
![]() $(P,<)$
is a subset
$(P,<)$
is a subset
![]() $L \subset P$
such that if
$L \subset P$
such that if
![]() $x \in P$
,
$x \in P$
,
![]() $y \in L$
, and
$y \in L$
, and
![]() $x < y$
, then
$x < y$
, then
![]() $x \in L$
. Let
$x \in L$
. Let
![]() $\leq _{\mathsf {NW}}$
be the partial order on
$\leq _{\mathsf {NW}}$
be the partial order on
![]() $\mathbb {Z}_{>0} \times \mathbb {Z}_{>0}$
with
$\mathbb {Z}_{>0} \times \mathbb {Z}_{>0}$
with
![]() $(i,j) \leq _{\mathsf {NW}} (i',j')$
if
$(i,j) \leq _{\mathsf {NW}} (i',j')$
if
![]() $i \leq i'$
and
$i \leq i'$
and
![]() $j \leq j'$
, i.e., if
$j \leq j'$
, i.e., if
![]() $(i,j)$
is northwest of
$(i,j)$
is northwest of
![]() $(i',j')$
in matrix coordinates.
$(i',j')$
in matrix coordinates.
Definition 4.1 The dominant component
![]() $\operatorname {dom}(D)$
of a set
$\operatorname {dom}(D)$
of a set
![]() $D \subseteq \mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
is the maximal lower set in
$D \subseteq \mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
is the maximal lower set in
![]() $(\mathbb {Z}_{>0}\times \mathbb {Z}_{>0},\leq _{\mathsf {NW}})$
contained in D.
$(\mathbb {Z}_{>0}\times \mathbb {Z}_{>0},\leq _{\mathsf {NW}})$
contained in D.
Equivalently, the set
![]() $\operatorname {dom}(D)$
consists of all
$\operatorname {dom}(D)$
consists of all
![]() $(i,j) \in D$
such that if
$(i,j) \in D$
such that if
![]() $(i',j') \in \mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
and
$(i',j') \in \mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
and
![]() $(i',j') \leq _{\mathsf {NW}} (i,j)$
then
$(i',j') \leq _{\mathsf {NW}} (i,j)$
then
![]() $(i',j') \in D$
. If D is finite, then its dominant component
$(i',j') \in D$
. If D is finite, then its dominant component
![]() $\operatorname {dom}(D)$
is the Ferrers diagram
$\operatorname {dom}(D)$
is the Ferrers diagram
![]() $ \mathsf {D}_\lambda = \{(i,j) : 1 \leq i \leq \ell (\lambda ),\ 1 \leq j \leq \lambda _i\} $
of some partition
$ \mathsf {D}_\lambda = \{(i,j) : 1 \leq i \leq \ell (\lambda ),\ 1 \leq j \leq \lambda _i\} $
of some partition
![]() $\lambda $
. An outer corner of D is a pair
$\lambda $
. An outer corner of D is a pair
![]() $(i,j) \in (\mathbb {Z}_{>0} \times \mathbb {Z}_{>0}) \setminus D$
such that
$(i,j) \in (\mathbb {Z}_{>0} \times \mathbb {Z}_{>0}) \setminus D$
such that
![]() $\operatorname {dom}(D) \sqcup \{(i,j)\}$
is again a Ferrers diagram of some partition. For example,
$\operatorname {dom}(D) \sqcup \{(i,j)\}$
is again a Ferrers diagram of some partition. For example,
![]() $(1,2)$
and
$(1,2)$
and
![]() $(2,1)$
are the outer corners of
$(2,1)$
are the outer corners of
![]() $D = \{(1,1),(1,3)\}$
, since
$D = \{(1,1),(1,3)\}$
, since
![]() $\operatorname {dom}(D) = \{(1,1)\}$
.
$\operatorname {dom}(D) = \{(1,1)\}$
.
For distinct
![]() $i,j \in [n]$
, let
$i,j \in [n]$
, let
![]() $t_{ij} \in S_n$
be the transposition interchanging i and j.
$t_{ij} \in S_n$
be the transposition interchanging i and j.
Lemma 4.2 Suppose
![]() $w \in S_n$
and
$w \in S_n$
and
![]() $(i,j)$
is an outer corner of some
$(i,j)$
is an outer corner of some
![]() $D \in \mathcal {PD}(w)$
. Then
$D \in \mathcal {PD}(w)$
. Then
![]() $w(i) = j$
and
$w(i) = j$
and
![]() $D\sqcup \{(i,j)\}$
is a reduced pipe dream (for a longer permutation).
$D\sqcup \{(i,j)\}$
is a reduced pipe dream (for a longer permutation).
Proof By hypothesis, D contains every cell above
![]() $(i,j)$
in the jth column and every cell to the left of
$(i,j)$
in the jth column and every cell to the left of
![]() $(i,j)$
in the ith row. This means that in the wiring diagram associated to D, the pipe leaving the top of position
$(i,j)$
in the ith row. This means that in the wiring diagram associated to D, the pipe leaving the top of position
![]() $(i,j)$
must continue straight up and terminate in column j on the top side of D, and after leaving the left of position
$(i,j)$
must continue straight up and terminate in column j on the top side of D, and after leaving the left of position
![]() $(i,j)$
, the same pipe must continue straight left and terminate in row i on the left side of D. Thus
$(i,j)$
, the same pipe must continue straight left and terminate in row i on the left side of D. Thus
![]() $w(i) = j$
as claimed. Suppose the other pipe at position
$w(i) = j$
as claimed. Suppose the other pipe at position
![]() $(i,j)$
starts at p on the left and ends at
$(i,j)$
starts at p on the left and ends at
![]() $q=w(p)$
on the top. As this pipe leaves
$q=w(p)$
on the top. As this pipe leaves
![]() $(i,j)$
rightwards and downwards, we have
$(i,j)$
rightwards and downwards, we have
![]() $p> i$
and
$p> i$
and
![]() $q>j$
, and the pipe only intersects
$q>j$
, and the pipe only intersects
![]() $[i] \times [j]$
at
$[i] \times [j]$
at
![]() $(i,j)$
, where it avoids the other pipe. Therefore, we have
$(i,j)$
, where it avoids the other pipe. Therefore, we have
![]() $D\sqcup \{(i,j)\} \in \mathcal {PD}(w')$
for
$D\sqcup \{(i,j)\} \in \mathcal {PD}(w')$
for
![]() $w' :=wt_{ip} = t_{jq}w\in S_n$
, and it holds that
$w' :=wt_{ip} = t_{jq}w\in S_n$
, and it holds that
![]() $\ell (w) < \ell (w')$
as
$\ell (w) < \ell (w')$
as
![]() $i< p$
and
$i< p$
and
![]() $w(i)< w(p)$
.▪
$w(i)< w(p)$
.▪
Example 4.3 Suppose
![]() $w=426135 \in S_6$
. If
$w=426135 \in S_6$
. If
![]() $(i,j) = (2,2)$
and
$(i,j) = (2,2)$
and
then in the notation of the proof, we have
![]() $p = 3$
,
$p = 3$
,
![]() $q=6$
, and
$q=6$
, and
![]() $w' = 462135$
.
$w' = 462135$
.
The Rothe diagram of
![]() $w \in S_n$
is
$w \in S_n$
is
It is often useful to observe that the set
![]() $D(w)$
is the complement in
$D(w)$
is the complement in
![]() $[n]\times [n]$
of the union of the hooks
$[n]\times [n]$
of the union of the hooks
![]() $\{ (x,w(i)) : i < x \leq n\} \sqcup \{ (i,w(i))\} \sqcup \{ (i,y) : w(i) < y \leq n\}$
for
$\{ (x,w(i)) : i < x \leq n\} \sqcup \{ (i,w(i))\} \sqcup \{ (i,y) : w(i) < y \leq n\}$
for
![]() $i \in [n]$
. It is not hard to show that one always has
$i \in [n]$
. It is not hard to show that one always has
![]() $|D(w)| = \ell (w)$
.
$|D(w)| = \ell (w)$
.
Definition 4.4 The dominant component of a permutation
![]() $w \in S_n$
is
$w \in S_n$
is
![]() $\operatorname {dom}(w) = \operatorname {dom}(D(w)).$
We say that permutation
$\operatorname {dom}(w) = \operatorname {dom}(D(w)).$
We say that permutation
![]() $w \in S_n$
is dominant if
$w \in S_n$
is dominant if
![]() $\operatorname {dom}(w) \in \mathcal {PD}(w)$
.
$\operatorname {dom}(w) \in \mathcal {PD}(w)$
.
It is more common to define w to be dominant if
![]() $D(w)$
is the Ferrers diagram of a partition, or equivalently if w is
$D(w)$
is the Ferrers diagram of a partition, or equivalently if w is
![]() $132$
-avoiding. The following lemma shows that our definition is equivalent.
$132$
-avoiding. The following lemma shows that our definition is equivalent.
Lemma 4.5 A permutation
![]() $w \in S_n$
is dominant if and only if it holds that
$w \in S_n$
is dominant if and only if it holds that
![]() $\mathcal {PD}(w) = \{ \operatorname {dom}(w)\}$
, in which case
$\mathcal {PD}(w) = \{ \operatorname {dom}(w)\}$
, in which case
![]() $\operatorname {dom}(w) = D(w)$
.
$\operatorname {dom}(w) = D(w)$
.
Proof If
![]() $w \in S_n$
is dominant then
$w \in S_n$
is dominant then
![]() $\mathcal {PD}(w) = \{ \operatorname {dom}(w)\}= \{ D(w) \}$
since all reduced pipe dreams for w have size
$\mathcal {PD}(w) = \{ \operatorname {dom}(w)\}= \{ D(w) \}$
since all reduced pipe dreams for w have size
![]() $\ell (w) = |D(w)|$
and contain
$\ell (w) = |D(w)|$
and contain
![]() $\operatorname {dom}(w) \subseteq D(w)$
.▪
$\operatorname {dom}(w) \subseteq D(w)$
.▪
Corollary 4.6 Let
![]() $w \in S_n$
. Then
$w \in S_n$
. Then
![]() $\operatorname {dom}(w^{-1}) = \operatorname {dom}(w)^T$
. If
$\operatorname {dom}(w^{-1}) = \operatorname {dom}(w)^T$
. If
![]() $w $
is dominant, then
$w $
is dominant, then
![]() $\operatorname {dom}(w) = \operatorname {dom}(w)^T$
if and only if
$\operatorname {dom}(w) = \operatorname {dom}(w)^T$
if and only if
![]() $w=w^{-1}$
.
$w=w^{-1}$
.
Proof The first claim holds since
![]() $D(w^{-1}) = D(w)^T$
. If w is dominant and
$D(w^{-1}) = D(w)^T$
. If w is dominant and
![]() $\operatorname {dom}(w) = \operatorname {dom}(w)^T$
, then
$\operatorname {dom}(w) = \operatorname {dom}(w)^T$
, then
![]() $\operatorname {dom}(w) = D(w)$
by Lemma 4.5 so
$\operatorname {dom}(w) = D(w)$
by Lemma 4.5 so
![]() $D(w) = D(w)^T = D(w^{-1})$
and therefore
$D(w) = D(w)^T = D(w^{-1})$
and therefore
![]() $w=w^{-1}$
.▪
$w=w^{-1}$
.▪
We write
![]() $\mu \subseteq \lambda $
for partitions
$\mu \subseteq \lambda $
for partitions
![]() $\mu $
and
$\mu $
and
![]() $\lambda $
to indicate that
$\lambda $
to indicate that
![]() $\mathsf {D}_\mu \subseteq \mathsf {D}_\lambda $
.
$\mathsf {D}_\mu \subseteq \mathsf {D}_\lambda $
.
Proposition 4.7 If
![]() $\lambda $
is a partition with
$\lambda $
is a partition with
![]() $\lambda \subseteq (n-1,\dots ,3, 2,1)$
then there exists a unique dominant permutation
$\lambda \subseteq (n-1,\dots ,3, 2,1)$
then there exists a unique dominant permutation
![]() $w \in S_n$
with
$w \in S_n$
with
![]() $\operatorname {dom}(w) = \mathsf {D}_\lambda $
.
$\operatorname {dom}(w) = \mathsf {D}_\lambda $
.
Proof This holds by induction as adding an outer corner to the reduced pipe dream of a dominant permutation yields a reduced pipe dream of a dominant permutation.▪
Write
![]() $\leq $
for the Bruhat order on
$\leq $
for the Bruhat order on
![]() $S_n$
. Since
$S_n$
. Since
![]() $v \leq w$
if and only if some (equivalently, every) reduced word for w has a subword that is a reduced word for v [Reference Humphreys20, Section 5.10], Theorem 3.7 implies:
$v \leq w$
if and only if some (equivalently, every) reduced word for w has a subword that is a reduced word for v [Reference Humphreys20, Section 5.10], Theorem 3.7 implies:
Lemma 4.8 If
![]() $v,w \in S_n$
then
$v,w \in S_n$
then
![]() $v \leq w$
if and only if some (equivalently, every) reduced pipe dream for w has a subset that is a reduced pipe dream for v.
$v \leq w$
if and only if some (equivalently, every) reduced pipe dream for w has a subset that is a reduced pipe dream for v.
Corollary 4.9 Let
![]() $v,w \in S_n$
with v dominant. Then
$v,w \in S_n$
with v dominant. Then
![]() $v\leq w$
if and only if
$v\leq w$
if and only if
![]() $\operatorname {dom}(v) \subseteq D$
for some (equivalently, every)
$\operatorname {dom}(v) \subseteq D$
for some (equivalently, every)
![]() $D \in \mathcal {PD}(w)$
.
$D \in \mathcal {PD}(w)$
.
Proof This holds since a dominant permutation has only one reduced pipe dream.▪
For each
![]() $i \in [n]$
let
$i \in [n]$
let
![]() $c_i(w) = |\{ j : (i,j) \in D(w)\}|.$
The code of
$c_i(w) = |\{ j : (i,j) \in D(w)\}|.$
The code of
![]() $w \in S_n$
is the integer sequence
$w \in S_n$
is the integer sequence
![]() $ c(w) = (c_1(w), \ldots , c_n(w))$
. The bottom pipe dream of
$ c(w) = (c_1(w), \ldots , c_n(w))$
. The bottom pipe dream of
![]() $w \in S_n$
is the set
$w \in S_n$
is the set
obtained by left-justifying
![]() $D(w)$
. It is not obvious that
$D(w)$
. It is not obvious that
![]() $D_{\text {bot}}(w) \in \mathcal {PD}(w)$
, but this holds by results in [Reference Bergeron and Billey1]; see also Theorem 5.2 below.
$D_{\text {bot}}(w) \in \mathcal {PD}(w)$
, but this holds by results in [Reference Bergeron and Billey1]; see also Theorem 5.2 below.
Example 4.10 If
![]() $w = 35142 \in S_5$
, then
$w = 35142 \in S_5$
, then
![]() $D(w)$
is the set of
$D(w)$
is the set of
![]() $+$
’s below:
$+$
’s below:
 $$ \begin{align*} \begin{array}{ccccc} + & + & 1 & \cdot & \cdot\\ + & + & \cdot & + & 1\\ 1 & \cdot & \cdot & \cdot & \cdot\\ \cdot & + & \cdot & 1 & \cdot\\ \cdot & 1 & \cdot & \cdot & \cdot \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{ccccc} + & + & 1 & \cdot & \cdot\\ + & + & \cdot & + & 1\\ 1 & \cdot & \cdot & \cdot & \cdot\\ \cdot & + & \cdot & 1 & \cdot\\ \cdot & 1 & \cdot & \cdot & \cdot \end{array} \end{align*} $$
so we have
![]() $c(w) = (2,3,0,1,0)$
and
$c(w) = (2,3,0,1,0)$
and
 $$ \begin{align*} D_{\text{bot}}(w) = \begin{array}{ccccc} + & + & \cdot & \,\cdot\\ + & + & + & \,\cdot\\ \cdot & \cdot & \cdot & \,\cdot \\ + & \cdot & \cdot & \,\cdot \\ \cdot & \cdot & \cdot & \,\cdot \end{array} \end{align*} $$
$$ \begin{align*} D_{\text{bot}}(w) = \begin{array}{ccccc} + & + & \cdot & \,\cdot\\ + & + & + & \,\cdot\\ \cdot & \cdot & \cdot & \,\cdot \\ + & \cdot & \cdot & \,\cdot \\ \cdot & \cdot & \cdot & \,\cdot \end{array} \end{align*} $$
Proposition 4.11 If
![]() $w \in S_n$
and
$w \in S_n$
and
![]() $D \in \mathcal {PD}(w)$
then
$D \in \mathcal {PD}(w)$
then
![]() $\operatorname {dom}(D) = \operatorname {dom}(w)$
.
$\operatorname {dom}(D) = \operatorname {dom}(w)$
.
Proof For each
![]() $D \in \mathcal {PD}(w)$
there exists a dominant permutation
$D \in \mathcal {PD}(w)$
there exists a dominant permutation
![]() $v \in S_n$
with
$v \in S_n$
with
![]() $\operatorname {dom}(v) = \operatorname {dom}(D)$
and
$\operatorname {dom}(v) = \operatorname {dom}(D)$
and
![]() $v \leq w$
, in which case
$v \leq w$
, in which case
![]() $\operatorname {dom}(D) \subseteq \operatorname {dom}(E)$
for all
$\operatorname {dom}(D) \subseteq \operatorname {dom}(E)$
for all
![]() $E \in \mathcal {PD}(w)$
by Corollary 4.9. This can only hold if
$E \in \mathcal {PD}(w)$
by Corollary 4.9. This can only hold if
![]() $\operatorname {dom}(D) = \operatorname {dom}(E)$
for all
$\operatorname {dom}(D) = \operatorname {dom}(E)$
for all
![]() $E \in \mathcal {PD}(w)$
.
$E \in \mathcal {PD}(w)$
.
To finish the proof, it suffices to show that
![]() $\operatorname {dom}(w) = \operatorname {dom}(D_{\text {bot}}(w))$
. It is clear by definition that
$\operatorname {dom}(w) = \operatorname {dom}(D_{\text {bot}}(w))$
. It is clear by definition that
![]() $\operatorname {dom}(w) \subseteq \operatorname {dom}(D_{\text {bot}}(w))$
. Conversely, each outer corner of
$\operatorname {dom}(w) \subseteq \operatorname {dom}(D_{\text {bot}}(w))$
. Conversely, each outer corner of
![]() $\operatorname {dom}(w)$
has the form
$\operatorname {dom}(w)$
has the form
![]() $(i,w(i))$
for some
$(i,w(i))$
for some
![]() $i \in [n]$
but no such cell is in
$i \in [n]$
but no such cell is in
![]() $\operatorname {dom}(D_{\text {bot}}(w))$
, so we cannot have
$\operatorname {dom}(D_{\text {bot}}(w))$
, so we cannot have
![]() $\operatorname {dom}(w) \subsetneq \operatorname {dom}(D_{\text {bot}}(w))$
.▪
$\operatorname {dom}(w) \subsetneq \operatorname {dom}(D_{\text {bot}}(w))$
.▪
Below, we define an outer corner of
![]() $w \in S_n$
to be an outer corner of
$w \in S_n$
to be an outer corner of
![]() $\operatorname {dom}(w)$
.
$\operatorname {dom}(w)$
.
4.2 Involution pipe dream formulas
Recall that
![]() $\mathcal {I}_n = \{ w \in S_n : w=w^{-1}\}$
and
$\mathcal {I}_n = \{ w \in S_n : w=w^{-1}\}$
and
![]() .
.
Definition 4.12 The shifted dominant component of
![]() $z \in \mathcal {I}_n$
is the set
$z \in \mathcal {I}_n$
is the set
![]()
Fix
![]() $z \in \mathcal {I}_n$
. By Proposition 4.11,
$z \in \mathcal {I}_n$
. By Proposition 4.11,
![]() for all
for all
![]() $D \in \mathcal {PD}(z)$
. The shifted Ferrers diagram of a strict partition
$D \in \mathcal {PD}(z)$
. The shifted Ferrers diagram of a strict partition
![]() $\lambda = (\lambda _1>\lambda _2 > \dots > \lambda _k >0)$
is the set
$\lambda = (\lambda _1>\lambda _2 > \dots > \lambda _k >0)$
is the set
which is formed from
![]() $\mathsf {D}_\lambda $
by moving the boxes in row i to the right by
$\mathsf {D}_\lambda $
by moving the boxes in row i to the right by
![]() $i-1$
columns. Since
$i-1$
columns. Since
![]() $\operatorname {dom}(z)$
is a Ferrers diagram, the set
$\operatorname {dom}(z)$
is a Ferrers diagram, the set
![]() $\operatorname {shdom}(z)$
is the transpose of the shifted Ferrers diagram of some strict partition. A pair
$\operatorname {shdom}(z)$
is the transpose of the shifted Ferrers diagram of some strict partition. A pair
![]() $(j,i) \in \mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
with
$(j,i) \in \mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
with
![]() $i\leq j$
is an outer corner of z if and only if the transpose of
$i\leq j$
is an outer corner of z if and only if the transpose of
![]() $\operatorname {shdom}(z) \cup \{(j,i)\}$
is a shifted Ferrers diagram, in which case
$\operatorname {shdom}(z) \cup \{(j,i)\}$
is a shifted Ferrers diagram, in which case
![]() $z(j) = i$
.
$z(j) = i$
.
Lemma 4.13 If
![]() $z \in \mathcal {I}_n$
then
$z \in \mathcal {I}_n$
then
![]() $\operatorname {dom}(z) = \operatorname {shdom}(z) \cup \operatorname {shdom}(z)^T$
.
$\operatorname {dom}(z) = \operatorname {shdom}(z) \cup \operatorname {shdom}(z)^T$
.
Proof This holds since
![]() $z=z^{-1}$
implies that
$z=z^{-1}$
implies that
![]() $\operatorname {dom}(z) = \operatorname {dom}(z)^T$
.▪
$\operatorname {dom}(z) = \operatorname {dom}(z)^T$
.▪
Corollary 4.14 If
![]() $z \in \mathcal {I}_n$
then
$z \in \mathcal {I}_n$
then
![]() $\operatorname {shdom}(z)$
is the union of all lower sets of
$\operatorname {shdom}(z)$
is the union of all lower sets of
![]() that are contained in some (equivalently, every)
that are contained in some (equivalently, every)
![]() $D \in \mathcal {ID}(z)$
.
$D \in \mathcal {ID}(z)$
.
The natural definition of “involution” dominance turns out to be equivalent to the usual notion:
Proposition 4.15 Let
![]() $z \in \mathcal {I}_n$
. The following are equivalent:
$z \in \mathcal {I}_n$
. The following are equivalent:
-
(a) The permutation z is dominant.
-
(b) It holds that
 $\mathcal {PD}(z) = \{ \operatorname {dom}(z)\}$
.
$\mathcal {PD}(z) = \{ \operatorname {dom}(z)\}$
. -
(c) It holds that
 $\mathcal {ID}(z) = \{\operatorname {shdom}(z)\}$
.
$\mathcal {ID}(z) = \{\operatorname {shdom}(z)\}$
.
Proof We have (a)
![]() $\Leftrightarrow $
(b) by Lemma 4.5 and (b)
$\Leftrightarrow $
(b) by Lemma 4.5 and (b)
![]() $\Leftrightarrow $
(c) by Lemma 4.13.▪
$\Leftrightarrow $
(c) by Lemma 4.13.▪
Proposition 4.16 If
![]() $\lambda $
is a strict partition with
$\lambda $
is a strict partition with
![]() $\lambda \subseteq (n-1,n-3,n-5,\dots )$
then there exists a unique dominant involution
$\lambda \subseteq (n-1,n-3,n-5,\dots )$
then there exists a unique dominant involution
![]() $z \in \mathcal {I}_n$
with
$z \in \mathcal {I}_n$
with
![]() $\operatorname {shdom}(z)^T = \mathsf {SD}_\lambda $
.
$\operatorname {shdom}(z)^T = \mathsf {SD}_\lambda $
.
Proof We have
![]() $\mathsf {D}_\mu = \mathsf {SD}_\lambda \cup ( \mathsf {SD}_\lambda )^T$
for some
$\mathsf {D}_\mu = \mathsf {SD}_\lambda \cup ( \mathsf {SD}_\lambda )^T$
for some
![]() $\mu $
. Let
$\mu $
. Let
![]() $z \in S_n$
be dominant with
$z \in S_n$
be dominant with
![]() $\operatorname {dom}(z) = \mathsf {D}_\mu $
. Then
$\operatorname {dom}(z) = \mathsf {D}_\mu $
. Then
![]() $z \in \mathcal {I}_n$
by Corollary 4.6 and
$z \in \mathcal {I}_n$
by Corollary 4.6 and
![]() . Uniqueness holds by Lemma 4.13.▪
. Uniqueness holds by Lemma 4.13.▪
If
![]() $y,z \in \mathcal {I}_n$
, then
$y,z \in \mathcal {I}_n$
, then
![]() $y \leq z$
in Bruhat order if and only if some (equivalently, every) involution word for z contains a subword that is an involution word for y (see either [Reference Richardson and Springer40, Corollary 8.10] with [Reference Richardson and Springer41], or [Reference Hultman19, Theorem 2.8]). The following is an immediate corollary of this property and Theorem 3.9.
$y \leq z$
in Bruhat order if and only if some (equivalently, every) involution word for z contains a subword that is an involution word for y (see either [Reference Richardson and Springer40, Corollary 8.10] with [Reference Richardson and Springer41], or [Reference Hultman19, Theorem 2.8]). The following is an immediate corollary of this property and Theorem 3.9.
Lemma 4.17 Let
![]() $y,z \in \mathcal {I}_n$
. Then
$y,z \in \mathcal {I}_n$
. Then
![]() $y \leq z$
if and only if some (equivalently, every) involution pipe dream for z has a subset that is an involution pipe dream for y.
$y \leq z$
if and only if some (equivalently, every) involution pipe dream for z has a subset that is an involution pipe dream for y.
Corollary 4.18 Let
![]() $y,z \in \mathcal {I}_n$
with y dominant. Then
$y,z \in \mathcal {I}_n$
with y dominant. Then
![]() $y\leq z$
if and only if
$y\leq z$
if and only if
![]() $\operatorname {shdom}(y) \subseteq D$
for some (equivalently, every)
$\operatorname {shdom}(y) \subseteq D$
for some (equivalently, every)
![]() $D \in \mathcal {ID}(z)$
.
$D \in \mathcal {ID}(z)$
.
Proof This is clear since if
![]() $y \in \mathcal {I}_n$
is dominant then
$y \in \mathcal {I}_n$
is dominant then
![]() $|\mathcal {ID}(y)|=1$
.▪
$|\mathcal {ID}(y)|=1$
.▪
We will need the following technical property of the Demazure product from [Reference Knutson and Miller24].
Lemma 4.19 [Reference Knutson and Miller24, Lemma 3.4(1)]
If
![]() $b_1b_2\cdots b_q$
is a subword of
$b_1b_2\cdots b_q$
is a subword of
![]() $a_1a_2\cdots a_p$
where each
$a_1a_2\cdots a_p$
where each
![]() $a_i \in [n-1]$
, then
$a_i \in [n-1]$
, then
![]() $ s_{b_1} \circ s_{b_2}\circ \dots \circ s_{b_q} \leq s_{a_1} \circ s_{a_2}\circ \dots \circ s_{a_p} \in S_n. $
$ s_{b_1} \circ s_{b_2}\circ \dots \circ s_{b_q} \leq s_{a_1} \circ s_{a_2}\circ \dots \circ s_{a_p} \in S_n. $
Corollary 4.20 If
![]() $v',w',v,w \in S_n$
, and
$v',w',v,w \in S_n$
, and
![]() $v \leq w$
, and
$v \leq w$
, and
![]() $v'\leq w'$
then
$v'\leq w'$
then
![]() $v' \circ v \leq w' \circ w$
.
$v' \circ v \leq w' \circ w$
.
Proof This is clear from Lemma 4.19 given the subword property of
![]() $\leq $
.▪
$\leq $
.▪
Corollary 4.21 If
![]() $v,w \in S_n$
and
$v,w \in S_n$
and
![]() $v \leq w$
then
$v \leq w$
then
![]() $v^{-1}\circ v \leq w^{-1} \circ w$
.
$v^{-1}\circ v \leq w^{-1} \circ w$
.
Proof Apply Corollary 4.20 with
![]() $v' = v^{-1}$
and
$v' = v^{-1}$
and
![]() $w'=w^{-1}$
.▪
$w'=w^{-1}$
.▪
Recall
![]() $t_{ij} \in S_n$
is a transposition for distinct
$t_{ij} \in S_n$
is a transposition for distinct
![]() $i,j \in [n]$
. It is well-known and not hard to check that if
$i,j \in [n]$
. It is well-known and not hard to check that if
![]() $w \in S_n$
then
$w \in S_n$
then
![]() $\ell (w t_{ij}) = \ell (w) +1$
if and only if
$\ell (w t_{ij}) = \ell (w) +1$
if and only if
![]() $w(i)< w(j)$
and no
$w(i)< w(j)$
and no
![]() $i< e< j$
has
$i< e< j$
has
![]() $w(i) < w(e) < w(j)$
.
$w(i) < w(e) < w(j)$
.
Given
![]() $y \in \mathcal {I}_n$
and
$y \in \mathcal {I}_n$
and
![]() $1\leq i < j \leq n$
, let
$1\leq i < j \leq n$
, let
![]() $\mathcal {A}_{ij}(y)= \{ w t_{ij} : w \in \mathcal {A}(y)\text {, }\ell (wt_{ij})=\ell (w)+1\}.$
Each covering relation in
$\mathcal {A}_{ij}(y)= \{ w t_{ij} : w \in \mathcal {A}(y)\text {, }\ell (wt_{ij})=\ell (w)+1\}.$
Each covering relation in
![]() $(S_n,\leq )$
arises as the image of right multiplication by some transposition
$(S_n,\leq )$
arises as the image of right multiplication by some transposition
![]() $t_{ij}$
. The following theorem characterizes certain operators
$t_{ij}$
. The following theorem characterizes certain operators
![]() $\tau _{ij}$
which play an analogous role for
$\tau _{ij}$
which play an analogous role for
![]() $(\mathcal {I}_n,\leq )$
.
$(\mathcal {I}_n,\leq )$
.
Theorem 4.22 (See [Reference Hamaker, Marberg and Pawlowski14, Section 3])
For each pair of integers
![]() $1\leq i < j \leq n$
, there are unique maps
$1\leq i < j \leq n$
, there are unique maps
![]() $\tau _{ij} : \mathcal {I}_n \to \mathcal {I}_n$
with the following properties:
$\tau _{ij} : \mathcal {I}_n \to \mathcal {I}_n$
with the following properties:
-
(a) If
 $y \in \mathcal {I}_n$
and
$y \in \mathcal {I}_n$
and
 $\mathcal {A}_{ij}(y)\cap \mathcal {A}(z)\neq \varnothing $
for some
$\mathcal {A}_{ij}(y)\cap \mathcal {A}(z)\neq \varnothing $
for some
 $z \in \mathcal {I}_n$
then
$z \in \mathcal {I}_n$
then
 $\tau _{ij}(y)= z$
.
$\tau _{ij}(y)= z$
. -
(b) If
 $y \in \mathcal {I}_n$
and
$y \in \mathcal {I}_n$
and
 $\mathcal {A}_{ij}(y)\cap \mathcal {A}(z)=\varnothing $
for all
$\mathcal {A}_{ij}(y)\cap \mathcal {A}(z)=\varnothing $
for all
 $z \in \mathcal {I}_n$
then
$z \in \mathcal {I}_n$
then
 $\tau _{ij}(y)= y$
.
$\tau _{ij}(y)= y$
.
Moreover, if
![]() $y \in \mathcal {I}_n$
and
$y \in \mathcal {I}_n$
and
![]() $y \neq \tau _{ij}(y)=z$
, then
$y \neq \tau _{ij}(y)=z$
, then
![]() $y(i) \neq z(i)$
and
$y(i) \neq z(i)$
and
![]() $y(j)\neq z(j)$
.
$y(j)\neq z(j)$
.
This result has an extension for affine symmetric groups; see [Reference Marberg30, Reference Marberg and Zhang34].
Remark The operators
![]() $\tau _{ij}$
, which first appeared in [Reference Incitti21], can be given a more explicit definition; see [Reference Hamaker, Marberg and Pawlowski14, Table 1]. However, our present applications only require the properties in the theorem.
$\tau _{ij}$
, which first appeared in [Reference Incitti21], can be given a more explicit definition; see [Reference Hamaker, Marberg and Pawlowski14, Table 1]. However, our present applications only require the properties in the theorem.
For
![]() $y \in \mathcal {I}_n$
, let
$y \in \mathcal {I}_n$
, let
![]() $\hat \ell (y)$
denote the common value of
$\hat \ell (y)$
denote the common value of
![]() $\ell (w)$
for any
$\ell (w)$
for any
![]() $w \in \mathcal {A}(y)$
. This is also the size of any
$w \in \mathcal {A}(y)$
. This is also the size of any
![]() $D \in \mathcal {ID}(y)$
. By Lemma 4.17, if
$D \in \mathcal {ID}(y)$
. By Lemma 4.17, if
![]() $y,z \in \mathcal {I}_n$
and
$y,z \in \mathcal {I}_n$
and
![]() $y< z$
then
$y< z$
then
![]() $\hat \ell (y) < \hat \ell (z)$
. Let
$\hat \ell (y) < \hat \ell (z)$
. Let
for
![]() $y \in \mathcal {I}_n$
and
$y \in \mathcal {I}_n$
and
![]() $j \in [n]$
. Since
$j \in [n]$
. Since
![]() $S_n \subset S_{n+1}$
and
$S_n \subset S_{n+1}$
and
![]() $\mathcal {I}_n \subset \mathcal {I}_{n+1}$
, this set is well-defined.
$\mathcal {I}_n \subset \mathcal {I}_{n+1}$
, this set is well-defined.
Theorem 4.23 Let
![]() $(j,i) $
be an outer corner of
$(j,i) $
be an outer corner of
![]() $y \in \mathcal {I}_n$
with
$y \in \mathcal {I}_n$
with
![]() $i\leq j$
.
$i\leq j$
.
-
(a) The map
 $D \mapsto D \sqcup \{(j,i)\}$
is a bijection
$D \mapsto D \sqcup \{(j,i)\}$
is a bijection
 $ \mathcal {ID}(y) \to \bigsqcup _{z \in \Psi (y,j)} \mathcal {ID}(z) $
.
$ \mathcal {ID}(y) \to \bigsqcup _{z \in \Psi (y,j)} \mathcal {ID}(z) $
. -
(b) If
 $i+j \leq n$
then
$i+j \leq n$
then
 $\Psi (y,j) \subset \mathcal {I}_n$
.
$\Psi (y,j) \subset \mathcal {I}_n$
.
Proof We have
![]() $y(j) = i$
and
$y(j) = i$
and
![]() $y(i) = j$
by Lemma 4.2. Suppose
$y(i) = j$
by Lemma 4.2. Suppose
![]() $v \in \mathcal {A}(y)$
and
$v \in \mathcal {A}(y)$
and
![]() $D \in \mathcal {PD}(v) \cap \mathcal {ID}(y)$
. By considering the pipes crossing at position
$D \in \mathcal {PD}(v) \cap \mathcal {ID}(y)$
. By considering the pipes crossing at position
![]() $(j,i)$
in the wiring diagram of D, as in the proof of Lemma 4.2, it follows that
$(j,i)$
in the wiring diagram of D, as in the proof of Lemma 4.2, it follows that
![]() $D\sqcup \{(j,i)\}$
is a reduced pipe dream for a permutation w that belongs to
$D\sqcup \{(j,i)\}$
is a reduced pipe dream for a permutation w that belongs to
![]() $\mathcal {A}_{js}(y)$
for some
$\mathcal {A}_{js}(y)$
for some
![]() $j< s \leq n$
. Set
$j< s \leq n$
. Set
![]() $z = w^{-1}\circ w \in \mathcal {I}_n$
. We wish to show that
$z = w^{-1}\circ w \in \mathcal {I}_n$
. We wish to show that
![]() $w \in \mathcal {A}(z)$
, since if this holds then
$w \in \mathcal {A}(z)$
, since if this holds then
![]() $D\sqcup \{(j,i)\} \in \mathcal {ID}(z)$
and Theorem 4.22 implies that
$D\sqcup \{(j,i)\} \in \mathcal {ID}(z)$
and Theorem 4.22 implies that
![]() $z \in \Psi (y,j)$
.
$z \in \Psi (y,j)$
.
To this end, let
![]() $\tilde y \in \mathcal {I}_n$
be the dominant involution whose unique involution pipe dream is
$\tilde y \in \mathcal {I}_n$
be the dominant involution whose unique involution pipe dream is
![]() $\operatorname {shdom}(y) \sqcup \{(j,i)\}$
and let
$\operatorname {shdom}(y) \sqcup \{(j,i)\}$
and let
![]() $\tilde v \in \mathcal {A}(\tilde y)$
be the (unique) atom with
$\tilde v \in \mathcal {A}(\tilde y)$
be the (unique) atom with
![]() $\mathcal {ID}(\tilde y) \subseteq \mathcal {PD}(\tilde v) $
. Corollaries 4.9 and 4.18 imply that
$\mathcal {ID}(\tilde y) \subseteq \mathcal {PD}(\tilde v) $
. Corollaries 4.9 and 4.18 imply that
![]() $\tilde y \nless y$
,
$\tilde y \nless y$
,
![]() $\tilde v \leq w $
, and
$\tilde v \leq w $
, and
![]() $v< w$
since
$v< w$
since
![]() $\operatorname {shdom}(\tilde y) \not \subset \operatorname {shdom}(y)$
and
$\operatorname {shdom}(\tilde y) \not \subset \operatorname {shdom}(y)$
and
![]() $\operatorname {shdom}(\tilde y) \subseteq D\sqcup \{(j,i)\}$
. Hence, we have
$\operatorname {shdom}(\tilde y) \subseteq D\sqcup \{(j,i)\}$
. Hence, we have
![]() $ \tilde y = {\tilde v}^{-1} \circ \tilde v \leq w^{-1} \circ w=z $
and
$ \tilde y = {\tilde v}^{-1} \circ \tilde v \leq w^{-1} \circ w=z $
and
![]() $ y = v^{-1} \circ v \leq w^{-1} \circ w=z $
by Corollary 4.21. Putting these relations together gives
$ y = v^{-1} \circ v \leq w^{-1} \circ w=z $
by Corollary 4.21. Putting these relations together gives
![]() $\tilde y \nless y \leq z$
and
$\tilde y \nless y \leq z$
and
![]() $\tilde y \leq z$
, so we must have
$\tilde y \leq z$
, so we must have
![]() $y < z$
and
$y < z$
and
![]() $\ell (w) = \hat \ell (y)+1 \leq \hat \ell (z)$
, and therefore
$\ell (w) = \hat \ell (y)+1 \leq \hat \ell (z)$
, and therefore
![]() $w \in \mathcal {A}(z)$
.
$w \in \mathcal {A}(z)$
.
Thus, the map in part (a) at least has the desired codomain and is clearly injective. To show that it is also surjective, suppose
![]() $E \in \mathcal {ID}(z)$
for some
$E \in \mathcal {ID}(z)$
for some
![]() $z \in \Psi (y,j)$
. Lemma 4.17 implies some
$z \in \Psi (y,j)$
. Lemma 4.17 implies some
![]() $(l,k) \in E$
has
$(l,k) \in E$
has
![]() $E \setminus \{(l,k)\} \in \mathcal {ID}(y)$
. Let
$E \setminus \{(l,k)\} \in \mathcal {ID}(y)$
. Let
![]() $E' \in \mathcal {PD}(z)$
be the almost-symmetric reduced pipe dream with
$E' \in \mathcal {PD}(z)$
be the almost-symmetric reduced pipe dream with
![]() . If
. If
![]() $(j,i) \neq (l,k)$
then, since
$(j,i) \neq (l,k)$
then, since
![]() $\operatorname {dom}(y) = \operatorname {shdom}(y) \cup \operatorname {shdom}(y)^T \subset E'$
, it would follow by considering the wiring diagram of
$\operatorname {dom}(y) = \operatorname {shdom}(y) \cup \operatorname {shdom}(y)^T \subset E'$
, it would follow by considering the wiring diagram of
![]() $E'$
that
$E'$
that
![]() $z(j) = i = y(j)$
, contradicting the last assertion in Theorem 4.22. Thus
$z(j) = i = y(j)$
, contradicting the last assertion in Theorem 4.22. Thus
![]() $(j,i) = (l,k)$
so the map in part (a) is surjective. Part (b) holds because an involution belongs to
$(j,i) = (l,k)$
so the map in part (a) is surjective. Part (b) holds because an involution belongs to
![]() $\mathcal {I}_n$
if any of its involution pipe dreams is contained in
$\mathcal {I}_n$
if any of its involution pipe dreams is contained in
![]() $\{ (j,i) : i\leq j\text { and }i +j \leq n\}$
.▪
$\{ (j,i) : i\leq j\text { and }i +j \leq n\}$
.▪
Example 4.24 If
![]() $y = 35142 \in \mathcal {I}_5$
then
$y = 35142 \in \mathcal {I}_5$
then

so the transpose of
![]() $\operatorname {shdom}(y)$
is the shifted Ferrers diagram of the partition
$\operatorname {shdom}(y)$
is the shifted Ferrers diagram of the partition
![]() $\lambda = (2,1)$
, and
$\lambda = (2,1)$
, and
![]() $(3,1)$
is an outer corner. One can show that
$(3,1)$
is an outer corner. One can show that
![]() $\Psi (y,3) = \{53241,45312\}$
. As predicted by Theorem 4.23 with
$\Psi (y,3) = \{53241,45312\}$
. As predicted by Theorem 4.23 with
![]() $(j,i) = (3,1)$
, both elements of
$(j,i) = (3,1)$
, both elements of
![]() $\Psi (y,3)$
are dominant with
$\Psi (y,3)$
are dominant with
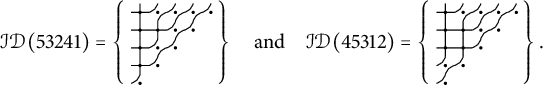
We may finally prove the pipe dream formula in Theorem 1.5 for the polynomials
![]() $\hat {\mathfrak {S}}_y$
.
$\hat {\mathfrak {S}}_y$
.
Theorem 4.25 If
![]() $z \in \mathcal {I}_n$
then
$z \in \mathcal {I}_n$
then
![]() $\hat {\mathfrak {S}}_z = \sum _{D \in \mathcal {ID}(z)} \prod _{(i,j) \in D} 2^{-\delta _{ij}}(x_i+x_j)$
.
$\hat {\mathfrak {S}}_z = \sum _{D \in \mathcal {ID}(z)} \prod _{(i,j) \in D} 2^{-\delta _{ij}}(x_i+x_j)$
.
Proof We abbreviate by setting
![]() $x_{(i,j)} = 2^{-\delta _{ij}}(x_i+x_j)$
, so that
$x_{(i,j)} = 2^{-\delta _{ij}}(x_i+x_j)$
, so that
![]() $x_{(i,j)} = x_i$
if
$x_{(i,j)} = x_i$
if
![]() $i=j$
and otherwise
$i=j$
and otherwise
![]() $x_{(i,j)} = x_i+x_j$
. It follows from [Reference Hamaker, Marberg and Pawlowski14, Theorem 3.30] that if
$x_{(i,j)} = x_i+x_j$
. It follows from [Reference Hamaker, Marberg and Pawlowski14, Theorem 3.30] that if
![]() is an outer corner of
is an outer corner of
![]() $z \in \mathcal {I}_n$
then
$z \in \mathcal {I}_n$
then
On the other hand, results of Wyser and Yong [Reference Wyser and Yong45] (see [Reference Hamaker, Marberg and Pawlowski13, Theorem 1.3]) show that
Let
![]() $\mathfrak {A}_z = \sum _{D \in \mathcal {ID}(z)} \prod _{(i,j) \in D} x_{(i,j)}$
. We show that
$\mathfrak {A}_z = \sum _{D \in \mathcal {ID}(z)} \prod _{(i,j) \in D} x_{(i,j)}$
. We show that
![]() $\hat {\mathfrak {S}}_z = \mathfrak {A}_z$
by downward induction on
$\hat {\mathfrak {S}}_z = \mathfrak {A}_z$
by downward induction on
![]() $\hat \ell (z)$
. If
$\hat \ell (z)$
. If
![]() $\hat \ell (z) = \max \{\hat \ell (y): y \in \mathcal {I}_n\}$
then
$\hat \ell (z) = \max \{\hat \ell (y): y \in \mathcal {I}_n\}$
then
![]() $z=n\cdots 321$
and the desired identity is equivalent to (4.3) since
$z=n\cdots 321$
and the desired identity is equivalent to (4.3) since
![]() $n\cdots 321$
is dominant. Otherwise, the transpose of
$n\cdots 321$
is dominant. Otherwise, the transpose of
![]() $\operatorname {shdom}(z)$
is a proper subset of
$\operatorname {shdom}(z)$
is a proper subset of
![]() $\operatorname {shdom}(n\cdots 321)^T=\mathsf {SD}_{(n-1,n-3,n-5,\dots )}$
by Corollary 4.18, so z must have an outer corner
$\operatorname {shdom}(n\cdots 321)^T=\mathsf {SD}_{(n-1,n-3,n-5,\dots )}$
by Corollary 4.18, so z must have an outer corner
![]() $(j,i)$
with
$(j,i)$
with
![]() $i\leq j$
and
$i\leq j$
and
![]() $i+j \leq n$
. In this case, we have
$i+j \leq n$
. In this case, we have
by (4.2), induction, and Theorem 4.23. Dividing by
![]() $x_{(i,j)}$
completes the proof.▪
$x_{(i,j)}$
completes the proof.▪
Example 4.26 Continuing Example 4.24, we have
and
so
4.3 Fixed-point-free involution pipe dream formulas
In this section, we assume n is even. Recall that
![]() .
.
Definition 4.27 The strictly shifted dominant component of
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is the set
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is the set
![]() which is also equal to
which is also equal to
![]() for all
for all
![]() $D \in \mathcal {PD}(z)$
by Proposition 4.11.
$D \in \mathcal {PD}(z)$
by Proposition 4.11.
Corollary 4.28 If
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
![]() $\operatorname {shdom}^{\neq }(z)$
is the maximal lower set of the poset
$\operatorname {shdom}^{\neq }(z)$
is the maximal lower set of the poset
![]() contained in some (equivalently, every)
contained in some (equivalently, every)
![]() $D \in \mathcal {FD}(z)$
.
$D \in \mathcal {FD}(z)$
.
Proof This is clear from Proposition 4.11.▪
For subsets
![]() $D \subseteq \mathbb {Z}\times \mathbb {Z}$
, define
$D \subseteq \mathbb {Z}\times \mathbb {Z}$
, define
![]() $D^\uparrow = \{ (i-1,j): (i,j) \in D\}$
and
$D^\uparrow = \{ (i-1,j): (i,j) \in D\}$
and
![]() $D^{\uparrow T} = (D^{\uparrow })^T.$
For example, if we have
$D^{\uparrow T} = (D^{\uparrow })^T.$
For example, if we have
![]() $z =465132 \in \mathcal {I}^{\mathsf {{FPF}}}_6$
then the Rothe diagram is
$z =465132 \in \mathcal {I}^{\mathsf {{FPF}}}_6$
then the Rothe diagram is
 $$ \begin{align*} D(z)= \left\{\begin{smallmatrix} + & + & + & 1 & \cdot & \cdot \\ + & + & + & \cdot & + & 1 \\ + & + & + & \cdot & 1 & \cdot \\ 1 & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & + & 1 & \cdot & \cdot & \cdot \\ \cdot & 1 & \cdot & \cdot & \cdot & \cdot \end{smallmatrix}\right\} \end{align*} $$
$$ \begin{align*} D(z)= \left\{\begin{smallmatrix} + & + & + & 1 & \cdot & \cdot \\ + & + & + & \cdot & + & 1 \\ + & + & + & \cdot & 1 & \cdot \\ 1 & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & + & 1 & \cdot & \cdot & \cdot \\ \cdot & 1 & \cdot & \cdot & \cdot & \cdot \end{smallmatrix}\right\} \end{align*} $$
with each one indicating a position
![]() $(i,j) \in [n]\times [n]$
with
$(i,j) \in [n]\times [n]$
with
![]() $z(i) =j$
and each
$z(i) =j$
and each
![]() $+$
indicating a position in
$+$
indicating a position in
![]() $ D(z)$
. The relevant dominant components are
$ D(z)$
. The relevant dominant components are
As we see in this example, if
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is any fixed-point-free involution, then
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is any fixed-point-free involution, then
![]() $(\operatorname {shdom}^{\neq }(z))^{\uparrow T} $
is the shifted Ferrers diagram of some strict partition. Moreover, a pair
$(\operatorname {shdom}^{\neq }(z))^{\uparrow T} $
is the shifted Ferrers diagram of some strict partition. Moreover, a pair
![]() is an outer corner of z if and only if
is an outer corner of z if and only if
![]() $(\operatorname {shdom}^{\neq }(D) \sqcup \{(j,i)\})^{\uparrow T} $
is again a shifted Ferrers diagram, in which case
$(\operatorname {shdom}^{\neq }(D) \sqcup \{(j,i)\})^{\uparrow T} $
is again a shifted Ferrers diagram, in which case
![]() $z(j) = i$
by Lemma 4.2. The unique outer corner of
$z(j) = i$
by Lemma 4.2. The unique outer corner of
![]() $z = 465132$
in
$z = 465132$
in
![]() is
is
![]() $(4,1)$
.
$(4,1)$
.
Definition 4.29 An element
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is fpf-dominant if
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is fpf-dominant if
![]() $\operatorname {shdom}^{\neq }(z) \in \mathcal {FD}(z)$
.
$\operatorname {shdom}^{\neq }(z) \in \mathcal {FD}(z)$
.
This condition does not imply that z is dominant in the sense of being
![]() $132$
-avoiding. For example,
$132$
-avoiding. For example,
![]() $z=s_1s_3\cdots s_{n-1} = 2143\cdots n(n-1) \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is always fpf-dominant as
$z=s_1s_3\cdots s_{n-1} = 2143\cdots n(n-1) \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is always fpf-dominant as
![]() $\operatorname {shdom}^{\neq }(z) = \varnothing $
.
$\operatorname {shdom}^{\neq }(z) = \varnothing $
.
Lemma 4.30 If
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is fpf-dominant then
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is fpf-dominant then
![]() $\mathcal {FD}(z) = \{ \operatorname {shdom}^{\neq }(z)\}.$
$\mathcal {FD}(z) = \{ \operatorname {shdom}^{\neq }(z)\}.$
Proof This holds since
![]() $\operatorname {shdom}^{\neq }(z) \subseteq D$
for all
$\operatorname {shdom}^{\neq }(z) \subseteq D$
for all
![]() $D \in \mathcal {FD}(z)$
by Proposition 4.11.▪
$D \in \mathcal {FD}(z)$
by Proposition 4.11.▪
Proposition 4.31 If
![]() $\lambda $
is a strict partition with
$\lambda $
is a strict partition with
![]() $\lambda \subseteq (n-2,n-4,\dots ,4,2)$
then there exists a unique fpf-dominant
$\lambda \subseteq (n-2,n-4,\dots ,4,2)$
then there exists a unique fpf-dominant
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
with
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
with
![]() $(\operatorname {shdom}^{\neq }(z))^{\uparrow T} := \{ (j, i-1) : (i,j) \in \operatorname {shdom}^{\neq }(z)\} = \mathsf {SD}_\lambda $
.
$(\operatorname {shdom}^{\neq }(z))^{\uparrow T} := \{ (j, i-1) : (i,j) \in \operatorname {shdom}^{\neq }(z)\} = \mathsf {SD}_\lambda $
.
Proof Uniqueness is clear from Lemma 4.30. If
![]() $\lambda \subseteq (n-2,n-4,\dots ,2)$
is empty then take
$\lambda \subseteq (n-2,n-4,\dots ,2)$
is empty then take
![]() $z=1^{\mathsf {{FPF}}}_n$
. Otherwise, let
$z=1^{\mathsf {{FPF}}}_n$
. Otherwise, let
![]() $\mu \subset \lambda $
be a strict partition such that
$\mu \subset \lambda $
be a strict partition such that
![]() $ \mathsf {SD}_\lambda = \mathsf {SD}_\mu \sqcup \{(i,j-1)\}$
where
$ \mathsf {SD}_\lambda = \mathsf {SD}_\mu \sqcup \{(i,j-1)\}$
where
![]() $i< j$
. By induction, there exists an fpf-dominant
$i< j$
. By induction, there exists an fpf-dominant
![]() $y \in \mathcal {I}^{\mathsf {{FPF}}}_n$
with
$y \in \mathcal {I}^{\mathsf {{FPF}}}_n$
with
![]() $(\operatorname {shdom}^{\neq }(y))^{\uparrow T} = \mathsf {SD}_\mu $
. Let
$(\operatorname {shdom}^{\neq }(y))^{\uparrow T} = \mathsf {SD}_\mu $
. Let
![]() $D \in \mathcal {PD}(y)$
be symmetric with
$D \in \mathcal {PD}(y)$
be symmetric with
![]() . Lemmas 3.11 and 4.2 imply that
. Lemmas 3.11 and 4.2 imply that
![]() $ D \sqcup \{(j,i),(i,j)\}$
is a symmetric reduced pipe dream for some
$ D \sqcup \{(j,i),(i,j)\}$
is a symmetric reduced pipe dream for some
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
, which is the desired element.▪
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
, which is the desired element.▪
If
![]() $y,z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
, then
$y,z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
, then
![]() $y \leq z$
in Bruhat order if and only if some (equivalently, every) fpf-involution word for z contains a subword that is an fpf-involution word for y [Reference Hamaker, Marberg and Pawlowski14, Theorem 4.6]. From this and Theorem 3.12 we deduce the following:
$y \leq z$
in Bruhat order if and only if some (equivalently, every) fpf-involution word for z contains a subword that is an fpf-involution word for y [Reference Hamaker, Marberg and Pawlowski14, Theorem 4.6]. From this and Theorem 3.12 we deduce the following:
Lemma 4.32 Suppose
![]() $y,z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
. Then
$y,z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
. Then
![]() $y \leq z$
if and only if some (equivalently, every) fpf-involution pipe dream for z has a subset that is an fpf-involution pipe dream for y.
$y \leq z$
if and only if some (equivalently, every) fpf-involution pipe dream for z has a subset that is an fpf-involution pipe dream for y.
Corollary 4.33 Let
![]() $y,z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
where y is fpf-dominant. Then
$y,z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
where y is fpf-dominant. Then
![]() $y\leq z$
if and only if
$y\leq z$
if and only if
![]() $\operatorname {shdom}^{\neq }(y) \subseteq D$
for some (equivalently, every)
$\operatorname {shdom}^{\neq }(y) \subseteq D$
for some (equivalently, every)
![]() $D \in \mathcal {FD}(z)$
.
$D \in \mathcal {FD}(z)$
.
Proof This is clear since if
![]() $y \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is fpf-dominant then
$y \in \mathcal {I}^{\mathsf {{FPF}}}_n$
is fpf-dominant then
![]() $|\mathcal {FD}(y)|=1$
.▪
$|\mathcal {FD}(y)|=1$
.▪
For
![]() $y \in \mathcal {I}^{\mathsf {{FPF}}}_n$
and
$y \in \mathcal {I}^{\mathsf {{FPF}}}_n$
and
![]() $j \in [n]$
, define
$j \in [n]$
, define
![]() $ \Psi ^{\mathsf {{FPF}}}(y,j)$
to be the set of fixed-point-free involutions
$ \Psi ^{\mathsf {{FPF}}}(y,j)$
to be the set of fixed-point-free involutions
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_{n+2}$
with length
$z \in \mathcal {I}^{\mathsf {{FPF}}}_{n+2}$
with length
![]() $\ell (z) = \ell (y)+2$
that can be written as
$\ell (z) = \ell (y)+2$
that can be written as
![]() $z = t_{js}\cdot ys_{n+1} \cdot t_{js}$
for an integer s with
$z = t_{js}\cdot ys_{n+1} \cdot t_{js}$
for an integer s with
![]() $j < s \leq n+2$
. We have an analogue of Theorem 4.23:
$j < s \leq n+2$
. We have an analogue of Theorem 4.23:
Theorem 4.34 Let
![]() $(j,i)$
be an outer corner of
$(j,i)$
be an outer corner of
![]() $y \in \mathcal {I}^{\mathsf {{FPF}}}_n$
with
$y \in \mathcal {I}^{\mathsf {{FPF}}}_n$
with
![]() $i< j$
.
$i< j$
.
-
(a) The map
 $D \mapsto D \sqcup \{(j,i)\}$
is a bijection
$D \mapsto D \sqcup \{(j,i)\}$
is a bijection
 $ \mathcal {FD}(y) \to \bigsqcup _{z \in \Psi ^{\mathsf {{FPF}}}(y,j)} \mathcal {FD}(z). $
$ \mathcal {FD}(y) \to \bigsqcup _{z \in \Psi ^{\mathsf {{FPF}}}(y,j)} \mathcal {FD}(z). $
-
(b) If
 $i+j \leq n$
then
$i+j \leq n$
then
 $ \Psi ^{\mathsf {{FPF}}}(y,j)\subset \left \{ z s_{n+1} : z \in \mathcal {I}^{\mathsf {{FPF}}}_{n}\right \}$
.
$ \Psi ^{\mathsf {{FPF}}}(y,j)\subset \left \{ z s_{n+1} : z \in \mathcal {I}^{\mathsf {{FPF}}}_{n}\right \}$
.
Proof Our argument is similar to the proof of Theorem 4.23. Choose
![]() $D \in \mathcal {FD}(y) = \mathcal {FD}(ys_{n+1})$
. Suppose
$D \in \mathcal {FD}(y) = \mathcal {FD}(ys_{n+1})$
. Suppose
![]() $D' \in \mathcal {PD}(ys_{n+1})$
is the symmetric reduced pipe dream with
$D' \in \mathcal {PD}(ys_{n+1})$
is the symmetric reduced pipe dream with
![]() and set
and set
![]() $E = D\sqcup \{(j,i)\}$
and
$E = D\sqcup \{(j,i)\}$
and
![]() $E' = D' \sqcup \{(i,j),(j,i)\}$
. It follows from Lemmas 3.11 and 4.2 that
$E' = D' \sqcup \{(i,j),(j,i)\}$
. It follows from Lemmas 3.11 and 4.2 that
![]() $E'$
is a reduced pipe dream for some element
$E'$
is a reduced pipe dream for some element
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_{n+2}$
. Since
$z \in \mathcal {I}^{\mathsf {{FPF}}}_{n+2}$
. Since
![]() $E'$
is symmetric, one has
$E'$
is symmetric, one has
![]() . Finally, by considering the pipes crossing at position
. Finally, by considering the pipes crossing at position
![]() $(j,i)$
in E we deduce that
$(j,i)$
in E we deduce that
![]() $z \in \Psi ^{\mathsf {{FPF}}}(y,j)$
.
$z \in \Psi ^{\mathsf {{FPF}}}(y,j)$
.
Thus
![]() $D \mapsto D \sqcup \{(j,i)\}$
is a well-defined map
$D \mapsto D \sqcup \{(j,i)\}$
is a well-defined map
![]() $\mathcal {FD}(y) \to \bigsqcup _{z\in \Psi ^{\mathsf {{FPF}}}(y,j)} \mathcal {FD}(z)$
. This map is clearly injective. To show that it is also surjective, suppose
$\mathcal {FD}(y) \to \bigsqcup _{z\in \Psi ^{\mathsf {{FPF}}}(y,j)} \mathcal {FD}(z)$
. This map is clearly injective. To show that it is also surjective, suppose
![]() $E \in \mathcal {FD}(z)$
for some
$E \in \mathcal {FD}(z)$
for some
![]() $z \in \Psi ^{\mathsf {{FPF}}}(y,j)$
. Lemma 4.32 implies that there exists a position
$z \in \Psi ^{\mathsf {{FPF}}}(y,j)$
. Lemma 4.32 implies that there exists a position
![]() $(l,k) \in E$
such that
$(l,k) \in E$
such that
![]() $E \setminus \{(l,k)\} \in \mathcal {FD}(y)$
. If
$E \setminus \{(l,k)\} \in \mathcal {FD}(y)$
. If
![]() $(j,i) \neq (l,k)$
then it would follow as in the proof Theorem 4.23 that
$(j,i) \neq (l,k)$
then it would follow as in the proof Theorem 4.23 that
![]() $z(j) = y(j)=ys_{n+1}(j)=i$
, which is impossible if
$z(j) = y(j)=ys_{n+1}(j)=i$
, which is impossible if
![]() $z = t_{js}\cdot ys_{n+1}\cdot t_{js}$
where
$z = t_{js}\cdot ys_{n+1}\cdot t_{js}$
where
![]() $i =y(j) < j < s \leq n + 2$
. Thus
$i =y(j) < j < s \leq n + 2$
. Thus
![]() $(j,i) = (l,k)$
so the map in part (a) is also surjective. Part (b) holds because
$(j,i) = (l,k)$
so the map in part (a) is also surjective. Part (b) holds because
![]() $\left \{ zs_{n+1} : z \in \mathcal {I}^{\mathsf {{FPF}}}_{n}\right \}$
contains all involutions in
$\left \{ zs_{n+1} : z \in \mathcal {I}^{\mathsf {{FPF}}}_{n}\right \}$
contains all involutions in
![]() $\mathcal {I}^{\mathsf {{FPF}}}_{n+2}$
with fpf-involution pipe dreams that are subsets of
$\mathcal {I}^{\mathsf {{FPF}}}_{n+2}$
with fpf-involution pipe dreams that are subsets of
![]() $\{ (j,i) : i\leq j, i +j \leq n\}$
.▪
$\{ (j,i) : i\leq j, i +j \leq n\}$
.▪
Example 4.35 If
![]() $y = 351624 \in \mathcal {I}^{\mathsf {{FPF}}}_6$
then
$y = 351624 \in \mathcal {I}^{\mathsf {{FPF}}}_6$
then
so
![]() $\operatorname {shdom}(y)=\{(2,1)\}$
, and
$\operatorname {shdom}(y)=\{(2,1)\}$
, and
![]() $(3,1)$
is an outer corner. In this case,
$(3,1)$
is an outer corner. In this case,
![]() $ \Psi ^{\mathsf {{FPF}}}(y,3) = \{532614,456123\}$
. As predicted by the theorem with
$ \Psi ^{\mathsf {{FPF}}}(y,3) = \{532614,456123\}$
. As predicted by the theorem with
![]() $(j,i) = (3,1)$
, both elements of
$(j,i) = (3,1)$
, both elements of
![]() $ \Psi ^{\mathsf {{FPF}}}(y,3)$
are fpf-dominant since
$ \Psi ^{\mathsf {{FPF}}}(y,3)$
are fpf-dominant since
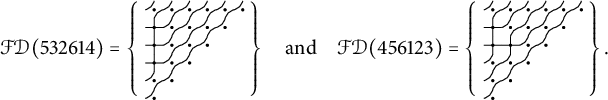
We may now prove the second half of Theorem 1.5, concerning
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
.
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
.
Theorem 4.36 If
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z = \sum _{D \in \mathcal {FD}(z)} \prod _{(i,j) \in D} (x_i + x_j)$
.
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z = \sum _{D \in \mathcal {FD}(z)} \prod _{(i,j) \in D} (x_i + x_j)$
.
Proof [Reference Hamaker, Marberg and Pawlowski14, Theorem 4.17] implies that if
![]() is an outer corner of
is an outer corner of
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
Moreover, as n is even, [Reference Hamaker, Marberg and Pawlowski13, Theorem 1.3] implies that we have
Let
![]() $\mathfrak {B}_z = \sum _{D \in \mathcal {FD}(z)} \prod _{(i,j) \in D} (x_i+x_j)$
. If
$\mathfrak {B}_z = \sum _{D \in \mathcal {FD}(z)} \prod _{(i,j) \in D} (x_i+x_j)$
. If
![]() $\ell (z) = \max \left \{\ell (y): y \in \mathcal {I}^{\mathsf {{FPF}}}_n\right \}$
then
$\ell (z) = \max \left \{\ell (y): y \in \mathcal {I}^{\mathsf {{FPF}}}_n\right \}$
then
![]() $z=n\cdots 321$
and the identity
$z=n\cdots 321$
and the identity
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z = \mathfrak {B}_z$
is equivalent to (4.5). Otherwise, the transpose of
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z = \mathfrak {B}_z$
is equivalent to (4.5). Otherwise, the transpose of
![]() $\operatorname {shdom}^{\neq }(z)$
shifted up one row is a proper subset of
$\operatorname {shdom}^{\neq }(z)$
shifted up one row is a proper subset of
![]() $\operatorname {shdom}^{\neq }(n\cdots 321)^{\uparrow T}=\mathsf {SD}_{(n-2,n-4,\dots ,4,2)}$
by Corollary 4.33, so z has an outer corner
$\operatorname {shdom}^{\neq }(n\cdots 321)^{\uparrow T}=\mathsf {SD}_{(n-2,n-4,\dots ,4,2)}$
by Corollary 4.33, so z has an outer corner
![]() with
with
![]() $i+j \leq n$
. In this case,
$i+j \leq n$
. In this case,
![]() $(x_i+x_j) \hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z = \sum _{u \in \Psi ^{\mathsf {{FPF}}}(z,j)} \hat {\mathfrak {S}}^{\mathsf {{FPF}}}_u= \sum _{u \in \Psi ^{\mathsf {{FPF}}}(z,j)} \mathfrak {B}_u = (x_i+x_j) \mathfrak {B}_z$
by (4.4), induction, and Theorem 4.34. Dividing by
$(x_i+x_j) \hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z = \sum _{u \in \Psi ^{\mathsf {{FPF}}}(z,j)} \hat {\mathfrak {S}}^{\mathsf {{FPF}}}_u= \sum _{u \in \Psi ^{\mathsf {{FPF}}}(z,j)} \mathfrak {B}_u = (x_i+x_j) \mathfrak {B}_z$
by (4.4), induction, and Theorem 4.34. Dividing by
![]() $x_i+x_j$
completes the proof.▪
$x_i+x_j$
completes the proof.▪
Example 4.37 Continuing Example 4.35, we have
and
so
5 Generating pipe dreams
Bergeron and Billey [Reference Bergeron and Billey1] proved that the set
![]() $\mathcal {PD}(w)$
is generated by applying simple transformations to a unique “bottom” pipe dream. Here, we derive versions of this result for the sets of involution pipe dreams
$\mathcal {PD}(w)$
is generated by applying simple transformations to a unique “bottom” pipe dream. Here, we derive versions of this result for the sets of involution pipe dreams
![]() $\mathcal {ID}(y)$
and
$\mathcal {ID}(y)$
and
![]() $\mathcal {FD}(z)$
. This leads to algorithms for computing the sets
$\mathcal {FD}(z)$
. This leads to algorithms for computing the sets
![]() $\mathcal {ID}(y)$
and
$\mathcal {ID}(y)$
and
![]() $\mathcal {FD}(z)$
that are much more efficient than the naive methods suggested by our original definitions.
$\mathcal {FD}(z)$
that are much more efficient than the naive methods suggested by our original definitions.
5.1 Ladder moves
Let D and E be subsets of
![]() $\mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
, depicted as positions marked by “
$\mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
, depicted as positions marked by “
![]() $+$
” in a matrix. If E is obtained from D by replacing a subset of the form
$+$
” in a matrix. If E is obtained from D by replacing a subset of the form
 $$ \begin{align*} \begin{array}{cc} \cdot & \cdot \\ + & + \\ \vdots & \vdots \\ + & + \\ + & \cdot \end{array} \qquad\text{by}\qquad \begin{array}{cc} \cdot & + \\ + & + \\ \vdots & \vdots \\ + & + \\ \cdot & \cdot \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{cc} \cdot & \cdot \\ + & + \\ \vdots & \vdots \\ + & + \\ + & \cdot \end{array} \qquad\text{by}\qquad \begin{array}{cc} \cdot & + \\ + & + \\ \vdots & \vdots \\ + & + \\ \cdot & \cdot \end{array} \end{align*} $$
then we say that E is obtained from D by a ladder move and write
![]() $D \lessdot _{\mathcal {PD}} E$
. More formally:
$D \lessdot _{\mathcal {PD}} E$
. More formally:
Definition 5.1 We write
![]() $D \lessdot _{\mathcal {PD}} E$
if for some integers
$D \lessdot _{\mathcal {PD}} E$
if for some integers
![]() $i< j$
and k the following holds:
$i< j$
and k the following holds:
-
• One has
 $\{i+1,i+2,\dots ,j-1\}\times \{k,k+1\} \subset D$
.
$\{i+1,i+2,\dots ,j-1\}\times \{k,k+1\} \subset D$
. -
• It holds that
 $(j,k) \in D$
but
$(j,k) \in D$
but
 $(i,k),(i,k+1),(j,k+1)\notin D$
.
$(i,k),(i,k+1),(j,k+1)\notin D$
. -
• One has
 $E = D\setminus \{(j,k)\} \cup \{(i,k+1)\}$
.
$E = D\setminus \{(j,k)\} \cup \{(i,k+1)\}$
.
One can have
![]() $i+1=j$
in this definition, in which case the first condition holds vacuously. Let
$i+1=j$
in this definition, in which case the first condition holds vacuously. Let
![]() $<_{\mathcal {PD}}$
be the transitive closure of
$<_{\mathcal {PD}}$
be the transitive closure of
![]() $\lessdot _{\mathcal {PD}}$
. This relation is a strict partial order. Let
$\lessdot _{\mathcal {PD}}$
. This relation is a strict partial order. Let
![]() $\sim _{\mathcal {PD}}$
denote the symmetric closure of the partial order
$\sim _{\mathcal {PD}}$
denote the symmetric closure of the partial order
![]() $\leq _{\mathcal {PD}}$
.
$\leq _{\mathcal {PD}}$
.
Recall the definition of the bottom pipe dream
![]() $D_{\text {bot}}(w)$
from (4.1).
$D_{\text {bot}}(w)$
from (4.1).
Theorem 5.2 ([Reference Bergeron and Billey1, Theorem 3.7])
Let
![]() $w \in S_n$
. Then
$w \in S_n$
. Then
Thus
![]() $\mathcal {PD}(w)$
is an upper and lower set of
$\mathcal {PD}(w)$
is an upper and lower set of
![]() $\leq _{\mathcal {PD}}$
, with unique minimum
$\leq _{\mathcal {PD}}$
, with unique minimum
![]() $D_{\text {bot}}(w)$
.
$D_{\text {bot}}(w)$
.
Define
![]() $\leq ^{\mathsf {chute}}_{\mathcal {PD}}$
to be the partial order with
$\leq ^{\mathsf {chute}}_{\mathcal {PD}}$
to be the partial order with
![]() $D \leq ^{\mathsf {chute}}_{\mathcal {PD}} E$
if and only if
$D \leq ^{\mathsf {chute}}_{\mathcal {PD}} E$
if and only if
![]() $E^T \leq _{\mathcal {PD}} D^T$
, and let
$E^T \leq _{\mathcal {PD}} D^T$
, and let
![]() $D_{\text {top}}(w) = D_{\text {bot}}(w^{-1})^T$
for
$D_{\text {top}}(w) = D_{\text {bot}}(w^{-1})^T$
for
![]() $w \in S_n$
. Then
$w \in S_n$
. Then
![]() $\mathcal {PD}(w)= \left \{ E : E \leq ^{\mathsf {chute}}_{\mathcal {PD}} D_{\text {top}}(w) \right \} $
by Corollary 3.8 and Theorem 5.2. Bergeron and Billey [Reference Bergeron and Billey1] refer to the covering relation in
$\mathcal {PD}(w)= \left \{ E : E \leq ^{\mathsf {chute}}_{\mathcal {PD}} D_{\text {top}}(w) \right \} $
by Corollary 3.8 and Theorem 5.2. Bergeron and Billey [Reference Bergeron and Billey1] refer to the covering relation in
![]() $\leq ^{\mathsf {chute}}_{\mathcal {PD}}$
as a chute move. In the next sections, we will see that there are natural versions of
$\leq ^{\mathsf {chute}}_{\mathcal {PD}}$
as a chute move. In the next sections, we will see that there are natural versions of
![]() $\leq _{\mathcal {PD}}$
and
$\leq _{\mathcal {PD}}$
and
![]() $D_{\text {bot}}(w)$
for (fpf-)involution pipe dreams. There do not seem to be good involution analogues of
$D_{\text {bot}}(w)$
for (fpf-)involution pipe dreams. There do not seem to be good involution analogues of
![]() $\leq ^{\mathsf {chute}}_{\mathcal {PD}}$
or
$\leq ^{\mathsf {chute}}_{\mathcal {PD}}$
or
![]() $D_{\text {top}}(w)$
, however.
$D_{\text {top}}(w)$
, however.
5.2 Involution ladder moves
To prove an analogue of Theorem 5.2 for involution pipe dreams, we need to introduce another partial order
![]() $<_{\mathcal {ID}}$
on subsets of
$<_{\mathcal {ID}}$
on subsets of
![]() $\mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
. Again let D and E be subsets of
$\mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
. Again let D and E be subsets of
![]() $\mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
. Informally, we define
$\mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
. Informally, we define
![]() $<_{\mathcal {ID}}$
to be the transitive closure of
$<_{\mathcal {ID}}$
to be the transitive closure of
![]() $\lessdot _{\mathcal {PD}}$
and the relation that has
$\lessdot _{\mathcal {PD}}$
and the relation that has
![]() $D \lessdot _{\mathcal {ID}} E$
whenever E is obtained from D by replacing a subset of the form
$D \lessdot _{\mathcal {ID}} E$
whenever E is obtained from D by replacing a subset of the form
 $$ \begin{align} \def\arraystretch{0.8} \begin{array}{cccccc} & & \nearrow & \nearrow & \nearrow & \nearrow \\ & \cdot & \cdot & \cdot & \cdot\\ \cdot & \cdot & \cdot & \cdot\\ + & \cdot & \cdot\\ + & + \\ \vdots & \vdots \\ + & + \\ + & \cdot & {\phantom{+}} & {\phantom +} & {\phantom+} \end{array} \qquad\text{by}\qquad \begin{array}{cccccc} & & \nearrow & \nearrow & \nearrow & \nearrow \\ & \cdot & \cdot & \cdot & \cdot\\ \cdot & \cdot & \cdot & \cdot\\ + & + & \cdot\\ + & + \\ \vdots & \vdots \\ + & + \\ \cdot & \cdot & {\phantom+} & {\phantom+} & {\phantom+} \end{array} \end{align} $$
$$ \begin{align} \def\arraystretch{0.8} \begin{array}{cccccc} & & \nearrow & \nearrow & \nearrow & \nearrow \\ & \cdot & \cdot & \cdot & \cdot\\ \cdot & \cdot & \cdot & \cdot\\ + & \cdot & \cdot\\ + & + \\ \vdots & \vdots \\ + & + \\ + & \cdot & {\phantom{+}} & {\phantom +} & {\phantom+} \end{array} \qquad\text{by}\qquad \begin{array}{cccccc} & & \nearrow & \nearrow & \nearrow & \nearrow \\ & \cdot & \cdot & \cdot & \cdot\\ \cdot & \cdot & \cdot & \cdot\\ + & + & \cdot\\ + & + \\ \vdots & \vdots \\ + & + \\ \cdot & \cdot & {\phantom+} & {\phantom+} & {\phantom+} \end{array} \end{align} $$
where the upper parts of the antidiagonals with
![]() $\nearrow $
must be empty. For example,
$\nearrow $
must be empty. For example,
 $$ \begin{align*} \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot\\ + & \cdot & \cdot & +\\ + & \cdot & \cdot& \cdot\\ \cdot& + & \cdot & \cdot \end{array} \ \lessdot_{\mathcal{ID}}\ \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot\\ + & + & \cdot & +\\ \cdot & \cdot & \cdot& \cdot\\ \cdot & + & \cdot & \cdot \end{array} \quad\text{and}\quad \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot\\ + & \cdot & \cdot & +\\ + & + & \cdot& \cdot\\ + & \cdot & \cdot & \cdot \end{array} \ \lessdot_{\mathcal{ID}}\ \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot\\ + & + & \cdot & +\\ + & + & \cdot& \cdot\\ \cdot & \cdot & \cdot & \cdot \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot\\ + & \cdot & \cdot & +\\ + & \cdot & \cdot& \cdot\\ \cdot& + & \cdot & \cdot \end{array} \ \lessdot_{\mathcal{ID}}\ \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot\\ + & + & \cdot & +\\ \cdot & \cdot & \cdot& \cdot\\ \cdot & + & \cdot & \cdot \end{array} \quad\text{and}\quad \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot\\ + & \cdot & \cdot & +\\ + & + & \cdot& \cdot\\ + & \cdot & \cdot & \cdot \end{array} \ \lessdot_{\mathcal{ID}}\ \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot\\ + & + & \cdot & +\\ + & + & \cdot& \cdot\\ \cdot & \cdot & \cdot & \cdot \end{array} \end{align*} $$
but
 $$ \begin{align*} \begin{array}{cccccc} \cdot & \cdot & + & \cdot\\ + & \cdot & \cdot & \cdot \\ + & + & \cdot& \cdot\\ + & \cdot & \cdot & \cdot \end{array} \ \nless _{\mathcal{ID}}\ \begin{array}{cccccc} \cdot & \cdot & + & \cdot\\ + & + & \cdot & \cdot\\ + & + & \cdot& \cdot\\ \cdot & \cdot & \cdot & \cdot \end{array} \quad\text{and}\quad \begin{array}{cccccc} \cdot & \cdot & \cdot & +\\ + & \cdot & \cdot & \cdot \\ + & + & \cdot& \cdot\\ + & \cdot & \cdot & \cdot \end{array} \ \nless _{\mathcal{ID}}\ \begin{array}{cccccc} \cdot & \cdot & \cdot & +\\ + & + & \cdot & \cdot\\ + & + & \cdot& \cdot\\ \cdot & \cdot & \cdot & \cdot \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{cccccc} \cdot & \cdot & + & \cdot\\ + & \cdot & \cdot & \cdot \\ + & + & \cdot& \cdot\\ + & \cdot & \cdot & \cdot \end{array} \ \nless _{\mathcal{ID}}\ \begin{array}{cccccc} \cdot & \cdot & + & \cdot\\ + & + & \cdot & \cdot\\ + & + & \cdot& \cdot\\ \cdot & \cdot & \cdot & \cdot \end{array} \quad\text{and}\quad \begin{array}{cccccc} \cdot & \cdot & \cdot & +\\ + & \cdot & \cdot & \cdot \\ + & + & \cdot& \cdot\\ + & \cdot & \cdot & \cdot \end{array} \ \nless _{\mathcal{ID}}\ \begin{array}{cccccc} \cdot & \cdot & \cdot & +\\ + & + & \cdot & \cdot\\ + & + & \cdot& \cdot\\ \cdot & \cdot & \cdot & \cdot \end{array} \end{align*} $$
since the relevant antidiagonals in (5.1) are not empty. The precise definition of
![]() $\lessdot _{\mathcal {ID}} $
is:
$\lessdot _{\mathcal {ID}} $
is:
Definition 5.3 We write
![]() $ D \lessdot _{\mathcal {ID}} E$
if for some integers
$ D \lessdot _{\mathcal {ID}} E$
if for some integers
![]() $i< j$
and k the following holds:
$i< j$
and k the following holds:
-
• One has
 $\{i+1,i+2,\dots ,j-1\}\times \{k,k+1\} \subset D$
.
$\{i+1,i+2,\dots ,j-1\}\times \{k,k+1\} \subset D$
. -
• It holds that
 $(i,k),(j,k) \in D$
but
$(i,k),(j,k) \in D$
but
 $(i,k+1),(i,k+2),(j,k+1)\notin D$
.
$(i,k+1),(i,k+2),(j,k+1)\notin D$
. -
• One has
 $E = D\setminus \{(j,k)\} \cup \{(i,k+1)\}$
.
$E = D\setminus \{(j,k)\} \cup \{(i,k+1)\}$
. -
• The set D contains no positions strictly northeast of and in the same antidiagonal as
 $(i,k-1)$
,
$(i,k-1)$
,
 $(i,k)$
,
$(i,k)$
,
 $(i,k+1)$
, or
$(i,k+1)$
, or
 $(i,k+2)$
.
$(i,k+2)$
.
One may again have
![]() $i+1=j$
, in which case the first condition holds vacuously. We define
$i+1=j$
, in which case the first condition holds vacuously. We define
![]() $<_{\mathcal {ID}}$
to be the transitive closure of
$<_{\mathcal {ID}}$
to be the transitive closure of
![]() $\lessdot _{\mathcal {PD}}$
and
$\lessdot _{\mathcal {PD}}$
and
![]() $\lessdot _{\mathcal {ID}}$
, and write
$\lessdot _{\mathcal {ID}}$
, and write
![]() $\sim _{\mathcal {ID}}$
for the symmetric closure of
$\sim _{\mathcal {ID}}$
for the symmetric closure of
![]() $\leq _{\mathcal {ID}}$
.
$\leq _{\mathcal {ID}}$
.
Our goal is to show that
![]() $<_{\mathcal {ID}}$
defines a partial order on
$<_{\mathcal {ID}}$
defines a partial order on
![]() $\mathcal {ID}(z)$
; for an example of this poset, see Figure 1. To proceed, we must recall a few nontrivial properties of the set
$\mathcal {ID}(z)$
; for an example of this poset, see Figure 1. To proceed, we must recall a few nontrivial properties of the set
![]() $\mathcal {A}(z)$
from Section 2.1.
$\mathcal {A}(z)$
from Section 2.1.
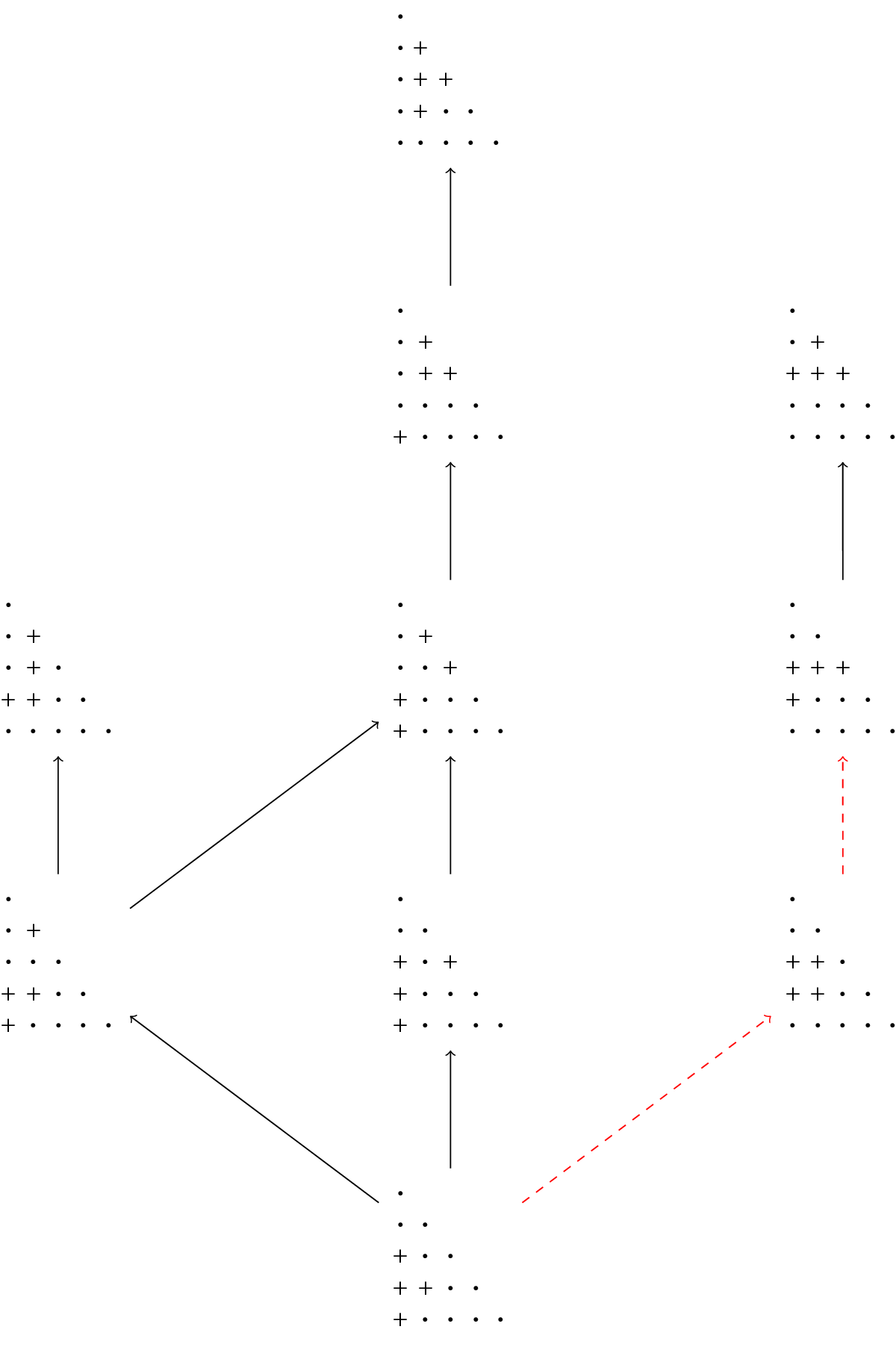
Figure 1: Hasse diagram of
![]() $(\mathcal {ID}(z), <_{\mathcal {ID}})$
for
$(\mathcal {ID}(z), <_{\mathcal {ID}})$
for
![]() $z=(3,6)(4,5) \in \mathcal {I}_6$
. The dashed red arrows indicate the covering relations of the form
$z=(3,6)(4,5) \in \mathcal {I}_6$
. The dashed red arrows indicate the covering relations of the form
![]() $D \lessdot _{\mathcal {ID}} E$
.
$D \lessdot _{\mathcal {ID}} E$
.
Lemma 5.4 ([Reference Hamaker, Marberg and Pawlowski12, Lemma 6.3])
Let
![]() $z \in \mathcal {I}_n$
and
$z \in \mathcal {I}_n$
and
![]() $w \in \mathcal {A}(z)$
. Then no subword
$w \in \mathcal {A}(z)$
. Then no subword
![]() $w(a)w(b)w(c)$
of
$w(a)w(b)w(c)$
of
![]() $w(1)w(2)\cdots w(n)$
for
$w(1)w(2)\cdots w(n)$
for
![]() $1\leq a< b< c\leq n$
has the form
$1\leq a< b< c\leq n$
has the form
![]() $(i-1)i(i+1)$
for any integer
$(i-1)i(i+1)$
for any integer
![]() $1< i< n$
.
$1< i< n$
.
Fix
![]() $z \in \mathcal {I}_n$
. The involution code of
$z \in \mathcal {I}_n$
. The involution code of
![]() $z $
is
$z $
is
![]() $\hat c(z) = (\hat c_1(z),\hat c_2(z),\dots ,\hat c_n(z))$
with
$\hat c(z) = (\hat c_1(z),\hat c_2(z),\dots ,\hat c_n(z))$
with
![]() $\hat c_i(z)$
the number of integers
$\hat c_i(z)$
the number of integers
![]() $j>i$
with
$j>i$
with
![]() $z(i)> z(j)$
and
$z(i)> z(j)$
and
![]() $i\geq z(j)$
. Note that we always have
$i\geq z(j)$
. Note that we always have
![]() $\hat c_i(z) \leq i$
.
$\hat c_i(z) \leq i$
.
Suppose
![]() $a_1< a_2< \dots < a_l$
are the integers
$a_1< a_2< \dots < a_l$
are the integers
![]() $a\in [n]$
with
$a\in [n]$
with
![]() $a \leq z(a)$
and set
$a \leq z(a)$
and set
![]() $b_i = z(a_i)$
. Define
$b_i = z(a_i)$
. Define
![]() $\alpha _{\min }(z) \in S_n$
to be the permutation whose inverse is given in one-line notation by removing all repeated letters from
$\alpha _{\min }(z) \in S_n$
to be the permutation whose inverse is given in one-line notation by removing all repeated letters from
![]() $b_1 a_1 b_2 a_2\cdots b_l a_l$
. For example, if
$b_1 a_1 b_2 a_2\cdots b_l a_l$
. For example, if
![]() $z = 4231 \in \mathcal {I}_4$
then the latter word is
$z = 4231 \in \mathcal {I}_4$
then the latter word is
![]() $412233$
and
$412233$
and
![]() $\alpha _{\min }(z) = (4123)^{-1} = 2341 \in S_4$
. Additionally,
$\alpha _{\min }(z) = (4123)^{-1} = 2341 \in S_4$
. Additionally,
![]() $\hat c(z) = c(\alpha _{\min }(z))$
[Reference Hamaker, Marberg and Pawlowski13, Lemma 3.8].
$\hat c(z) = c(\alpha _{\min }(z))$
[Reference Hamaker, Marberg and Pawlowski13, Lemma 3.8].
Finally, let
![]() $\prec _{\mathcal {A}}$
be the transitive closure of the relation on
$\prec _{\mathcal {A}}$
be the transitive closure of the relation on
![]() $S_n$
that has
$S_n$
that has
![]() $v \prec _{\mathcal {A}} w$
whenever the inverses of
$v \prec _{\mathcal {A}} w$
whenever the inverses of
![]() $v,w \in S_n$
have the same one-line representations outside of three consecutive positions where
$v,w \in S_n$
have the same one-line representations outside of three consecutive positions where
![]() $v^{-1} = \cdots cab\cdots $
and
$v^{-1} = \cdots cab\cdots $
and
![]() $ w^{-1}=\cdots bca\cdots $
for some integers
$ w^{-1}=\cdots bca\cdots $
for some integers
![]() $a< b< c$
. The relation
$a< b< c$
. The relation
![]() $\prec _{\mathcal {A}}$
is a strict partial order. Let
$\prec _{\mathcal {A}}$
is a strict partial order. Let
![]() $\sim _{\mathcal {A}}$
denote the symmetric closure of the partial order
$\sim _{\mathcal {A}}$
denote the symmetric closure of the partial order
![]() $\preceq _{\mathcal {A}}$
.
$\preceq _{\mathcal {A}}$
.
Theorem 5.5 ([Reference Hamaker, Marberg and Pawlowski12, Section 6.1])
Let
![]() $z \in \mathcal {I}_n$
. Then
$z \in \mathcal {I}_n$
. Then
Thus
![]() $\mathcal {A}(z)$
is an upper and lower set of
$\mathcal {A}(z)$
is an upper and lower set of
![]() $\preceq _{\mathcal {A}}$
, with unique minimum
$\preceq _{\mathcal {A}}$
, with unique minimum
![]() $\alpha _{\min }(z)$
.
$\alpha _{\min }(z)$
.
For
![]() $z \in \mathcal {I}_n$
let
$z \in \mathcal {I}_n$
let
so that
![]() .
.
Lemma 5.6 Let
![]() $z \in \mathcal {I}_n$
. Suppose D and E are subsets of
$z \in \mathcal {I}_n$
. Suppose D and E are subsets of
![]() $\mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
with
$\mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
with
![]() $D <_{\mathcal {ID}} E $
. Then
$D <_{\mathcal {ID}} E $
. Then
![]() $D \in \mathcal {ID}^+(z)$
if and only if
$D \in \mathcal {ID}^+(z)$
if and only if
![]() $E \in \mathcal {ID}^+(z)$
.
$E \in \mathcal {ID}^+(z)$
.
Proof If
![]() $D \lessdot _{\mathcal {PD}} E$
then we have
$D \lessdot _{\mathcal {PD}} E$
then we have
![]() $D \in \mathcal {ID}^+(z)$
if and only if
$D \in \mathcal {ID}^+(z)$
if and only if
![]() $E \in \mathcal {ID}^+(z)$
by Theorem 5.2. Assume
$E \in \mathcal {ID}^+(z)$
by Theorem 5.2. Assume
![]() $D \lessdot _{\mathcal {ID}}E$
and let
$D \lessdot _{\mathcal {ID}}E$
and let
![]() $i< j$
and k be as in Definition 5.3.
$i< j$
and k be as in Definition 5.3.
Consider the reading order
![]() $\omega $
that lists the positions
$\omega $
that lists the positions
![]() $(i,j)\in [n]\times [n]$
such that
$(i,j)\in [n]\times [n]$
such that
![]() $(-j,i)$
increases lexicographically, i.e., the order that goes down column n, then down column
$(-j,i)$
increases lexicographically, i.e., the order that goes down column n, then down column
![]() $n-1$
, and so on. In view of Theorem 3.9, we may assume without loss of generality that columns
$n-1$
, and so on. In view of Theorem 3.9, we may assume without loss of generality that columns
![]() $1,2,\dots ,k-1$
of D and E are both empty, since omitting these positions has the effect of truncating the same final sequence of letters from
$1,2,\dots ,k-1$
of D and E are both empty, since omitting these positions has the effect of truncating the same final sequence of letters from
![]() $\mathsf {word}(D,\omega )$
and
$\mathsf {word}(D,\omega )$
and
![]() $\mathsf {word}(E,\omega )$
.
$\mathsf {word}(E,\omega )$
.
Suppose
![]() $E \in \mathcal {PD}(w)\subseteq \mathcal {ID}^+(z)$
for some permutation
$E \in \mathcal {PD}(w)\subseteq \mathcal {ID}^+(z)$
for some permutation
![]() $w \in \mathcal {A}(z)$
. To show that
$w \in \mathcal {A}(z)$
. To show that
![]() $D \in \mathcal {ID}^+(z)$
, it suffices by Theorem 5.5 to check that
$D \in \mathcal {ID}^+(z)$
, it suffices by Theorem 5.5 to check that
![]() $D \in \mathcal {PD}(v)$
for a permutation
$D \in \mathcal {PD}(v)$
for a permutation
![]() $v \prec _{\mathcal {A}} w$
.
$v \prec _{\mathcal {A}} w$
.
Consider the wiring diagram of E and let
![]() $m,m+1$
and
$m,m+1$
and
![]() $m+2$
be the top indices of the wires in the antidiagonals containing the cells
$m+2$
be the top indices of the wires in the antidiagonals containing the cells
![]() $ (i,k), (i,k+1)$
, and
$ (i,k), (i,k+1)$
, and
![]() $(i+1,k+1) $
, respectively. Since the northeast parts of these antidiagonals are empty, it follows that as one goes from northeast to southwest, wire m of E enters the top of the
$(i+1,k+1) $
, respectively. Since the northeast parts of these antidiagonals are empty, it follows that as one goes from northeast to southwest, wire m of E enters the top of the
![]() $+$
in cell
$+$
in cell
![]() $(i,k)$
, wire
$(i,k)$
, wire
![]() $m+1$
enters the top of the
$m+1$
enters the top of the
![]() $+$
in cell
$+$
in cell
![]() $(i,k+1)$
, and wire
$(i,k+1)$
, and wire
![]() $m+2$
enters the right of the
$m+2$
enters the right of the
![]() $+$
in cell
$+$
in cell
![]() $(i,k+1)$
. Tracing these wires through the wiring diagram of E, we see that they exit column k on the left in relative order
$(i,k+1)$
. Tracing these wires through the wiring diagram of E, we see that they exit column k on the left in relative order
![]() $m+2,m,m+1$
. Since we assume columns
$m+2,m,m+1$
. Since we assume columns
![]() $1,2,\dots ,k-1$
are empty, the wires must arrive at the far left in the same relative order. This means that there are numbers
$1,2,\dots ,k-1$
are empty, the wires must arrive at the far left in the same relative order. This means that there are numbers
![]() $a< b< c$
such that
$a< b< c$
such that
![]() $w^{-1}(m)w^{-1}(m+1)w^{-1}(m+2)=bca$
.
$w^{-1}(m)w^{-1}(m+1)w^{-1}(m+2)=bca$
.
Moving the
![]() $+$
in cell
$+$
in cell
![]() $(i,k+1)$
of E to
$(i,k+1)$
of E to
![]() $(j,k)$
gives D by assumption. This transformation only alters the trajectories of wires m,
$(j,k)$
gives D by assumption. This transformation only alters the trajectories of wires m,
![]() $m+1$
, and
$m+1$
, and
![]() $m+2$
, and causes no pair of wires to cross more than once, so D is a reduced pipe dream for some
$m+2$
, and causes no pair of wires to cross more than once, so D is a reduced pipe dream for some
![]() $v \in S_n$
. By examining the wiring diagram of D, we see that
$v \in S_n$
. By examining the wiring diagram of D, we see that
![]() $v^{-1}(m)v^{-1}(m+1)v^{-1}(m+2)=cab$
, so
$v^{-1}(m)v^{-1}(m+1)v^{-1}(m+2)=cab$
, so
![]() $v \prec _{\mathcal {A}} w$
and
$v \prec _{\mathcal {A}} w$
and
![]() $D \in \mathcal {ID}^+(z)$
as needed. The same considerations show that if
$D \in \mathcal {ID}^+(z)$
as needed. The same considerations show that if
![]() $D \in \mathcal {PD}(v)$
for some
$D \in \mathcal {PD}(v)$
for some
![]() $v \in \mathcal {A}(z)$
then
$v \in \mathcal {A}(z)$
then
![]() $E \in \mathcal {PD}(w)$
for a permutation w with
$E \in \mathcal {PD}(w)$
for a permutation w with
![]() $v \prec _{\mathcal {A}} w$
. In this case, it follows that
$v \prec _{\mathcal {A}} w$
. In this case, it follows that
![]() $w \in \mathcal {A}(z)$
by Theorem 5.5 so
$w \in \mathcal {A}(z)$
by Theorem 5.5 so
![]() $E \in \mathcal {ID}^+(z)$
.▪
$E \in \mathcal {ID}^+(z)$
.▪
We define the bottom involution pipe dream of
![]() $z \in \mathcal {I}_n$
to be the set
$z \in \mathcal {I}_n$
to be the set
Since
![]() $\hat c(z) = c(\alpha _{\min }(z))$
, Theorem 3.9 implies that
$\hat c(z) = c(\alpha _{\min }(z))$
, Theorem 3.9 implies that
![]() $\hat D_{\text {bot}}(z) = D_{\text {bot}}(\alpha _{\min }(z))\in \mathcal {ID}(z).$
$\hat D_{\text {bot}}(z) = D_{\text {bot}}(\alpha _{\min }(z))\in \mathcal {ID}(z).$
Theorem 5.7 Let
![]() $z \in \mathcal {I}_n$
. Then
$z \in \mathcal {I}_n$
. Then
Thus
![]() $\mathcal {ID}^+(z)$
is an upper and lower set of
$\mathcal {ID}^+(z)$
is an upper and lower set of
![]() $\leq _{\mathcal {ID}}$
, with unique minimum
$\leq _{\mathcal {ID}}$
, with unique minimum
![]() $\hat D_{\text {bot}}(z)$
.
$\hat D_{\text {bot}}(z)$
.
Proof Both sets are contained in
![]() $\mathcal {ID}^+(z)$
by Lemma 5.6. Note that
$\mathcal {ID}^+(z)$
by Lemma 5.6. Note that
![]() $\mathcal {ID}^+(z)$
is finite since
$\mathcal {ID}^+(z)$
is finite since
![]() $\mathcal {A}(z)$
is finite and each set
$\mathcal {A}(z)$
is finite and each set
![]() $\mathcal {PD}(w)$
is finite. Suppose
$\mathcal {PD}(w)$
is finite. Suppose
![]() $ \hat D_{\text {bot}}(z) \neq E = D_{\text {bot}}(w)$
for some
$ \hat D_{\text {bot}}(z) \neq E = D_{\text {bot}}(w)$
for some
![]() $w \in \mathcal {A}(z)$
. In view of Theorem 5.2, we need only show that there exists a subset
$w \in \mathcal {A}(z)$
. In view of Theorem 5.2, we need only show that there exists a subset
![]() $D\subset \mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
with
$D\subset \mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
with
![]() $D\lessdot _{\mathcal {ID}} E$
.
$D\lessdot _{\mathcal {ID}} E$
.
As we assume
![]() $w \neq \alpha _{\min }(z)$
, it follows from Theorem 5.5 that there exists some
$w \neq \alpha _{\min }(z)$
, it follows from Theorem 5.5 that there exists some
![]() $p \in [n-2]$
with
$p \in [n-2]$
with
![]() $w^{-1}(p{+}2) < w^{-1}(p) < w^{-1}(p{+}1)$
. Set
$w^{-1}(p{+}2) < w^{-1}(p) < w^{-1}(p{+}1)$
. Set
![]() $i = w^{-1}(p{+}2)$
, and choose p to minimize i. We claim that if
$i = w^{-1}(p{+}2)$
, and choose p to minimize i. We claim that if
![]() $h < i$
then
$h < i$
then
![]() $w(h) < p$
. To show this, we argue by contradiction. Suppose there exists
$w(h) < p$
. To show this, we argue by contradiction. Suppose there exists
![]() $1\leq h < i$
with
$1\leq h < i$
with
![]() $w(h) \geq p$
. Choose h with this property so that
$w(h) \geq p$
. Choose h with this property so that
![]() $w(h)$
is as small as possible. Then
$w(h)$
is as small as possible. Then
![]() $w(h)> p+2 \geq 3$
, and by the minimality of
$w(h)> p+2 \geq 3$
, and by the minimality of
![]() $w(h)$
, the values
$w(h)$
, the values
![]() $w(h){-}1$
and
$w(h){-}1$
and
![]() $w(h){-}2$
appear after position h in the word
$w(h){-}2$
appear after position h in the word
![]() $w(1)w(2)\cdots w(n)$
. Therefore, by Lemma 5.4, the one-line representation of w must have the form
$w(1)w(2)\cdots w(n)$
. Therefore, by Lemma 5.4, the one-line representation of w must have the form
![]() $\cdots w(h) \cdots w(h){-}2\cdots w(h){-}1\cdots $
. This contradicts the minimality of i, so no such h can exist.
$\cdots w(h) \cdots w(h){-}2\cdots w(h){-}1\cdots $
. This contradicts the minimality of i, so no such h can exist.
Let
![]() $j> i$
be minimal with
$j> i$
be minimal with
![]() $w(j) < w(i)$
and define
$w(j) < w(i)$
and define
![]() $k = c_i(w) - 1$
. It is evident from the definition of i that such an index j exists and that k is positive. Now consider Definition 5.3 applied to these values of
$k = c_i(w) - 1$
. It is evident from the definition of i that such an index j exists and that k is positive. Now consider Definition 5.3 applied to these values of
![]() $i< j$
and k. It follows from the claim in the previous paragraph if
$i< j$
and k. It follows from the claim in the previous paragraph if
![]() $h< i$
then
$h< i$
then
![]() $c_h(w) - c_i(w) \leq i-h -3$
. Therefore, we see that the required antidiagonals are empty. The minimality of j implies that
$c_h(w) - c_i(w) \leq i-h -3$
. Therefore, we see that the required antidiagonals are empty. The minimality of j implies that
![]() $c_m(w) \geq c_i(w)$
for all
$c_m(w) \geq c_i(w)$
for all
![]() $i < m < j$
, and since we must have
$i < m < j$
, and since we must have
![]() $j \leq w^{-1}(p)$
, it follows that
$j \leq w^{-1}(p)$
, it follows that
![]() $c_j(w) < c_i(w) - 1$
. We conclude that replacing position
$c_j(w) < c_i(w) - 1$
. We conclude that replacing position
![]() $(i,k+1)$
in E by
$(i,k+1)$
in E by
![]() $(j,k)$
produces a subset D with
$(j,k)$
produces a subset D with
![]() $D \lessdot _{\mathcal {ID}} E$
, as we needed to show.▪
$D \lessdot _{\mathcal {ID}} E$
, as we needed to show.▪
Theorem 5.8 If
![]() $z \in \mathcal {I}_n$
then
$z \in \mathcal {I}_n$
then
Proof This is clear from Theorem 5.7 since
![]() is a lower set under
is a lower set under
![]() $\leq _{\mathcal {ID}}$
.▪
$\leq _{\mathcal {ID}}$
.▪
5.3 Fixed-point-free involution ladder moves
In this subsection, we assume n is a positive even integer. Our goal is to replicate the results in Section 5.2 for fixed-point-free involutions. To this end, we introduce a third partial order
![]() $<_{\mathcal {FD}}$
. Again let D and E be subsets of
$<_{\mathcal {FD}}$
. Again let D and E be subsets of
![]() $\mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
. We define
$\mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
. We define
![]() $<_{\mathcal {FD}}$
as the transitive closure of
$<_{\mathcal {FD}}$
as the transitive closure of
![]() $\lessdot _{\mathcal {PD}}$
and the relation that has
$\lessdot _{\mathcal {PD}}$
and the relation that has
![]() $D \lessdot _{\mathcal {FD}} E$
whenever E is obtained from
$D \lessdot _{\mathcal {FD}} E$
whenever E is obtained from
![]() $D $
by replacing a subset of the form
$D $
by replacing a subset of the form
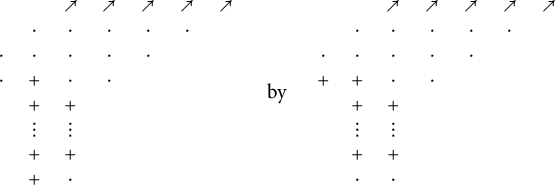 $$ \begin{align} \begin{array}{ccccccc} {\phantom+} & {\phantom+} & \nearrow & \nearrow & \nearrow & \nearrow & \nearrow \\ {\phantom+} & \cdot & \cdot & \cdot &\cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot\\ \cdot & + & \cdot & \cdot\\ & + & + \\ & \vdots & \vdots \\ & + & + \\ & + & \cdot & {\phantom+} & {\phantom+} & {\phantom+}& {\phantom+} \end{array} \quad\text{by}\quad \begin{array}{ccccccc} {\phantom+} & {\phantom+} & \nearrow & \nearrow & \nearrow & \nearrow & \nearrow \\ {\phantom+} & \cdot & \cdot & \cdot &\cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot\\ + & + & \cdot & \cdot\\ & + & + \\ & \vdots & \vdots \\ & + & + \\ & \cdot & \cdot & {\phantom+} & {\phantom+} & {\phantom+}& {\phantom+} \end{array} \end{align} $$
$$ \begin{align} \begin{array}{ccccccc} {\phantom+} & {\phantom+} & \nearrow & \nearrow & \nearrow & \nearrow & \nearrow \\ {\phantom+} & \cdot & \cdot & \cdot &\cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot\\ \cdot & + & \cdot & \cdot\\ & + & + \\ & \vdots & \vdots \\ & + & + \\ & + & \cdot & {\phantom+} & {\phantom+} & {\phantom+}& {\phantom+} \end{array} \quad\text{by}\quad \begin{array}{ccccccc} {\phantom+} & {\phantom+} & \nearrow & \nearrow & \nearrow & \nearrow & \nearrow \\ {\phantom+} & \cdot & \cdot & \cdot &\cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot\\ + & + & \cdot & \cdot\\ & + & + \\ & \vdots & \vdots \\ & + & + \\ & \cdot & \cdot & {\phantom+} & {\phantom+} & {\phantom+}& {\phantom+} \end{array} \end{align} $$
Here, all positions containing “
![]() $\;\cdot\; $
” should be empty, including the five antidiagonals extending upwards beyond each
$\;\cdot\; $
” should be empty, including the five antidiagonals extending upwards beyond each
![]() $\nearrow $
. For example,
$\nearrow $
. For example,
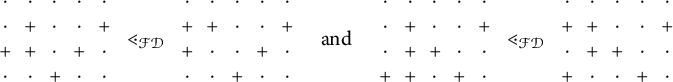 $$ \begin{align*} \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot & \cdot\\ \cdot & + & \cdot & \cdot & +\\ + & + & \cdot & +& \cdot\\ \cdot & \cdot& + & \cdot & \cdot \end{array} \ \lessdot_{\mathcal{FD}}\ \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot & \cdot\\ + & + & \cdot & \cdot & +\\ + & \cdot & \cdot & +& \cdot\\ \cdot & \cdot & + & \cdot & \cdot \end{array} \quad\text{and}\quad \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot & \cdot\\ \cdot & + & \cdot & \cdot & +\\ \cdot & + & + & \cdot& \cdot\\ + & + & \cdot & + & \cdot \end{array} \ \lessdot_{\mathcal{FD}}\ \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot & \cdot\\ + & + & \cdot & \cdot & +\\ \cdot & + & + & \cdot& \cdot\\ + & \cdot & \cdot & + & \cdot \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot & \cdot\\ \cdot & + & \cdot & \cdot & +\\ + & + & \cdot & +& \cdot\\ \cdot & \cdot& + & \cdot & \cdot \end{array} \ \lessdot_{\mathcal{FD}}\ \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot & \cdot\\ + & + & \cdot & \cdot & +\\ + & \cdot & \cdot & +& \cdot\\ \cdot & \cdot & + & \cdot & \cdot \end{array} \quad\text{and}\quad \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot & \cdot\\ \cdot & + & \cdot & \cdot & +\\ \cdot & + & + & \cdot& \cdot\\ + & + & \cdot & + & \cdot \end{array} \ \lessdot_{\mathcal{FD}}\ \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot & \cdot\\ + & + & \cdot & \cdot & +\\ \cdot & + & + & \cdot& \cdot\\ + & \cdot & \cdot & + & \cdot \end{array} \end{align*} $$
but
 $$ \begin{align*} \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot & +\\ \cdot & + & \cdot & \cdot & \cdot\\ \cdot & + & \cdot & +& \cdot\\ \cdot & \cdot& + & \cdot & \cdot \end{array} \ \nless _{\mathcal{FD}}\ \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot & +\\ + & + & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & +& \cdot\\ \cdot & \cdot & + & \cdot & \cdot \end{array} \quad\text{and}\quad \begin{array}{cccccc} + & \cdot & \cdot & \cdot & \cdot\\ \cdot & + & \cdot & \cdot & +\\ \cdot & + & + & \cdot& \cdot\\ \cdot & + & \cdot & + & \cdot \end{array} \ \nless _{\mathcal{FD}}\ \begin{array}{cccccc} + & \cdot & \cdot & \cdot & \cdot\\ + & + & \cdot & \cdot & +\\ \cdot & + & + & \cdot& \cdot\\ \cdot & \cdot & \cdot & + & \cdot \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot & +\\ \cdot & + & \cdot & \cdot & \cdot\\ \cdot & + & \cdot & +& \cdot\\ \cdot & \cdot& + & \cdot & \cdot \end{array} \ \nless _{\mathcal{FD}}\ \begin{array}{cccccc} \cdot & \cdot & \cdot & \cdot & +\\ + & + & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & +& \cdot\\ \cdot & \cdot & + & \cdot & \cdot \end{array} \quad\text{and}\quad \begin{array}{cccccc} + & \cdot & \cdot & \cdot & \cdot\\ \cdot & + & \cdot & \cdot & +\\ \cdot & + & + & \cdot& \cdot\\ \cdot & + & \cdot & + & \cdot \end{array} \ \nless _{\mathcal{FD}}\ \begin{array}{cccccc} + & \cdot & \cdot & \cdot & \cdot\\ + & + & \cdot & \cdot & +\\ \cdot & + & + & \cdot& \cdot\\ \cdot & \cdot & \cdot & + & \cdot \end{array} \end{align*} $$
since the relevant antidiagonals in (5.3) are not empty. The precise definition of
![]() $\lessdot _{\mathcal {FD}}$
is:
$\lessdot _{\mathcal {FD}}$
is:
Definition 5.9 We write
![]() $ D \lessdot _{\mathcal {FD}} E$
if for some integers
$ D \lessdot _{\mathcal {FD}} E$
if for some integers
![]() $0< i< j$
and
$0< i< j$
and
![]() $k\geq 2$
the following holds:
$k\geq 2$
the following holds:
-
• One has
 $\{i+1,i+2,\dots ,j-1\}\times \{k,k+1\} \subset D$
.
$\{i+1,i+2,\dots ,j-1\}\times \{k,k+1\} \subset D$
. -
• It holds that
 $(i,k),(j,k) \in D$
but
$(i,k),(j,k) \in D$
but
 $(i,k-1),(i,k+1),(i,k+2),(j,k+1)\notin D$
.
$(i,k-1),(i,k+1),(i,k+2),(j,k+1)\notin D$
. -
• One has
 $E = D\setminus \{(j,k)\} \cup \{(i,k-1)\}$
.
$E = D\setminus \{(j,k)\} \cup \{(i,k-1)\}$
. -
• The set D contains no positions strictly northeast of and in the same antidiagonal as
 $(i,k-2)$
,
$(i,k-2)$
,
 $(i,k-1)$
,
$(i,k-1)$
,
 $(i,k)$
,
$(i,k)$
,
 $(i,k+1)$
, or
$(i,k+1)$
, or
 $(i,k+2)$
.
$(i,k+2)$
.
When
![]() $i+1=j$
, the first condition holds vacuously; see the lower dashed arrow in Figure 2. Define
$i+1=j$
, the first condition holds vacuously; see the lower dashed arrow in Figure 2. Define
![]() $<_{\mathcal {FD}}$
to be the transitive closure of
$<_{\mathcal {FD}}$
to be the transitive closure of
![]() $\lessdot _{\mathcal {PD}}$
and
$\lessdot _{\mathcal {PD}}$
and
![]() $\lessdot _{\mathcal {FD}}$
. Write
$\lessdot _{\mathcal {FD}}$
. Write
![]() $\sim _{\mathcal {FD}}$
for the symmetric closure of
$\sim _{\mathcal {FD}}$
for the symmetric closure of
![]() $\leq _{\mathcal {FD}}$
.
$\leq _{\mathcal {FD}}$
.
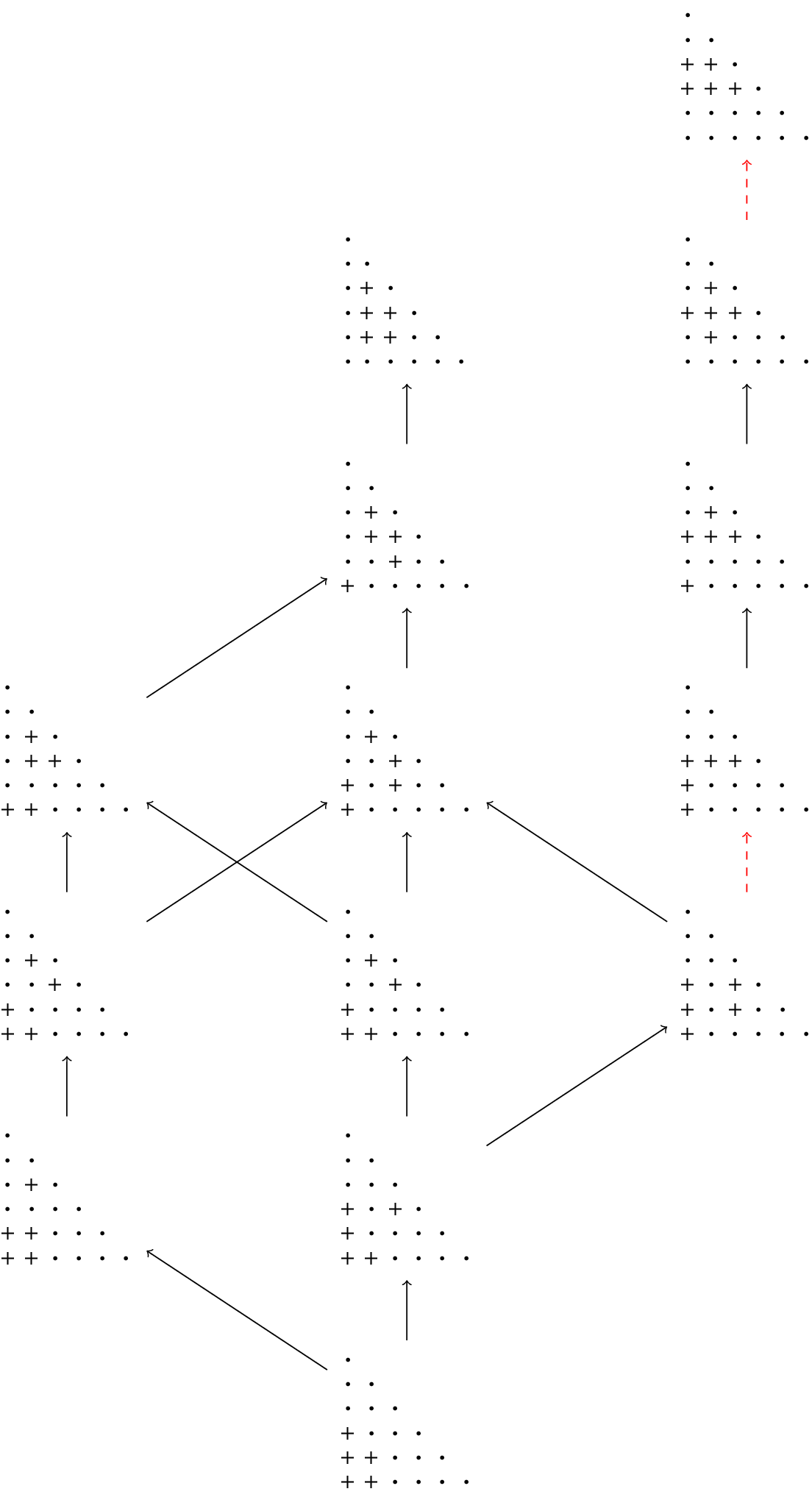
Figure 2: Hasse diagram of
![]() $(\mathcal {FD}(z), <_{\mathcal {FD}})$
for
$(\mathcal {FD}(z), <_{\mathcal {FD}})$
for
![]() $z=(1,2)(3,7)(4,8)(5,6) \in \mathcal {I}^{\mathsf {{FPF}}}_6$
. The dashed red arrows indicate the covering relations of the form
$z=(1,2)(3,7)(4,8)(5,6) \in \mathcal {I}^{\mathsf {{FPF}}}_6$
. The dashed red arrows indicate the covering relations of the form
![]() $D \lessdot _{\mathcal {FD}} E$
.
$D \lessdot _{\mathcal {FD}} E$
.
We will soon show that
![]() $<_{\mathcal {FD}}$
defines a partial order on
$<_{\mathcal {FD}}$
defines a partial order on
![]() $\mathcal {FD}(z)$
, as one can see in the example in Figure 2. For this, we will need a lemma from [Reference Can, Joyce and Wyser5] concerning
$\mathcal {FD}(z)$
, as one can see in the example in Figure 2. For this, we will need a lemma from [Reference Can, Joyce and Wyser5] concerning
![]() $\mathcal {A}^{\mathsf {{FPF}}}(z)$
.
$\mathcal {A}^{\mathsf {{FPF}}}(z)$
.
Lemma 5.10 ([Reference Can, Joyce and Wyser5, Corollary 2.16])
Let
![]() $w \in S_{n}$
and
$w \in S_{n}$
and
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_{n}$
. Then
$z \in \mathcal {I}^{\mathsf {{FPF}}}_{n}$
. Then
![]() $w \in \mathcal {A}^{\mathsf {{FPF}}}(z)$
if and only if for all
$w \in \mathcal {A}^{\mathsf {{FPF}}}(z)$
if and only if for all
![]() $a,b,c,d \in [n]$
with
$a,b,c,d \in [n]$
with
![]() $a< b=z(a)$
and
$a< b=z(a)$
and
![]() $c< d=z(c)$
, the following holds:
$c< d=z(c)$
, the following holds:
-
(1) One has
 $w(a) = 2i-1$
and
$w(a) = 2i-1$
and
 $w(b) = 2i$
for some
$w(b) = 2i$
for some
 $i \in [n/2]$
.
$i \in [n/2]$
. -
(2) If
 $a< c$
and
$a< c$
and
 $b < d$
, then
$b < d$
, then
 $w(b) < w(c)$
.
$w(b) < w(c)$
.
The involution code and partial order
![]() $\prec _{\mathcal {A}}$
both have fixed-point-free versions. Fix
$\prec _{\mathcal {A}}$
both have fixed-point-free versions. Fix
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
. The fpf-involution code of z is the integer sequence
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
. The fpf-involution code of z is the integer sequence
where
![]() $\hat c^{\mathsf {{FPF}}}_i(z)$
is the number of integers
$\hat c^{\mathsf {{FPF}}}_i(z)$
is the number of integers
![]() $j> i$
with
$j> i$
with
![]() $z(i)> z(j)$
and
$z(i)> z(j)$
and
![]() $i> z(j)$
. It always holds that
$i> z(j)$
. It always holds that
![]() $\hat c^{\mathsf {{FPF}}}_i(z) < i$
. If
$\hat c^{\mathsf {{FPF}}}_i(z) < i$
. If
![]() $a_1< a_2< \dots < a_{n/2}$
are the numbers
$a_1< a_2< \dots < a_{n/2}$
are the numbers
![]() $a\in [n]$
with
$a\in [n]$
with
![]() $a< z(a)$
and
$a< z(a)$
and
![]() $b_i = z(a_i)$
, then let
$b_i = z(a_i)$
, then let
For example, if
![]() $z = 632541 \in \mathcal {I}^{\mathsf {{FPF}}}_6$
then we have
$z = 632541 \in \mathcal {I}^{\mathsf {{FPF}}}_6$
then we have
![]() $\alpha ^{\mathsf {{FPF}}}_{\min }(z) = (162345)^{-1} = 134562 \in S_6$
. One can check that
$\alpha ^{\mathsf {{FPF}}}_{\min }(z) = (162345)^{-1} = 134562 \in S_6$
. One can check that
![]() $\hat c^{\mathsf {{FPF}}}(z) = c(\alpha ^{\mathsf {{FPF}}}_{\min }(z))$
[Reference Hamaker, Marberg and Pawlowski13, Lemma 3.8].
$\hat c^{\mathsf {{FPF}}}(z) = c(\alpha ^{\mathsf {{FPF}}}_{\min }(z))$
[Reference Hamaker, Marberg and Pawlowski13, Lemma 3.8].
Define
![]() $\prec _{\mathcal {A}^{\mathsf {{FPF}}}}$
to be the transitive closure of the relation in
$\prec _{\mathcal {A}^{\mathsf {{FPF}}}}$
to be the transitive closure of the relation in
![]() $S_n$
that has
$S_n$
that has
![]() $v \prec _{\mathcal {A}^{\mathsf {{FPF}}}} w$
whenever the inverses of
$v \prec _{\mathcal {A}^{\mathsf {{FPF}}}} w$
whenever the inverses of
![]() $v,w \in S_n$
have the same one-line representations outside of four consecutive positions where
$v,w \in S_n$
have the same one-line representations outside of four consecutive positions where
![]() $v^{-1} = \cdots adbc \cdots $
and
$v^{-1} = \cdots adbc \cdots $
and
![]() $w^{-1} = \cdots bcad \cdots $
for some integers
$w^{-1} = \cdots bcad \cdots $
for some integers
![]() $a< b< c< d$
. This is a strict partial order on
$a< b< c< d$
. This is a strict partial order on
![]() $S_n$
. Let
$S_n$
. Let
![]() $\sim _{\mathcal {A}^{\mathsf {{FPF}}}}$
denote the symmetric closure of the partial order
$\sim _{\mathcal {A}^{\mathsf {{FPF}}}}$
denote the symmetric closure of the partial order
![]() $\preceq _{\mathcal {A}^{\mathsf {{FPF}}}}$
.
$\preceq _{\mathcal {A}^{\mathsf {{FPF}}}}$
.
Theorem 5.11 ([Reference Hamaker, Marberg and Pawlowski12, Section 6.2])
Let
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
. Then
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
. Then
Thus
![]() $\mathcal {A}^{\mathsf {{FPF}}}(z)$
is an upper and lower set of
$\mathcal {A}^{\mathsf {{FPF}}}(z)$
is an upper and lower set of
![]() $\preceq _{\mathcal {A}^{\mathsf {{FPF}}}}$
, with unique minimum
$\preceq _{\mathcal {A}^{\mathsf {{FPF}}}}$
, with unique minimum
![]() $\alpha ^{\mathsf {{FPF}}}_{\min }(z)$
.
$\alpha ^{\mathsf {{FPF}}}_{\min }(z)$
.
For
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
, let
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
, let
![]() $\mathcal {FD}^+(z) = \bigsqcup _{w\in \mathcal {A}^{\mathsf {{FPF}}}(z)} \mathcal {PD}(w)$
, so
$\mathcal {FD}^+(z) = \bigsqcup _{w\in \mathcal {A}^{\mathsf {{FPF}}}(z)} \mathcal {PD}(w)$
, so
![]() .
.
Lemma 5.12 Let
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
. Suppose D and E are subsets of
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
. Suppose D and E are subsets of
![]() $\mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
with
$\mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
with
![]() $D <_{\mathcal {FD}} E $
. Then
$D <_{\mathcal {FD}} E $
. Then
![]() $D \in \mathcal {FD}^+(z)$
if and only if
$D \in \mathcal {FD}^+(z)$
if and only if
![]() $E \in \mathcal {FD}^+(z)$
.
$E \in \mathcal {FD}^+(z)$
.
Proof If
![]() $D \lessdot _{\mathcal {PD}} E$
then the result follows by Theorem 5.2. Assume
$D \lessdot _{\mathcal {PD}} E$
then the result follows by Theorem 5.2. Assume
![]() $D \lessdot _{\mathcal {FD}}E$
and let
$D \lessdot _{\mathcal {FD}}E$
and let
![]() $i< j$
and k be as in Definition 5.9.
$i< j$
and k be as in Definition 5.9.
As in the proof of Theorem 5.6, consider the reading order
![]() $\omega $
that lists the positions
$\omega $
that lists the positions
![]() $(i,j)\in [n]\times [n]$
such that
$(i,j)\in [n]\times [n]$
such that
![]() $(-j,i)$
increases lexicographically. In view of Theorem 3.12, we may assume without loss of generality that columns
$(-j,i)$
increases lexicographically. In view of Theorem 3.12, we may assume without loss of generality that columns
![]() $1,2,\dots ,k-2$
, as well as all positions below row i in column
$1,2,\dots ,k-2$
, as well as all positions below row i in column
![]() $k-1$
, are empty in both of D and E. This follows since omitting these positions has the effect of truncating the same final sequence of letters from
$k-1$
, are empty in both of D and E. This follows since omitting these positions has the effect of truncating the same final sequence of letters from
![]() $\mathsf {word}(D,\omega )$
and
$\mathsf {word}(D,\omega )$
and
![]() $\mathsf {word}(E,\omega )$
.
$\mathsf {word}(E,\omega )$
.
Assume
![]() $E \in \mathcal {PD}(v) \subseteq \mathcal {FD}^+(z)$
for some
$E \in \mathcal {PD}(v) \subseteq \mathcal {FD}^+(z)$
for some
![]() $w \in \mathcal {A}^{\mathsf {{FPF}}}(z)$
. To show that
$w \in \mathcal {A}^{\mathsf {{FPF}}}(z)$
. To show that
![]() $D \in \mathcal {FD}^+(z)$
, we will check that
$D \in \mathcal {FD}^+(z)$
, we will check that
![]() $D \in \mathcal {PD}(v)$
for some
$D \in \mathcal {PD}(v)$
for some
![]() $v\in S_n$
with
$v\in S_n$
with
![]() $v \prec _{\mathcal {A}^{\mathsf {{FPF}}}} w$
.
$v \prec _{\mathcal {A}^{\mathsf {{FPF}}}} w$
.
Consider the wiring diagram of E and let m,
![]() $m+1$
,
$m+1$
,
![]() $m+2$
, and
$m+2$
, and
![]() $m+3$
be the top indices of the wires in the antidiagonals containing the cells
$m+3$
be the top indices of the wires in the antidiagonals containing the cells
![]() $(i,k-1)$
,
$(i,k-1)$
,
![]() $(i,k)$
,
$(i,k)$
,
![]() $(i,k+1)$
, and
$(i,k+1)$
, and
![]() $(i,k+2)$
, respectively. Since the northeast parts of these antidiagonals are empty, it follows that as one goes from northeast to southwest, wire m of E enters the top of the
$(i,k+2)$
, respectively. Since the northeast parts of these antidiagonals are empty, it follows that as one goes from northeast to southwest, wire m of E enters the top of the
![]() $+$
in cell
$+$
in cell
![]() $(i,k-1)$
, wire
$(i,k-1)$
, wire
![]() $m+1$
enters the top of the
$m+1$
enters the top of the
![]() $+$
is cell
$+$
is cell
![]() $(i,k)$
, wire
$(i,k)$
, wire
![]() $m+2$
enters the right of the
$m+2$
enters the right of the
![]() $+$
in cell
$+$
in cell
![]() $(i,k)$
, and wire
$(i,k)$
, and wire
![]() $m+3$
enters the top of cell
$m+3$
enters the top of cell
![]() $(i+1,k+1)$
, which contains a
$(i+1,k+1)$
, which contains a
![]() $+$
if
$+$
if
![]() $i+1< j$
. Tracing these wires through the wiring diagram of E, we see that they exit column
$i+1< j$
. Tracing these wires through the wiring diagram of E, we see that they exit column
![]() $k-1$
on the left in relative order
$k-1$
on the left in relative order
![]() $m+2$
, m,
$m+2$
, m,
![]() $m+1$
,
$m+1$
,
![]() $m+3$
. Since we assume that D and E contain no positions in the rectangle weakly southwest of
$m+3$
. Since we assume that D and E contain no positions in the rectangle weakly southwest of
![]() $(i+1,k-1)$
, the wires must arrive at the far left in the same relative order. This means that
$(i+1,k-1)$
, the wires must arrive at the far left in the same relative order. This means that
![]() $w^{-1}(m)w^{-1}(m+1) w^{-1}(m+2) w^{-1}(m+3) = bcad$
for some numbers
$w^{-1}(m)w^{-1}(m+1) w^{-1}(m+2) w^{-1}(m+3) = bcad$
for some numbers
![]() $a< b< c< d$
.
$a< b< c< d$
.
Moving the
![]() $+$
in cell
$+$
in cell
![]() $(i,k-1)$
of E to
$(i,k-1)$
of E to
![]() $(j,k)$
gives D by assumption. This transformation only alters the trajectories of wires m,
$(j,k)$
gives D by assumption. This transformation only alters the trajectories of wires m,
![]() $m+1$
,
$m+1$
,
![]() $m+2$
, and
$m+2$
, and
![]() $m+3$
and causes no pair of wires to cross more than once, so D is a reduced pipe dream for some
$m+3$
and causes no pair of wires to cross more than once, so D is a reduced pipe dream for some
![]() $v \in S_n$
. By examining the wiring diagram of D, it is easy to check that
$v \in S_n$
. By examining the wiring diagram of D, it is easy to check that
![]() $v^{-1}(m)v^{-1}(m+1) v^{-1}(m+2) v^{-1}(m+3) = adbc$
so
$v^{-1}(m)v^{-1}(m+1) v^{-1}(m+2) v^{-1}(m+3) = adbc$
so
![]() $v \prec _{\mathcal {A}^{\mathsf {{FPF}}}} w$
as needed.
$v \prec _{\mathcal {A}^{\mathsf {{FPF}}}} w$
as needed.
If instead
![]() $D \in \mathcal {PD}(v)\subset \mathcal {FD}^+(z)$
for some
$D \in \mathcal {PD}(v)\subset \mathcal {FD}^+(z)$
for some
![]() $v \in \mathcal {A}^{\mathsf {{FPF}}}(z)$
, then a similar argument shows that
$v \in \mathcal {A}^{\mathsf {{FPF}}}(z)$
, then a similar argument shows that
![]() $E \in \mathcal {PD}(w)$
for some
$E \in \mathcal {PD}(w)$
for some
![]() $w \in S_n$
with
$w \in S_n$
with
![]() $v \prec _{\mathcal {A}^{\mathsf {{FPF}}}} w$
, which implies that
$v \prec _{\mathcal {A}^{\mathsf {{FPF}}}} w$
, which implies that
![]() $E \in \mathcal {FD}^+(z)$
by Theorem 5.11.▪
$E \in \mathcal {FD}^+(z)$
by Theorem 5.11.▪
We define the bottom fpf-involution pipe dream of
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
to be the set
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
to be the set
As
![]() $\hat c^{\mathsf {{FPF}}}(z) = c(\alpha ^{\mathsf {{FPF}}}_{\min }(z))$
, Theorem 3.12 implies
$\hat c^{\mathsf {{FPF}}}(z) = c(\alpha ^{\mathsf {{FPF}}}_{\min }(z))$
, Theorem 3.12 implies
![]() $ \hat D_{\text {bot}}^{\mathsf {{FPF}}}(z) = D_{\text {bot}}(\alpha ^{\mathsf {{FPF}}}_{\min }(z)) \in \mathcal {FD}(z). $
$ \hat D_{\text {bot}}^{\mathsf {{FPF}}}(z) = D_{\text {bot}}(\alpha ^{\mathsf {{FPF}}}_{\min }(z)) \in \mathcal {FD}(z). $
Theorem 5.13 Let
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
. Then
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
. Then
Thus
![]() $\mathcal {FD}^+(z)$
is an upper and lower set of
$\mathcal {FD}^+(z)$
is an upper and lower set of
![]() $\leq _{\mathcal {FD}}$
, with unique minimum
$\leq _{\mathcal {FD}}$
, with unique minimum
![]() $\hat D_{\text {bot}}^{\mathsf {{FPF}}}(z)$
.
$\hat D_{\text {bot}}^{\mathsf {{FPF}}}(z)$
.
Proof Both sets are contained in
![]() $\mathcal {FD}^+(z)$
by Lemma 5.12, and the set
$\mathcal {FD}^+(z)$
by Lemma 5.12, and the set
![]() $\mathcal {FD}^+(z)$
is clearly finite. Suppose
$\mathcal {FD}^+(z)$
is clearly finite. Suppose
![]() $ \hat D_{\text {bot}}^{\mathsf {{FPF}}}(z) \neq E = D_{\text {bot}}(w)$
for some
$ \hat D_{\text {bot}}^{\mathsf {{FPF}}}(z) \neq E = D_{\text {bot}}(w)$
for some
![]() $w \in \mathcal {A}^{\mathsf {{FPF}}}(z)$
. As in the proof of Theorem 5.7, it suffices to show that there exists a subset
$w \in \mathcal {A}^{\mathsf {{FPF}}}(z)$
. As in the proof of Theorem 5.7, it suffices to show that there exists a subset
![]() $D\subset \mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
with
$D\subset \mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
with
![]() $D\lessdot _{\mathcal {FD}} E$
.
$D\lessdot _{\mathcal {FD}} E$
.
Since
![]() $w \neq \alpha ^{\mathsf {{FPF}}}_{\min }(z)$
, Lemma 5.10 and Theorem 5.11 imply that there exists an odd integer
$w \neq \alpha ^{\mathsf {{FPF}}}_{\min }(z)$
, Lemma 5.10 and Theorem 5.11 imply that there exists an odd integer
![]() $p \in [n - 3]$
such that
$p \in [n - 3]$
such that
![]() $ w^{-1}(p)w^{-1}(p+1)w^{-1}(p+2)w^{-1}(p+3) = bcad$
for some numbers
$ w^{-1}(p)w^{-1}(p+1)w^{-1}(p+2)w^{-1}(p+3) = bcad$
for some numbers
![]() $a< b< c< d$
. Choose p such that a is as small as possible. We claim that
$a< b< c< d$
. Choose p such that a is as small as possible. We claim that
![]() $a< w^{-1}(q)$
for all q with
$a< w^{-1}(q)$
for all q with
![]() $p+3 < q \leq n$
. To show this, let
$p+3 < q \leq n$
. To show this, let
![]() $a_0=a$
and
$a_0=a$
and
![]() $b_0 =d$
and suppose
$b_0 =d$
and suppose
![]() $a_i $
and
$a_i $
and
![]() $b_i$
are the integers such that
$b_i$
are the integers such that
Part (1) of Lemma 5.10 implies that
![]() $a_i < b_i =z(a_i)$
for all i, so it suffices to show that
$a_i < b_i =z(a_i)$
for all i, so it suffices to show that
![]() $a_0< a_i$
for
$a_0< a_i$
for
![]() $i \in [k]$
. This holds since if
$i \in [k]$
. This holds since if
![]() $i \in [k]$
were minimal with
$i \in [k]$
were minimal with
![]() $a_i < a_0$
, then it would follow from part (2) of Lemma 5.10 that
$a_i < a_0$
, then it would follow from part (2) of Lemma 5.10 that
![]() $a_i < a_{i-1} < b_{i-1}< b_i$
, contradicting the minimality of a.
$a_i < a_{i-1} < b_{i-1}< b_i$
, contradicting the minimality of a.
Now, to match Definition 5.9, let
![]() $i = a=w^{-1}(p+2)$
, define
$i = a=w^{-1}(p+2)$
, define
![]() $j> i$
to be minimal with
$j> i$
to be minimal with
![]() $w(j) < w(i)$
, and set
$w(j) < w(i)$
, and set
![]() $k = c_i(w)$
. It is clear from the definition of i that such an index j exists and that
$k = c_i(w)$
. It is clear from the definition of i that such an index j exists and that
![]() $k\geq 2$
. The claim in the previous paragraph shows that if
$k\geq 2$
. The claim in the previous paragraph shows that if
![]() $1\leq h < i$
then h must appear before position p in the one-line representation of
$1\leq h < i$
then h must appear before position p in the one-line representation of
![]() $w^{-1}$
, which means that
$w^{-1}$
, which means that
![]() $w(h)< p$
and therefore
$w(h)< p$
and therefore
![]() $c_h(w) - c_i(w) \leq i-h- 4$
. The antidiagonals described in Definition 5.9 are thus empty as needed. Since
$c_h(w) - c_i(w) \leq i-h- 4$
. The antidiagonals described in Definition 5.9 are thus empty as needed. Since
![]() $j \leq b= w^{-1}(p)$
, it follows that
$j \leq b= w^{-1}(p)$
, it follows that
![]() $c_j(w) < c_i(w)$
; moreover, if
$c_j(w) < c_i(w)$
; moreover, if
![]() $i < m < j$
then
$i < m < j$
then
![]() $w(m)> w(d) = p+3$
so
$w(m)> w(d) = p+3$
so
![]() $c_m(w) \geq c_i(w) + 1$
. Collecting these observations, we conclude that replacing
$c_m(w) \geq c_i(w) + 1$
. Collecting these observations, we conclude that replacing
![]() $(i,k-1)$
in E with
$(i,k-1)$
in E with
![]() $(j,k)$
gives a subset D with
$(j,k)$
gives a subset D with
![]() $D \lessdot _{\mathcal {ID}} E$
, as we needed to show.▪
$D \lessdot _{\mathcal {ID}} E$
, as we needed to show.▪
Theorem 5.14 If
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
then
Proof This is clear from Theorem 5.13 since
![]() is a lower set under
is a lower set under
![]() $\leq _{\mathcal {FD}}$
.▪
$\leq _{\mathcal {FD}}$
.▪
6 Future directions
In this final section, we discuss some related identities and open problems.
6.1 Enumerating involution pipe dreams
Choose
![]() $w \in S_n$
and let
$w \in S_n$
and let
![]() $p =\ell (w)$
. Macdonald [Reference Macdonald29, (6.11)] proved that the following specialization of a Schubert polynomial gives an exact formula for the number of reduced pipe dreams for w:
$p =\ell (w)$
. Macdonald [Reference Macdonald29, (6.11)] proved that the following specialization of a Schubert polynomial gives an exact formula for the number of reduced pipe dreams for w:
 $$ \begin{align} |\mathcal{PD}(w)| = \mathfrak{S}_w(1,1,\dots,1) = \frac{1}{p!}\sum_{(a_1,a_2,\dots,a_{p}) \in \mathcal{R}(w)} a_1 a_2\cdots a_{p}. \end{align} $$
$$ \begin{align} |\mathcal{PD}(w)| = \mathfrak{S}_w(1,1,\dots,1) = \frac{1}{p!}\sum_{(a_1,a_2,\dots,a_{p}) \in \mathcal{R}(w)} a_1 a_2\cdots a_{p}. \end{align} $$
Recall that
![]() $\kappa (y)$
is the number of two-cycles in
$\kappa (y)$
is the number of two-cycles in
![]() $y \in \mathcal {I}_n$
. For
$y \in \mathcal {I}_n$
. For
![]() $D \in \mathcal {ID}(y)$
, define
$D \in \mathcal {ID}(y)$
, define
where
![]() $d_D $
is the number of diagonal positions in D. For
$d_D $
is the number of diagonal positions in D. For
![]() $\mathcal {X} \subseteq \mathcal {ID}(y)$
, define
$\mathcal {X} \subseteq \mathcal {ID}(y)$
, define
Corollary 6.1 Suppose
![]() $y \in \mathcal {I}_n$
,
$y \in \mathcal {I}_n$
,
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_{2n}$
, and
$z \in \mathcal {I}^{\mathsf {{FPF}}}_{2n}$
, and
![]() $p = \hat \ell (y) =\hat \ell ^{\mathsf {{FPF}}}(z)$
.
$p = \hat \ell (y) =\hat \ell ^{\mathsf {{FPF}}}(z)$
.
-
(a)
 $\displaystyle \|\mathcal {ID}(y)\| = 2^{\kappa (y)} \hat {\mathfrak {S}}_y(\tfrac {1}{2},\tfrac {1}{2},\dots ,\tfrac {1}{2}) = \frac {1}{2^pp!}\sum _{(a_1,a_2,\dots ,a_{p}) \in \hat {\mathcal {R}}(y)} 2^{\kappa (y)}a_1 a_2\cdots a_{p}$
.
$\displaystyle \|\mathcal {ID}(y)\| = 2^{\kappa (y)} \hat {\mathfrak {S}}_y(\tfrac {1}{2},\tfrac {1}{2},\dots ,\tfrac {1}{2}) = \frac {1}{2^pp!}\sum _{(a_1,a_2,\dots ,a_{p}) \in \hat {\mathcal {R}}(y)} 2^{\kappa (y)}a_1 a_2\cdots a_{p}$
. -
(b)
 $\displaystyle |\mathcal {FD}(z)| = \hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z(\tfrac {1}{2},\tfrac {1}{2},\dots ,\tfrac {1}{2}) = \frac {1}{2^pp!}\sum _{(a_1,a_2,\dots ,a_{p}) \in \hat {\mathcal {R}}^{\mathsf {{FPF}}}(z)} a_1 a_2\cdots a_{p}$
.
$\displaystyle |\mathcal {FD}(z)| = \hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z(\tfrac {1}{2},\tfrac {1}{2},\dots ,\tfrac {1}{2}) = \frac {1}{2^pp!}\sum _{(a_1,a_2,\dots ,a_{p}) \in \hat {\mathcal {R}}^{\mathsf {{FPF}}}(z)} a_1 a_2\cdots a_{p}$
.
Proof In both parts, the first equality is immediate from Theorem 1.5 and the second equality is a consequence of (6.1), via Definitions 2.3 and 2.6.▪
Billey et al. gave the first bijective proof of (6.1) (and of a more general q-analogue) in the recent paper [Reference Billey, Holroyd and Young2]. This follow-up problem is natural:
Problem 6.2 Find bijective proofs of the identities in Corollary 6.1.
For some permutations, better formulas than 6.1 are available. A reverse plane partition of shape
![]() $D \subset \mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
is a map
$D \subset \mathbb {Z}_{>0}\times \mathbb {Z}_{>0}$
is a map
![]() $T: D \to \mathbb {Z}_{\geq 0}$
such that
$T: D \to \mathbb {Z}_{\geq 0}$
such that
![]() $ T(i,j) \leq T(i+1,j)$
and
$ T(i,j) \leq T(i+1,j)$
and
![]() $T(i,j) \leq T(i,j+1)$
for all relevant
$T(i,j) \leq T(i,j+1)$
for all relevant
![]() $(i,j) \in D$
. If
$(i,j) \in D$
. If
![]() $\lambda $
is a partition, then let
$\lambda $
is a partition, then let
![]() $\mathsf {RPP}_\lambda (k)$
be the set of reverse plane partitions of Ferrers shape
$\mathsf {RPP}_\lambda (k)$
be the set of reverse plane partitions of Ferrers shape
![]() $\mathsf {D}_\lambda = \{ (i,j) \in \mathbb {Z}_{>0}\times \mathbb {Z}_{>0} : j \leq \lambda _i\}$
with entries in
$\mathsf {D}_\lambda = \{ (i,j) \in \mathbb {Z}_{>0}\times \mathbb {Z}_{>0} : j \leq \lambda _i\}$
with entries in
![]() $\{0,1,\dots ,k\}$
.
$\{0,1,\dots ,k\}$
.
Given
![]() $w \in S_n$
write
$w \in S_n$
write
![]() $1^k \times w$
for the permutation in
$1^k \times w$
for the permutation in
![]() $S_{n+k}$
that fixes
$S_{n+k}$
that fixes
![]() $1,2,\dots ,k$
while mapping
$1,2,\dots ,k$
while mapping
![]() $i+k \mapsto w(i) + k$
for
$i+k \mapsto w(i) + k$
for
![]() $i \in [n]$
. Fomin and Kirillov [Reference Fomin and Kirillov8, Theorem 2.1] showed that if
$i \in [n]$
. Fomin and Kirillov [Reference Fomin and Kirillov8, Theorem 2.1] showed that if
![]() $w \in S_n$
is dominant then
$w \in S_n$
is dominant then
![]() $ |\mathcal {PD}(1^k \times w)| = |\mathsf {RPP}_{\lambda }(k)| $
for the partition
$ |\mathcal {PD}(1^k \times w)| = |\mathsf {RPP}_{\lambda }(k)| $
for the partition
![]() $\lambda $
with
$\lambda $
with
![]() $\operatorname {dom}(w) = \mathsf {D}_\lambda $
. In particular:
$\operatorname {dom}(w) = \mathsf {D}_\lambda $
. In particular:
 $$ \begin{align} |\mathcal{PD}(1^k \times n \cdots 321)| = |\mathsf{RPP}_{(n-1,\dots,3,2,1)}(k)| = \prod_{1 \leq i < j \leq n} \frac{ i + j+2k -1}{i + j -1}. \end{align} $$
$$ \begin{align} |\mathcal{PD}(1^k \times n \cdots 321)| = |\mathsf{RPP}_{(n-1,\dots,3,2,1)}(k)| = \prod_{1 \leq i < j \leq n} \frac{ i + j+2k -1}{i + j -1}. \end{align} $$
Serrano and Stump gave a bijective proof of this identity in [Reference Serrano and Stump42]. There are similar formulas counting (weighted) involution pipe dreams. For example:
Proposition 6.3 Let
![]() $g_n = n{+1} \dots 2n\ 1 \dots n \in \mathcal {I}_{2n}$
. Then
$g_n = n{+1} \dots 2n\ 1 \dots n \in \mathcal {I}_{2n}$
. Then
Proof It follows from Theorem 5.5 that
![]() $\mathcal {A}(g_n) = \{w_n \}$
for
$\mathcal {A}(g_n) = \{w_n \}$
for
![]() $w_n = 246 \cdots (2n) 135 \cdots (2n-1) \in S_{2n}$
, and that
$w_n = 246 \cdots (2n) 135 \cdots (2n-1) \in S_{2n}$
, and that
![]() $\mathcal {A}(1^k\times g_n) = \{1^k \times w_n\}$
. Moreover, we have
$\mathcal {A}(1^k\times g_n) = \{1^k \times w_n\}$
. Moreover, we have
![]() $\hat D_{\text {bot}}(1^k\times g_n) = \{ (j+k,i) : 1 \leq i \leq j \leq n\}$
. From these facts, we see that
$\hat D_{\text {bot}}(1^k\times g_n) = \{ (j+k,i) : 1 \leq i \leq j \leq n\}$
. From these facts, we see that
![]() $\mathcal {ID}(1^k \times g_n)$
is connected by ordinary ladder moves that are simple in that they replace a single cell
$\mathcal {ID}(1^k \times g_n)$
is connected by ordinary ladder moves that are simple in that they replace a single cell
![]() $(i,j)$
by
$(i,j)$
by
![]() $(i-1,j+1)$
.
$(i-1,j+1)$
.
Now consider all ways of filling the cells
![]() $(i,j)\in \hat D_{\text {bot}}(1^k\times g_n)$
by numbers
$(i,j)\in \hat D_{\text {bot}}(1^k\times g_n)$
by numbers
![]() $a \in \{0,1,\dots ,\lfloor k/2\rfloor \}$
such that rows are weakly increasing and columns are weakly decreasing. The set of such fillings is obviously in bijection with
$a \in \{0,1,\dots ,\lfloor k/2\rfloor \}$
such that rows are weakly increasing and columns are weakly decreasing. The set of such fillings is obviously in bijection with
![]() $\mathsf {RPP}_{(n,\dots ,3,2,1)}(\lfloor k/2 \rfloor )$
. On the other hand, we can transform such a filling into a subset of
$\mathsf {RPP}_{(n,\dots ,3,2,1)}(\lfloor k/2 \rfloor )$
. On the other hand, we can transform such a filling into a subset of
![]() by replacing each cell
by replacing each cell
![]() $(i,j)$
filled with a by
$(i,j)$
filled with a by
![]() $(i-a,j+a)$
. It is easy to see that this operation is a bijection from our set of fillings to
$(i-a,j+a)$
. It is easy to see that this operation is a bijection from our set of fillings to
![]() $\mathcal {ID}(1^k\times g_n)$
.▪
$\mathcal {ID}(1^k\times g_n)$
.▪
Computations indicate that if
![]() $k,n \in \mathbb {Z}_{\geq 0}$
and
$k,n \in \mathbb {Z}_{\geq 0}$
and
![]() $\{p,q\}= \{\lfloor n/2 \rfloor , \lceil n/2 \rceil \}$
then
$\{p,q\}= \{\lfloor n/2 \rfloor , \lceil n/2 \rceil \}$
then
 $$ \begin{align} |\mathcal{ID}(1^k \times n \cdots 321)| = \prod_{i=1}^{p} \prod_{j=1}^{q} \frac{i+j+k-1}{i+j-1} \end{align} $$
$$ \begin{align} |\mathcal{ID}(1^k \times n \cdots 321)| = \prod_{i=1}^{p} \prod_{j=1}^{q} \frac{i+j+k-1}{i+j-1} \end{align} $$
and
 $$ \begin{align} |\mathcal{FD}(1^{\mathsf{{FPF}}}_{2k} \times 2n \cdots 321)| = \prod_{\substack{i,j \in [n], i\neq j }} \frac{i + j +2k-1}{i + j -1}. \end{align} $$
$$ \begin{align} |\mathcal{FD}(1^{\mathsf{{FPF}}}_{2k} \times 2n \cdots 321)| = \prod_{\substack{i,j \in [n], i\neq j }} \frac{i + j +2k-1}{i + j -1}. \end{align} $$
The right-hand side of (6.3) is the number of reverse plane partitions with entries at most k of shifted shape
![]() $\mathsf {SD}_\lambda = \{ (i,i+j-1) : (i,j) \in \mathsf {D}_\lambda \}$
for
$\mathsf {SD}_\lambda = \{ (i,i+j-1) : (i,j) \in \mathsf {D}_\lambda \}$
for
![]() $\lambda = (p+q-1,p+q-3, p+q-5,\dots )$
[Reference Proctor38]. Similar formulas should hold for
$\lambda = (p+q-1,p+q-3, p+q-5,\dots )$
[Reference Proctor38]. Similar formulas should hold for
![]() $\|\mathcal {ID}(1^k \times y)\|$
and
$\|\mathcal {ID}(1^k \times y)\|$
and
![]() $|\mathcal {FD}(1^{\mathsf {{FPF}}}_{2k} \times z)|$
when
$|\mathcal {FD}(1^{\mathsf {{FPF}}}_{2k} \times z)|$
when
![]() $y \in \mathcal {I}_n$
and
$y \in \mathcal {I}_n$
and
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_{2n}$
are any (fpf-)dominant involutions. We expect that one can prove such identities algebraically using the Pfaffian formulas for
$z \in \mathcal {I}^{\mathsf {{FPF}}}_{2n}$
are any (fpf-)dominant involutions. We expect that one can prove such identities algebraically using the Pfaffian formulas for
![]() $\hat {\mathfrak {S}}_y$
and
$\hat {\mathfrak {S}}_y$
and
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
in [Reference Pawlowski37, Section 5]. A more interesting open problem is the following:
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
in [Reference Pawlowski37, Section 5]. A more interesting open problem is the following:
6.2 Ideals of matrix Schubert varieties
Another open problem is to find a geometric explanation for the formulas in Theorem 1.5. Such an explanation exists in the double Schubert case, as we briefly explain.
Recall that
![]() $A_{[i][j]}$
denotes the upper-left
$A_{[i][j]}$
denotes the upper-left
![]() $i\times j$
submatrix of a matrix A. Let
$i\times j$
submatrix of a matrix A. Let
![]() $\mathcal {Z}$
be the matrix of indeterminates
$\mathcal {Z}$
be the matrix of indeterminates
![]() $(z_{ij})_{i,j \in [n]}$
. For
$(z_{ij})_{i,j \in [n]}$
. For
![]() $w \in S_n$
, let
$w \in S_n$
, let
![]() $I_w \subseteq \mathbb {C}[z_{ij} : i,j \in [n]] = \mathbb {C}[\mathsf {Mat}_n]$
be the ideal generated by all
$I_w \subseteq \mathbb {C}[z_{ij} : i,j \in [n]] = \mathbb {C}[\mathsf {Mat}_n]$
be the ideal generated by all
![]() $(\operatorname {\mathrm {rank}} w_{[i][j]}+1) \times (\operatorname {\mathrm {rank}} w_{[i][j]}+1)$
minors of
$(\operatorname {\mathrm {rank}} w_{[i][j]}+1) \times (\operatorname {\mathrm {rank}} w_{[i][j]}+1)$
minors of
![]() $\mathcal {Z}_{[i][j]}$
for
$\mathcal {Z}_{[i][j]}$
for
![]() $i,j \in [n]$
. The vanishing locus of
$i,j \in [n]$
. The vanishing locus of
![]() $I_w$
in the space
$I_w$
in the space
![]() $\mathsf {Mat}_n$
of
$\mathsf {Mat}_n$
of
![]() $n\times n$
complex matrices is exactly the matrix Schubert variety
$n\times n$
complex matrices is exactly the matrix Schubert variety
![]() $MX_w$
.
$MX_w$
.
Let
![]() $\operatorname {\mathrm {\mathsf {init}}}(I_w)$
be the initial ideal of leading terms in
$\operatorname {\mathrm {\mathsf {init}}}(I_w)$
be the initial ideal of leading terms in
![]() $I_w$
with respect to any term order on
$I_w$
with respect to any term order on
![]() $\mathbb {C}[z_{ij}]$
with the property that the leading term of
$\mathbb {C}[z_{ij}]$
with the property that the leading term of
![]() $\det (A)$
for any submatrix A of
$\det (A)$
for any submatrix A of
![]() $\mathcal {Z}$
is the product of the antidiagonal entries of A. For instance, lexicographic order with the variable ordering
$\mathcal {Z}$
is the product of the antidiagonal entries of A. For instance, lexicographic order with the variable ordering
![]() $z_{1n} < \cdots < z_{11} < z_{2n} < \cdots < z_{21} < \cdots $
has this property.
$z_{1n} < \cdots < z_{11} < z_{2n} < \cdots < z_{21} < \cdots $
has this property.
Theorem 6.5 ([Reference Knutson and Miller23])
For each permutation
![]() $w \in S_n$
, the ideal
$w \in S_n$
, the ideal
![]() $I_w$
is prime, and there is a prime decomposition
$I_w$
is prime, and there is a prime decomposition
![]() $ \operatorname {\mathrm {\mathsf {init}}}(I_w) = \bigcap _{D \in \mathcal {PD}(w)} (z_{ij} : (i,j) \in D) $
.
$ \operatorname {\mathrm {\mathsf {init}}}(I_w) = \bigcap _{D \in \mathcal {PD}(w)} (z_{ij} : (i,j) \in D) $
.
Given the description of the class
![]() $[MX_w]$
in Section 2.2, this result implies the pipe dream formula (1.2) for
$[MX_w]$
in Section 2.2, this result implies the pipe dream formula (1.2) for
![]() $[MX_w] = \mathfrak {S}_w(x,y)$
.
$[MX_w] = \mathfrak {S}_w(x,y)$
.
Now let
![]() $\hat {\mathcal {Z}}$
be the symmetric matrix of indeterminates
$\hat {\mathcal {Z}}$
be the symmetric matrix of indeterminates
![]() $[z_{\max (i,j), \min (i,j)}]_{i,j \in [n]}$
. Define
$[z_{\max (i,j), \min (i,j)}]_{i,j \in [n]}$
. Define
![]() $\hat I_y \subseteq \mathbb {C}[z_{ij} : 1 \leq j < i \leq n] = \mathbb {C}[\mathsf {SMat}_n]$
for
$\hat I_y \subseteq \mathbb {C}[z_{ij} : 1 \leq j < i \leq n] = \mathbb {C}[\mathsf {SMat}_n]$
for
![]() $y \in \mathcal {I}_n$
to be the ideal generated by all
$y \in \mathcal {I}_n$
to be the ideal generated by all
![]() $(1+\operatorname {\mathrm {rank}} y_{[i][j]}) \times (1+\operatorname {\mathrm {rank}} y_{[i][j]})$
minors of
$(1+\operatorname {\mathrm {rank}} y_{[i][j]}) \times (1+\operatorname {\mathrm {rank}} y_{[i][j]})$
minors of
![]() $\hat {\mathcal {Z}}_{[i][j]}$
for
$\hat {\mathcal {Z}}_{[i][j]}$
for
![]() $i,j \in [n]$
. The vanishing locus of
$i,j \in [n]$
. The vanishing locus of
![]() $\hat I_y$
is
$\hat I_y$
is
![]() $M\hat X_y$
.
$M\hat X_y$
.
Conjecture 6.6 For
![]() $y \in \mathcal {I}_n$
, the ideal
$y \in \mathcal {I}_n$
, the ideal
![]() $\hat I_y$
is prime, and there is a primary decomposition of
$\hat I_y$
is prime, and there is a primary decomposition of
![]() $\operatorname {\mathrm {\mathsf {init}}}(\hat I_y)$
whose top-dimensional components are
$\operatorname {\mathrm {\mathsf {init}}}(\hat I_y)$
whose top-dimensional components are
![]() $\left (z_{ij}^{m_{ij,D}} : (i,j) \in D\right )$
for
$\left (z_{ij}^{m_{ij,D}} : (i,j) \in D\right )$
for
![]() $D \in \mathcal {ID}(y)$
, where
$D \in \mathcal {ID}(y)$
, where
![]() $m_{ij,D}=2$
if the pipes crossing at
$m_{ij,D}=2$
if the pipes crossing at
![]() $(i,j)$
are labeled p and
$(i,j)$
are labeled p and
![]() $z(p)$
for some
$z(p)$
for some
![]() $p\in [n]$
, and otherwise
$p\in [n]$
, and otherwise
![]() $m_{ij,D}=1$
.
$m_{ij,D}=1$
.
As per Section 2.2, the conjecture would give a direct geometric proof of Theorem 1.5.
Example 6.7 Let
![]() $y = (3,4) \in \mathcal {I}_4$
. Then
$y = (3,4) \in \mathcal {I}_4$
. Then
![]() $A \in M\hat X_y$
if and only if
$A \in M\hat X_y$
if and only if
![]() $\operatorname {\mathrm {rank}} A_{[i][j]} \leq m_{ij}$
for
$\operatorname {\mathrm {rank}} A_{[i][j]} \leq m_{ij}$
for
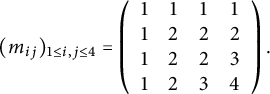 $$ \begin{align*} (m_{ij})_{1\leq i,j\leq 4} = \left(\begin{array}{cccc} 1 & 1 & 1 & 1\\ 1 & 2 & 2 & 2\\ 1 & 2 & 2 & 3\\ 1 & 2 & 3 & 4 \end{array}\right). \end{align*} $$
$$ \begin{align*} (m_{ij})_{1\leq i,j\leq 4} = \left(\begin{array}{cccc} 1 & 1 & 1 & 1\\ 1 & 2 & 2 & 2\\ 1 & 2 & 2 & 3\\ 1 & 2 & 3 & 4 \end{array}\right). \end{align*} $$
These rank conditions all follow from
![]() $\operatorname {\mathrm {rank}} A_{[3][3]} \leq 2$
, so
$\operatorname {\mathrm {rank}} A_{[3][3]} \leq 2$
, so
![]() $\hat I_y$
is generated by
$\hat I_y$
is generated by
![]() $\det \hat {\mathcal {Z}}_{[3][3]}$
. The ideals in the primary decomposition
$\det \hat {\mathcal {Z}}_{[3][3]}$
. The ideals in the primary decomposition
![]() $\operatorname {\mathrm {\mathsf {init}}}(\hat I_y) = (z_{31}^2 z_{22}) = (z_{31}^2) \cap (z_{22})$
correspond to the two involution pipe dreams in the set
$\operatorname {\mathrm {\mathsf {init}}}(\hat I_y) = (z_{31}^2 z_{22}) = (z_{31}^2) \cap (z_{22})$
correspond to the two involution pipe dreams in the set
![]() $ \mathcal {ID}(y) = \{ \{ (3,1)\}, \{(2,2)\}\} $
for
$ \mathcal {ID}(y) = \{ \{ (3,1)\}, \{(2,2)\}\} $
for
![]() $y=(3,4)$
.
$y=(3,4)$
.
Example 6.8 Let
![]() $y = 14523 = (2,4)(3,5) \in \mathcal {I}_5$
. One computes that
$y = 14523 = (2,4)(3,5) \in \mathcal {I}_5$
. One computes that
There is a single involution pipe dream for y given by
![]() $\{(2,1),(3,1),(3,2)\}.$
This pipe dream corresponds to the codimension
$\{(2,1),(3,1),(3,2)\}.$
This pipe dream corresponds to the codimension
![]() $3$
component
$3$
component
![]() $(z_{21}^2, z_{31}, z_{32}^2)$
of
$(z_{21}^2, z_{31}, z_{32}^2)$
of
![]() $\operatorname {\mathrm {\mathsf {init}}}(\hat I_y)$
, while the codimension
$\operatorname {\mathrm {\mathsf {init}}}(\hat I_y)$
, while the codimension
![]() $4$
component
$4$
component
![]() $(z_{21}, z_{22}, z_{31}^2, z_{32})$
does not correspond to a pipe dream of y.
$(z_{21}, z_{22}, z_{31}^2, z_{32})$
does not correspond to a pipe dream of y.
For
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
, the ideal generated by the
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
, the ideal generated by the
![]() $(\operatorname {\mathrm {rank}} z_{[i][j]}+1) \times (\operatorname {\mathrm {rank}} z_{[i][j]}+1)$
of a skew-symmetric matrix of indeterminates need not be prime, and we do not have an analogue of Conjecture 6.6.
$(\operatorname {\mathrm {rank}} z_{[i][j]}+1) \times (\operatorname {\mathrm {rank}} z_{[i][j]}+1)$
of a skew-symmetric matrix of indeterminates need not be prime, and we do not have an analogue of Conjecture 6.6.
6.3 Pipe dream formulas for K-theory
A third source of open problems concerns pipe dreams for K-theory. A subset
![]() $D\subseteq [n]\times [n]$
is a K-theoretic pipe dream for
$D\subseteq [n]\times [n]$
is a K-theoretic pipe dream for
![]() $w \in S_n$
if
$w \in S_n$
if
![]() $\mathsf {word}(D) = (a_1,a_2,\dots ,a_p)$
satisfies
$\mathsf {word}(D) = (a_1,a_2,\dots ,a_p)$
satisfies
![]() $ s_{a_1} \circ s_{a_2} \circ \dots \circ s_{a_p} = w $
where
$ s_{a_1} \circ s_{a_2} \circ \dots \circ s_{a_p} = w $
where
![]() $\circ $
is the Demazure product. Let
$\circ $
is the Demazure product. Let
![]() $\mathcal {KPD}(w)$
denote the set of K-theoretic pipe dreams of w. Fomin and Kirillov [Reference Fomin and Kirillov7] introduce these objects in order to state this formula for the (generalized) Grothendieck polynomial
$\mathcal {KPD}(w)$
denote the set of K-theoretic pipe dreams of w. Fomin and Kirillov [Reference Fomin and Kirillov7] introduce these objects in order to state this formula for the (generalized) Grothendieck polynomial
![]() $\mathfrak {G}_w$
of
$\mathfrak {G}_w$
of
![]() $w\in S_n$
:
$w\in S_n$
:
This identity is nontrivial to derive from Lascoux and Schützenberger’s original definition of Grothendieck polynomials in terms of isobaric divided difference operators [Reference Lascoux26, Reference Lascoux and Schützenberger28].
Grothendieck polynomials becomes Schubert polynomials on setting
![]() $\beta =0$
. In [Reference Marberg31, Reference Marberg and Pawlowski33], continuing work of Wyser and Yong [Reference Wyser and Yong45], the second two authors studied orthogonal and symplectic Grothendieck polynomials
$\beta =0$
. In [Reference Marberg31, Reference Marberg and Pawlowski33], continuing work of Wyser and Yong [Reference Wyser and Yong45], the second two authors studied orthogonal and symplectic Grothendieck polynomials
![]() $\mathfrak {G}^{\mathsf {O}}_y$
and
$\mathfrak {G}^{\mathsf {O}}_y$
and
![]() $\mathfrak {G}^{\mathsf {Sp}}_z$
indexed by
$\mathfrak {G}^{\mathsf {Sp}}_z$
indexed by
![]() $y \in \mathcal {I}_n$
and
$y \in \mathcal {I}_n$
and
![]() $z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
. These polynomials likewise recover the involution Schubert polynomials
$z \in \mathcal {I}^{\mathsf {{FPF}}}_n$
. These polynomials likewise recover the involution Schubert polynomials
![]() $\hat {\mathfrak {S}}_y$
and
$\hat {\mathfrak {S}}_y$
and
![]() $\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
on setting
$\hat {\mathfrak {S}}^{\mathsf {{FPF}}}_z$
on setting
![]() $\beta =0$
, and it would be interesting to know if they have analogous pipe dream formulas.
$\beta =0$
, and it would be interesting to know if they have analogous pipe dream formulas.
The symplectic case of this question is more tractable. The polynomials
![]() $\mathfrak {G}^{\mathsf {Sp}}_z$
have a formulation in terms of isobaric divided difference operators due to Wyser and Yong [Reference Wyser and Yong45], which suggests a natural K-theoretic variant of the set
$\mathfrak {G}^{\mathsf {Sp}}_z$
have a formulation in terms of isobaric divided difference operators due to Wyser and Yong [Reference Wyser and Yong45], which suggests a natural K-theoretic variant of the set
![]() $\mathcal {FD}(z)$
. A formula for
$\mathcal {FD}(z)$
. A formula for
![]() $\mathfrak {G}^{\mathsf {Sp}}_z$
involving these objects appears in [Reference Marberg and Pawlowski33, Section 4]. By contrast, no simple algebraic formula is known for the polynomials
$\mathfrak {G}^{\mathsf {Sp}}_z$
involving these objects appears in [Reference Marberg and Pawlowski33, Section 4]. By contrast, no simple algebraic formula is known for the polynomials
![]() $\mathfrak {G}^{\mathsf {O}}_y$
. It is a nontrivial problem even to identify the correct K-theoretic generalization of
$\mathfrak {G}^{\mathsf {O}}_y$
. It is a nontrivial problem even to identify the correct K-theoretic generalization of
![]() $\mathcal {ID}(y)$
.
$\mathcal {ID}(y)$
.
Problem 6.9 Find a pipe dream formula for the polynomials
![]() $\mathfrak {G}^{\mathsf {O}}_y$
involving an appropriate “K-theoretic” generalization of the sets of involution pipe dreams
$\mathfrak {G}^{\mathsf {O}}_y$
involving an appropriate “K-theoretic” generalization of the sets of involution pipe dreams
![]() $\mathcal {ID}(y)$
.
$\mathcal {ID}(y)$
.
Acknowledgement
This work was partially supported by Hong Kong RGC Grant ECS 26305218. We thank Allen Knutson for explaining to us his proof of (1.2) prior to the appearance of [Reference Knutson22].