Hostname: page-component-cb9f654ff-lqqdg Total loading time: 0 Render date: 2025-09-01T23:03:42.064Z Has data issue: false hasContentIssue false
  • English
  • Français

Maranda’s theorem for pure-injective modules and duality

Part of: Model theory Representation theory of rings and algebras

Published online by Cambridge University Press:  17 March 2022

Lorna Gregory Open the ORCID record for Lorna Gregory [Opens in a new window]
Lorna Gregory*
Affiliation:
Dipartimento di Matematica e Fisica, Università degli Studi della Campania “Luigi Vanvitelli,” Viale Abramo Lincoln, 5, 81100 Caserta CE, Italy
*
e-mail: Lorna.Gregory@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let R be a discrete valuation domain with field of fractions Q and maximal ideal generated by 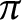$\pi $. Let 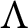$\Lambda $ be an R-order such that 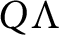$Q\Lambda $ is a separable Q-algebra. Maranda showed that there exists 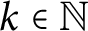$k\in \mathbb {N}$ such that for all 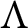$\Lambda $-lattices L and M, if 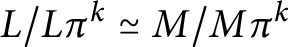$L/L\pi ^k\simeq M/M\pi ^k$, then 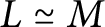$L\simeq M$. Moreover, if R is complete and L is an indecomposable 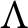$\Lambda $-lattice, then 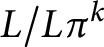$L/L\pi ^k$ is also indecomposable. We extend Maranda’s theorem to the class of R-reduced R-torsion-free pure-injective 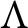$\Lambda $-modules.

As an application of this extension, we show that if 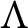$\Lambda $ is an order over a Dedekind domain R with field of fractions Q such that 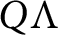$Q\Lambda $ is separable, then the lattice of open subsets of the R-torsion-free part of the right Ziegler spectrum of 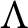$\Lambda $ is isomorphic to the lattice of open subsets of the R-torsion-free part of the left Ziegler spectrum of 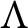$\Lambda $.

Furthermore, with k as in Maranda’s theorem, we show that if M is R-torsion-free and 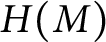$H(M)$ is the pure-injective hull of M, then 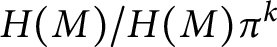$H(M)/H(M)\pi ^k$ is the pure-injective hull of 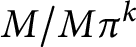$M/M\pi ^k$. We use this result to give a characterization of R-torsion-free pure-injective 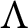$\Lambda $-modules and describe the pure-injective hulls of certain R-torsion-free 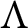$\Lambda $-modules.

Keywords

Order over a Dedekind domainpure-injectiveZiegler spectrum

MSC classification

Primary: 03C60: Model-theoretic algebra
Secondary: 03C98: Applications of model theory 16G30: Representations of orders, lattices, algebras over commutative rings 16H20: Lattices over orders

Information

Type
Article
Information
Canadian Journal of Mathematics , Volume 75 , Issue 2 , April 2023 , pp. 581 - 607
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The majority of this work was completed while the author was employed by the University of Camerino.

References

Bondarenko, V. M., The similarity of matrices over rings of residue classes . In: Mathematics collection (Russian), Naukova Dumka, Kiev, 1976, pp. 275–277.Google Scholar
Butler, M. C. R., The 2-adic representations of Klein’s four group . In: Proceedings of the Second International Conference on the Theory of Groups (Australian Nat. Univ., Canberra, 1973), Lecture Notes in Mathematics, 372, Springer-Verlag, Berlin, Heidelberg, New York, 1974, pp. 197–203.CrossRefGoogle Scholar
Butler, M. C. R., On the classification of local integral representations of finite abelian p-groups . In: Proceedings of the International Conference on Representations of Algebras (Carleton Univ., Ottawa, Ont., 1974), Paper No. 6, Carleton Mathematical Lecture Notes, 9, Springer-Verlag, Berlin, Heidelberg, New York, 1974, 18 pp.Google Scholar
Butler, M. C. R., Campbell, J. M., and Kovács, L. G., On infinite rank integral representations of groups and orders of finite lattice type. Arch. Math. (Basel) 83(2004), no. 4, 297–308.CrossRefGoogle Scholar
Curtis, C. W. and Reiner, I., Methods of representation theory. Vol. I, John Wiley & Sons, Inc., New York, 1981. With applications to finite groups and orders, Pure and Applied Mathematics, A Wiley-Interscience Publication.Google Scholar
Dieterich, E., Construction of Auslander–Reiten quivers for a class of group rings. Math. Z. 184(1983), no. 1, 43–60.CrossRefGoogle Scholar
Geigle, W., The Krull–Gabriel dimension of the representation theory of a tame hereditary Artin algebra and applications to the structure of exact sequences. Manuscripta Math. 54(1985), nos. 1–2, 83–106.CrossRefGoogle Scholar
Gregory, L., L’Innocente, S., and Toffalori, C., The torsion-free part of the Ziegler spectrum of orders over Dedekind domains. MLQ Math. Log. Q. 66(2020), no. 1, 20–36.CrossRefGoogle Scholar
Herzog, I., Elementary duality of modules. Trans. Amer. Math. Soc. 340(1993), no. 1, 37–69.CrossRefGoogle Scholar
Herzog, I., The endomorphism ring of a localized coherent functor. J. Algebra 191(1997), no. 1, 416–426.CrossRefGoogle Scholar
Krause, H., Exactly definable categories. J. Algebra 201(1998), no. 2, 456–492.CrossRefGoogle Scholar
Krause, H., Generic modules over Artin algebras. Proc. Lond. Math. Soc. (3) 76(1998), no. 2, 276–306.CrossRefGoogle Scholar
Maranda, J.-M., On  $B$ -adic integral representations of finite groups. Canad. J. Math. 5(1953), 344–355.CrossRefGoogle Scholar
Marcja, A., Prest, M., and Toffalori, C., The torsionfree part of the Ziegler spectrum of $RG$ when $R$ is a Dedekind domain and $G$ is a finite group. J. Symbolic Logic 67(2002), no. 3, 1126–1140.Google Scholar
Prest, M., Model theory and modules, London Mathematical Society Lecture Note Series, 130, Cambridge University Press, Cambridge, 1988.CrossRefGoogle Scholar
Prest, M., Interpreting modules in modules. Ann. Pure Appl. Logic 88(1997), nos. 2–3, 193–215. Joint AILA-KGS Model Theory Meeting (Florence, 1995).CrossRefGoogle Scholar
Prest, M., Purity, spectra and localisation, Encyclopedia of Mathematics and Its Applications, 121, Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
Prest, M., Definable additive categories: purity and model theory, Memoirs of the American Mathematical Society, 210(987), American Mathematical Society, Providence, RI, 2011, vi + 109.Google Scholar
Příhoda, P. and Puninski, G., Classifying generalized lattices: some examples as an introduction. J. Lond. Math. Soc. (2) 82(2010), no. 1, 125–143.Google Scholar
Puninski, G. and Toffalori, C., The torsion-free part of the Ziegler spectrum of the Klein four group. J. Pure Appl. Algebra 215(2011), no. 8, 1791–1804.CrossRefGoogle Scholar
Roggenkamp, K. W., Lattices over orders. II , Lecture Notes in Mathematics, 142, Springer-Verlag, Berlin–New York, 1970.CrossRefGoogle Scholar
Roggenkamp, K. W. and Schmidt, J. W., Almost split sequences for integral group rings and orders. Comm. Algebra 4(1976), no. 10, 893–917.CrossRefGoogle Scholar
Rump, W., Large lattices over orders. Proc. Lond. Math. Soc. (3) 91(2005), no. 1, 105–128.CrossRefGoogle Scholar
Ziegler, M., Model theory of modules. Ann. Pure Appl. Logic 26(1984), no. 2, 149–213.CrossRefGoogle Scholar