Hostname: page-component-7dd5485656-zklqj Total loading time: 0 Render date: 2025-10-31T12:10:39.464Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal Dynamical Systems on Connected Odd Dimensional Spaces

Published online by Cambridge University Press:  20 November 2018

Huaxin Lin
Huaxin Lin*
Affiliation:
Department of Mathematics, East China Normal University, Shanghai, China 20062 and , Department of Mathematics, University of Oregon, Eugene, Oregon 97402, USA e-mail: hlin@uoregon.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 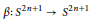$\beta:\,{{S}^{2n+1}}\,\to \,{{S}^{2n+1}}$ be a minimal homeomorphism 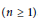$\left( n\,\ge \,1 \right)$ . We show that the crossed product 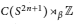$C\left( {{S}^{2n+1}} \right)\,{{\rtimes }_{\beta}}\mathbb{Z}$ has rational tracial rank at most one. Let 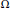$\Omega $ be a connected, compact, metric space with finite covering dimension and with 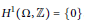${{H}^{1}}\left( \Omega ,\,\mathbb{Z} \right)\,=\,\left\{ 0 \right\}$ . Suppose that 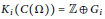${{K}_{i}}\left( C\left( \Omega\right) \right)\,=\,\mathbb{Z}\,\oplus \,{{G}_{i}}$ , where 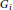${{G}_{i}}$ is a finite abelian group, 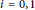$i\,=\,0,\,1$ . Let 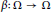$\beta :\,\Omega \,\to \,\Omega $ be a minimal homeomorphism. We also show that 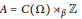$A\,=\,C\left( \Omega\right)\,{{\rtimes }_{\beta}}\,\mathbb{Z}$ has rational tracial rank at most one and is classifiable. In particular, this applies to the minimal dynamical systems on odd dimensional real projective spaces. This is done by studying minimal homeomorphisms on 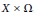$X\,\times \,\Omega $ , where 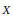$X$ is the Cantor set.

Keywords

46L3546L05Minimal dynamical systems

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 4 , 01 August 2015 , pp. 870 - 892
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Blackadar, B., K-theoryfor operator algebras. Mathematical Sciences Research Institute Publications, 5. Springer-Verlag, New York, 1986.Google Scholar
[2] Dadarlat, M. and Loring, T. A., A universal multicoefficient theorem for the Kasparov groups. Duke Math. J. 84(1996), no. 2, 355–377.http://dx.doi.org/10.1215/S0012-7094-96-08412-4 Google Scholar
[3] de Vries, J., Elements of topological dynamics. Mathematics and its Applications, 257, Kluwer Academic Publishers Group, Dordrecht, 1993.Google Scholar
[4] Elliott, G. A. and Evans, E. D., The structure of the irrational rotation C*-algebras. Ann. of Math. 138(1993), no. 3, 477–501.http://dx.doi.org/10.2307/2946553 Google Scholar
[5] Exel, R., Rotation numbers for automorphisms of C*-algebras. Pacific J. Math. 127(1987), 31–89.http://dx.doi.org/10.2140/pjm.1987.127.31 Google Scholar
[6] Fathi, A. and Herman, M. R., Existence de diffeomorphismes minimaux. Dynamical systems, Vol. I—Warsaw, Astérisque, 49, Soc. Math. France, Paris, 1977, pp. 37–59.Google Scholar
[7] Giordano, T., Putnam, I. F., and Skau, C. F., Topological orbit equivalence and C*-crossedproducts. J. Reine Angew. Math. 469(1995), 51–111.Google Scholar
[8] Herman, R., Putnam, I. F., and Skau, C. F., Ordered Bratteli diagrams, dimension groups and topological dynamics. Internat. J. Math. 3(1992), no. 6, 827–864.http://dx.doi.org/10.1142/S0129167X92000382 Google Scholar
[9] Hu, S., Lin, H., and Xue, Y., The tracial topological rank of extensions of C*-algebras. Math. Scand. 94(2004), no. 1, 125–147.Google Scholar
[10] Lin, H., Asymptotic unitary equivalence and classification of simple amenable C*-algebras. Invent. Math. 183(2011), no. 2, 385–450.http://dx.doi.org/10.1007/s00222-010-0280-9 Google Scholar
[11] Lin, H., Localizing the Elliott conjecture at strongly self-absorbing *-algebras. II. J. Reine Angew. Math. 692(2014), 233–243.Google Scholar
[12] Lin, H., Homomorphismsfrom AH-algebras. arxiv:1102.4631Google Scholar
[13] Lin, H., On local AH algebras. Memoir. Amer. Math. Soc. 235(2015), to appear. arxiv:1104.0445.Google Scholar
[14] Lin, H. and Matui, H., Minimal dynamical systems on the product of the Cantor set and the circle. Comm. Math. Phys. 257(2005), no. 2, 425–471.http://dx.doi.org/10.1007/s00220-005-1298-5 Google Scholar
[15] Lin, H. and Matui, H., Minimal dynamical systems on the product of the Cantor set and the circle. II. Selecta Math. (N.S.) 12(2006), 199–239.http://dx.doi.org/10.1007/s00029-006-0025-1 Google Scholar
[16] Lin, H. and Niu, Z., Lifting KK-elements, asymptotic unitary equivalence and classification of simple C*-algebras. Adv. Math. 219(2008), no. 5, 1729–1769.http://dx.doi.Org/10.1016/j.aim.2008.07.011 Google Scholar
[17] Lin, H. and Niu, Z., The range of a class of classifiable separable simple amenable C*-algebras. J. Funct. Anal. 260(2011), no. 1, 1–29.http://dx.doi.Org/10.1016/j.jfa.2010.08.019 Google Scholar
[18] Lin, H. and Sun, W., Tensor products of classifiable C*-algebras. arxiv:1203.3737Google Scholar
[19] Lin, H. and Phillips, N. C., Crossed products by minimal homeomorphisms. J. Reine Angew. Math. 641(2010), 95–122.Google Scholar
[20] Matui, H., Approximate conjugacy and full groups of Cantor minimal systems. Publ. Res. Inst. Math. Sci. 41(2005), no. 3, 695–722. http://dx.doi.Org/10.2977/prims/1145475227 Google Scholar
[21] Pimsner, M. and Voiculescu, D., Exact sequences for K–groups and Ext–groups of certain cross-product C*-algebras. J. Operator Theory 4(1980), no. 1, 93–118.Google Scholar
[22] Putnam, I. F., The C*-algebras associated with minimal homeomorphisms of the Cantor set. Pacific J. Math. 136(1989), no. 2, 329–353.http://dx.doi.Org/10.2140/pjm.1989.136.329 Google Scholar
[23] Rørdam, M., On the structure of simple C*-algebras tensored with a UHF-algebra. II. J. Funct. Anal. 107(1992), no. 2, 255–269.http://dx.doi.Org/10.1016/0022-1236(92)90106-S Google Scholar
[24] Strung, K., C*-algebras of minimal dynamical systems of the product of a Cantor set and an odd dimensional sphere. arxiv:1403.3136Google Scholar
[25] Sun, W., Crossed product C*-algebras of minimal dynamical systems on the product of the Cantor set and the torus. J. Funct. Anal. 265(2013), no. 7, 1105–1169.http://dx.doi.Org/10.1016/j.jfa.2013.05.025 Google Scholar
[26] Thomsen, K., Traces, unitary characters and crossed products by Z. Publ. Res. Inst. Math. Sci. 31(1995), no. 6, 1011–1029.http://dx.doi.org/10.2977/prims/1195163594 Google Scholar
[27] Toms, A. S. and Winter, W., Minimal dynamics and the classification of C*-algebras. Proc. Natl. Acad. Sci. USA 106(2009), no. 40, 16942–16943.http://dx.doi.org/10.1073/pnas.0903629106 Google Scholar
[28] Windsor, A., Minimal but not uniquely ergodic diffeomorphisms. In: Smooth ergodic theory and its applications (Seattle, WA, 1999), Proc. Sympos. Pure Math., 69, American Mathematical Society, Providence, RI, 2001, pp. 809–824.Google Scholar
[29] Winter, W., Localizing the Elliott conjecture at strongly self-absorbing C*-algebras. J. Reine Angew. Math. 692(2014), 193–231.Google Scholar
[30] Winter, W., Classifying crossed product C*-algebras. arxiv:1308.5084Google Scholar