Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-29T05:52:48.836Z Has data issue: false hasContentIssue false
  • English
  • Français

On Geometric Flats in the CAT(0) Realization of Coxeter Groups and Tits Buildings

Published online by Cambridge University Press:  20 November 2018

Pierre-Emmanuel Caprace  and
Frédéric Haglund
Pierre-Emmanuel Caprace
Affiliation:
Département de Mathématiques, Université libre de Bruxelles, CP216, Bd du Triomphe, 1050 Bruxelles, Belgium, e-mail: pcaprace@ulb.ac.be
Frédéric Haglund
Affiliation:
Département de Mathématiques, Université libre de Bruxelles, CP216, Bd du Triomphe, 1050 Bruxelles, Belgium, e-mail: pcaprace@ulb.ac.be
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

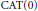Given a complete $\text{CAT}(0)$ space 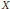$X$ endowed with a geometric action of a group 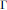$\Gamma $, it is known that if 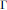$\Gamma $ contains a free abelian group of rank $n$, then 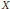$X$ contains a geometric flat of dimension $n$. We prove the converse of this statement in the special case where 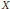$X$ is a convex subcomplex of the 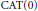$\text{CAT}(0)$ realization of a Coxeter group $W$, and 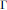$\Gamma $ is a subgroup of $W$. In particular a convex cocompact subgroup of a Coxeter group is Gromov-hyperbolic if and only if it does not contain a free abelian group of rank 2. Our result also provides an explicit control on geometric flats in the 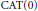$\text{CAT}(0)$ realization of arbitrary Tits buildings.

Keywords

20F5551F1553C2320E4251E24Coxeter groupflat rankCAT(0) spacebuilding
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 4 , 01 August 2009 , pp. 740 - 761
Copyright
Copyright © Canadian Mathematical Society 2012

References

[BH93] Brink, B. and Howlett, R. B., A finiteness property and an automatic structure for Coxeter groups. Math. Ann. 296(1993), no. 1, 179–190.Google Scholar
[BH99] Bridson, M. R. and Haefliger, A., Metric spaces of non-positive curvature. Grundlehren der MathematischenWissenschaften 319, Springer-Verlag, Berlin, 1999.Google Scholar
[BRW05] Baumgartner, U., Rémy, B., and Willis, G. A., Flat rank of automorphism groups of buildings. Transform. Groups 12(2007), no. 3, 413–436.Google Scholar
[Cap06] Caprace, P.-E., Conjugacy of 2-spherical subgroups of Coxeter groups and parallel walls. Algebr. Geom. Topol. 6(2006), 1987–2029.Google Scholar
[C M05] Caprace, P.-E. and Mühlherr, B., Reflection triangles in Coxeter groups and biautomaticity. J. Group Theory, 8(2005), no. 4, 467–489.Google Scholar
[Dav98] Davis, M., Buildings are CAT(0). In: Geometry and Cohomology in Group Theory. London Math. Soc. Lecture Note Ser. 252, Cambridge, 1998. Cambridge University Press, 1988, pp. 108–123..Google Scholar
[Deo89] Deodhar, V. V., A note on subgroups generated by reflections in Coxeter groups. Arch. Math. (Basel), 53(1989), no. 6, 543–546.Google Scholar
[Gro93] Gromov, M., Asymptotic invariants of infinite groups. In: Geometric Group Theory. London Math. Soc. Lecture Note Ser. 182, Cambridge, Cambridge University Press, 1993, pp. 1–295.Google Scholar
[HP98] Haglund, F. and Paulin, F., Simplicité de groupes d’automorphismes d’espaces à courbure négative. In: The Epstein birthday schrift. Geom. Topol. Monogr. 1. Geom. Topol. Publ., 1988, pp. 181–248.Google Scholar
[HW06] Haglund, F. and Wise, D., Special cube complexes. Geom. Funct. Anal. 17(2008, no. 5, 1551–1620.Google Scholar
[Hum90] Humphreys, J. E., Reflection Groups and Coxeter Groups. Cambridge Studies in Advanced Mathematics 29. Cambridge University Press, Cambridge, 1990.Google Scholar
[KK04] Kapovich, M. and Kleiner, B., The weak hyperbolization conjecture for 3-dimensional CAT(0) groups. Groups Geom. Dyn. 1(2007), no. 1, 61–79.Google Scholar
[Kle99] Kleiner, B., The local structure of length spaces with curvature bounded above. Math. Z. 231(1999), no. 3, 409–456.Google Scholar
[Kra94] Krammer, D., The Conjugacy Problem for Coxeter Groups. Ph.D. thesis, Universiteit Utrecht, 1994. http://www.maths.warwick.ac.uk/\%7Edaan/index files/Proefschrift12.dvi. Google Scholar
[NR03] Niblo, G. A. and Reeves, L. D., Coxeter groups act on CAT(0) cube complexes. J. Group Theory 6(2003), no. 3, 399–413.Google Scholar
[NV02] Noskov, G. and Vinberg, E., Strong Tits alternative for subgroups of Coxeter groups. J. Lie Theory 12(2002), no. 1, 259–264.Google Scholar
[Rém04] Rémy, B., Topological simplicity, commensurator super-rigidity and non linearity of Kac- Moody groups. With an appendix by P. Bonvin. Geom. Funct. Anal. 14(2004), no. 4, 810–852.Google Scholar
[Ron89] Ronan, M., Lectures on Buildings. Perspectives in Mathematics 7. Academic Press, Boston, 1989.Google Scholar
[Tit81] Tits, J., A local approach to buildings. In: The Geometric Vein. Springer, New York, 1981, pp. 519–547.Google Scholar
[Wis05] Wise, D. T., Approximating flats by periodic flats in CAT(0) square complexes. Canad. J. Math. 57(2005), no. 2, 416–448.Google Scholar