Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Moser, L.
1963.
On the Sum of Consecutive Primes.
Canadian Mathematical Bulletin,
Vol. 6,
Issue. 2,
p.
159.
Andrushkiw, Joseph W.
Andrushkiw, Roman I.
and
Corzatt, Clifton E.
1976.
Representations of Positive Integers as Sums of Arithmetic Progressions.
Mathematics Magazine,
Vol. 49,
Issue. 5,
p.
245.
Guy, Robert
1982.
Sums of Consecutive Integers.
The Fibonacci Quarterly,
Vol. 20,
Issue. 1,
p.
36.
Gamer, Carlton
Roeder, David W.
and
Watkins, John J.
1985.
Trapezoidal Numbers.
Mathematics Magazine,
Vol. 58,
Issue. 2,
p.
108.
Robertson, Jack M.
and
Webb, William A.
1991.
Sieving with sums.
The Mathematical Gazette,
Vol. 75,
Issue. 472,
p.
171.
Pong, Wai Yan
2007.
Sums of Consecutive Integers.
The College Mathematics Journal,
Vol. 38,
Issue. 2,
p.
119.
PONG, WAI YAN
2009.
LENGTH SPECTRA OF NATURAL NUMBERS.
International Journal of Number Theory,
Vol. 05,
Issue. 06,
p.
1089.
TSAI, MU-TSUN
and
ZAHARESCU, ALEXANDRU
2012.
ON THE SUM OF CONSECUTIVE INTEGERS IN SEQUENCES II.
International Journal of Number Theory,
Vol. 08,
Issue. 05,
p.
1281.
TSAI, MU-TSUN
and
ZAHARESCU, ALEXANDRU
2012.
ON THE SUM OF CONSECUTIVE INTEGERS IN SEQUENCES.
International Journal of Number Theory,
Vol. 08,
Issue. 03,
p.
643.
Bonomo, John P.
2014.
Not All Numbers Can Be Created Equally.
The College Mathematics Journal,
Vol. 45,
Issue. 1,
p.
3.
Nathanson, Melvyn B.
2017.
Analytic Number Theory, Modular Forms and q-Hypergeometric Series.
Vol. 221,
Issue. ,
p.
555.

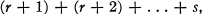
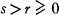 . It is shown that
. It is shown that 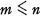 for which
for which