Published online by Cambridge University Press: 09 January 2019
We prove results concerning the multiplicity as well as the Cohen–Macaulay and Gorenstein properties of the special fiber ring 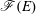 $\mathscr{F}(E)$ of a finitely generated
$\mathscr{F}(E)$ of a finitely generated 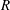 $R$-module
$R$-module 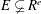 $E\subsetneq R^{e}$ over a Noetherian local ring
$E\subsetneq R^{e}$ over a Noetherian local ring 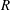 $R$ with infinite residue field. Assuming that
$R$ with infinite residue field. Assuming that 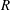 $R$ is Cohen–Macaulay of dimension 1 and that
$R$ is Cohen–Macaulay of dimension 1 and that 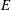 $E$ has finite colength in
$E$ has finite colength in 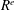 $R^{e}$, our main result establishes an asymptotic length formula for the multiplicity of
$R^{e}$, our main result establishes an asymptotic length formula for the multiplicity of 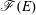 $\mathscr{F}(E)$, which, in addition to being of independent interest, allows us to derive a Cohen–Macaulayness criterion and to detect a curious relation to the Buchsbaum–Rim multiplicity of
$\mathscr{F}(E)$, which, in addition to being of independent interest, allows us to derive a Cohen–Macaulayness criterion and to detect a curious relation to the Buchsbaum–Rim multiplicity of 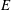 $E$ in this setting. Further, we provide a Gorensteinness characterization for
$E$ in this setting. Further, we provide a Gorensteinness characterization for 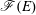 $\mathscr{F}(E)$ in the more general situation where
$\mathscr{F}(E)$ in the more general situation where 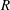 $R$ is Cohen–Macaulay of arbitrary dimension and
$R$ is Cohen–Macaulay of arbitrary dimension and 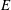 $E$ is not necessarily of finite colength, and we notice a constraint in terms of the second analytic deviation of the module
$E$ is not necessarily of finite colength, and we notice a constraint in terms of the second analytic deviation of the module 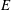 $E$ if its reduction number is at least three.
$E$ if its reduction number is at least three.
The author was partially supported by CAPES-Brazil (grant 88881.121012/2016-01), and by CNPq-Brazil (grant 421440/2016-3).