Hostname: page-component-5447f9dfdb-cjbmw Total loading time: 0 Render date: 2025-07-29T20:58:55.720Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Combinatorics of Gentle Algebras

Part of: Representation theory of rings and algebras

Published online by Cambridge University Press:  29 July 2019

Thomas Brüstle ,
Guillaume Douville ,
Kaveh Mousavand ,
Hugh Thomas  and
Emine Yıldırım
Thomas Brüstle
Affiliation:
Département de Mathématiques, Université de Sherbrooke, 2500, boul. de l’Université Sherbrooke,QC J1K 2R1, Canada, Email: thomas.brustle@usherbrooke.ca
Guillaume Douville
Affiliation:
Département de mathématiques, Université du Québec à Montréal, Montréal, QC H3C 3P8, Canada, Email: douvilleg@gmail.comk.mousavand@lacim.cahugh.ross.thomas@gmail.comemineyyildirim@gmail.com
Kaveh Mousavand
Affiliation:
Département de mathématiques, Université du Québec à Montréal, Montréal, QC H3C 3P8, Canada, Email: douvilleg@gmail.comk.mousavand@lacim.cahugh.ross.thomas@gmail.comemineyyildirim@gmail.com
Hugh Thomas
Affiliation:
Département de mathématiques, Université du Québec à Montréal, Montréal, QC H3C 3P8, Canada, Email: douvilleg@gmail.comk.mousavand@lacim.cahugh.ross.thomas@gmail.comemineyyildirim@gmail.com
Emine Yıldırım
Affiliation:
Département de mathématiques, Université du Québec à Montréal, Montréal, QC H3C 3P8, Canada, Email: douvilleg@gmail.comk.mousavand@lacim.cahugh.ross.thomas@gmail.comemineyyildirim@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

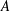For $A$ a gentle algebra, and 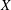$X$ and 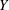$Y$ string modules, we construct a combinatorial basis for 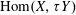$\operatorname{Hom}(X,\unicode[STIX]{x1D70F}Y)$. We use this to describe support $\unicode[STIX]{x1D70F}$-tilting modules for 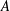$A$. We give a combinatorial realization of maps in both directions realizing the bijection between support $\unicode[STIX]{x1D70F}$-tilting modules and functorially finite torsion classes. We give an explicit basis of 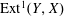$\operatorname{Ext}^{1}(Y,X)$ as short exact sequences. We analyze several constructions given in a more restricted, combinatorial setting by McConville, showing that many but not all of them can be extended to general gentle algebras.

Keywords

gentle algebras𝜏-tilting theory

MSC classification

Primary: 16G20: Representations of quivers and partially ordered sets

Information

Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 6 , December 2020 , pp. 1551 - 1580
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

T. B. was partially supported by an NSERC Discovery Grant. G. D. was partially supported by an NSERC Alexander Graham Bell scholarship. K. M. and E. Y. were partially supported by ISM scholarships. H. T. was partially supported by NSERC and the Canada Research Chairs program.

References

Adachi, T., Iyama, O., and Reiten, I., 𝜏-tilting theory. Compos. Math. 150(2014), 3, 415–452. https://doi.org/10.1112/S0010437X13007422CrossRefGoogle Scholar
Asashiba, H., Derived equivalence classification of algebras. Sugaku Expositions 29(2016), 2, 145–175.Google Scholar
Assem, I., Simson, D., and Skowroński, A., Elements of the representation theory of associative algebras. Cambridge University Press, Cambridge, 2006.CrossRefGoogle Scholar
Auslander, M. and Smalø, S., Almost split sequences in subcategories. J. Algebra 69(1981), 426–454; Addendum: J. Algebra 71 (1981), 592–594. https://doi.org/10.1016/0021-8693(81)90199-XCrossRefGoogle Scholar
Butler, M. C. R. and Ringel, C. M., Auslander–Reiten sequences with few middle terms. Comm. Algebra. 15(1987), 145–179. https://doi.org/10.1080/00927878708823416CrossRefGoogle Scholar
Çanakc˛ı, İ., Pauksztello, D., and Schroll, S., On extensions for gentle algebras. arxiv:1707.06934Google Scholar
Çanakc˛ı, İ. and Schroll, S., Extensions in Jacobian algebras and cluster categories of marked surfaces. Adv. Math. 313(2017), 1–49. https://doi.org/10.1016/j.aim.2017.03.016CrossRefGoogle Scholar
Crawley-Boevey, W., Maps between representations of zero-relation algebras. J. Algebra 126(1989), 259–263. https://doi.org/10.1016/0021-8693(89)90304-9CrossRefGoogle Scholar
Eisele, F., Janssens, G., and Raedschelders, T., A reduction theorem for 𝜏-rigid modules. Math. Z. 290(2018), 3–4, 1377–1413. https://doi.org/10.1007/s00209-018-2067-4CrossRefGoogle Scholar
Garver, A., McConville, T., and Mousavand, K., A categorification of biclosed sets of strings. J. Algebra 546(2020), 390–431. https://doi.org/10.1016/j.jalgebra.2019.10.041CrossRefGoogle Scholar
Geiss, C., Leclerc, B., and Schröer, J., Quivers with relations for symmetrizable Cartan matrices I: Foundations. Invent. Math. 209(2017), 1, 61–158. https://doi.org/10.1007/s00222-016-0705-1CrossRefGoogle Scholar
McConville, T., Lattice structure of grid-Tamari orders. J. Combin. Theory Ser. A 148(2017), 27–56. https://doi.org/10.1016/j.jcta.2016.12.001CrossRefGoogle Scholar
Schröer, J., Modules without self-extensions over gentle algebras. J. Algebra 216(1999), 1, 178–189. https://doi.org/10.1006/jabr.1998.7696CrossRefGoogle Scholar
Palu, Y., Pilaud, V., and Plamondon, P.-G., Non-kissing complexes and 𝜏-tilting for gentle algebras. arxiv:1707.07574.Google Scholar
Weibel, C. A., An introduction to homological algebra. Cambridge Studies in Advanced Mathematics, 38, Cambridge University Press, Cambridge, 1994. https://doi.org/10.1017/CBO9781139644136CrossRefGoogle Scholar