The aim of this paper is to study circular units in the compositum K of t cyclic extensions of 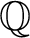${\mathbb {Q}}$ (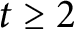$t\ge 2$) of the same odd prime degree 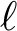$\ell $. If these fields are pairwise arithmetically orthogonal and the number s of primes ramifying in 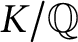$K/{\mathbb {Q}}$ is larger than 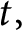$t,$ then a nontrivial root 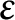$\varepsilon $ of the top generator 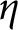$\eta $ of the group of circular units of K is constructed. This explicit unit 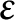$\varepsilon $ is used to define an enlarged group of circular units of K, to show that 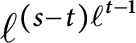$\ell ^{(s-t)\ell ^{t-1}}$ divides the class number of K, and to prove an annihilation statement for the ideal class group of K.