No CrossRef data available.
Article contents
On the Convergence of a Class of Nearly Alternating Series
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $C$ be the class of convex sequences of real numbers. The quadratic irrational numbers can be partitioned into two types as follows. If
$C$ be the class of convex sequences of real numbers. The quadratic irrational numbers can be partitioned into two types as follows. If  $\alpha$ is of the first type and
$\alpha$ is of the first type and 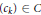 $\left( {{c}_{k}} \right)\,\in C$ , then
$\left( {{c}_{k}} \right)\,\in C$ , then 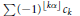 $\sum{{{(-1)}^{\left\lfloor k\alpha\right\rfloor }}}{{c}_{k}}$ converges if and only if
$\sum{{{(-1)}^{\left\lfloor k\alpha\right\rfloor }}}{{c}_{k}}$ converges if and only if 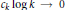 ${{c}_{k}}\log k\to 0$ .If
${{c}_{k}}\log k\to 0$ .If  $\alpha$ is of the second type and
$\alpha$ is of the second type and 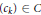 $\left( {{c}_{k}} \right)\,\in C$ , then
$\left( {{c}_{k}} \right)\,\in C$ , then 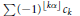 $\sum{{{(-1)}^{\left\lfloor k\alpha\right\rfloor }}}{{c}_{k}}$ converges if and only if
$\sum{{{(-1)}^{\left\lfloor k\alpha\right\rfloor }}}{{c}_{k}}$ converges if and only if 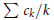 $\sum{{{c}_{k}}/k}$ converges. An example of a quadratic irrational of the first type is
$\sum{{{c}_{k}}/k}$ converges. An example of a quadratic irrational of the first type is 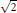 $\sqrt{2}$ , and an example of the second type is
$\sqrt{2}$ , and an example of the second type is 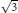 $\sqrt{3}$ . The analysis of this problem relies heavily on the representation of
$\sqrt{3}$ . The analysis of this problem relies heavily on the representation of  $\alpha$ as a simple continued fraction and on properties of the sequences of partial sums
$\alpha$ as a simple continued fraction and on properties of the sequences of partial sums 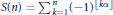 $S\left( n \right)\,=\,{{\sum\nolimits_{k=1}^{n}{\left( -1 \right)}}^{\left\lfloor k\alpha\right\rfloor }}$ and double partial sums
$S\left( n \right)\,=\,{{\sum\nolimits_{k=1}^{n}{\left( -1 \right)}}^{\left\lfloor k\alpha\right\rfloor }}$ and double partial sums 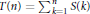 $T\left( n \right)\,=\,\sum\nolimits_{k=1}^{n}{\,S\left( k \right)}$ .
$T\left( n \right)\,=\,\sum\nolimits_{k=1}^{n}{\,S\left( k \right)}$ .
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2007

