Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-28T10:01:35.713Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Neumann Problem for the Schrödinger Equations with Singular Potentials in Lipschitz Domains

Published online by Cambridge University Press:  20 November 2018

Xiangxing Tao  and
Henggeng Wang
Xiangxing Tao
Affiliation:
Department of Mathematics, Ningbo University, Ningbo 315211, The People's Republic of China e-mail: taoxiangxing@nbu.edu.cn
Henggeng Wang
Affiliation:
Department of Mathematics, South-China Normal University, Guangzhou 510631, The People's Republic of China e-mail: wanghg2002@x263.net
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

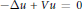We consider the Neumann problem for the Schrödinger equations $-\Delta u\,+\,Vu\,=\,0$, with singular nonnegative potentials 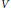$V$ belonging to the reverse Hölder class 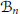${{\mathcal{B}}_{n}}$ , in a connected Lipschitz domain 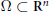$\Omega \,\subset \,{{\text{R}}^{n}}$ . Given boundary data $g$ in 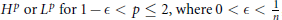${{H}^{p}}\text{or}\,{{L}^{p}}\,\text{for}\,\text{1}-\in \,<\,p\,\le \,2,\text{where}\,\text{0}<\in <\frac{1}{n}$ , it is shown that there is a unique solution, $u$, that solves the Neumann problem for the given data and such that the nontangential maximal function of 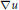$\nabla u$ is in 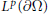${{L}^{p}}(\partial \Omega )$. Moreover, the uniform estimates are found.

Keywords

42B2035J10Neumann problemSchrödinger equationLipschitz domainreverse Hölder classHp space
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 3 , 01 June 2004 , pp. 655 - 672
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Brown, R. M., The Neumann problem on Lipschitz domains in Hardy spaces of order less than one. Pacific J. Math. 171(2)(1995), 389–407.Google Scholar
[2] Coifmain, R., McIntosh, A. and Meyer, Y., L'integral de Cauchy definit un operateur borne sur L2 pour les courbes Lipschitziennes. Ann. of Math. 116(1982), 361–388.Google Scholar
[3] Dahlberg, B. and Kening, C., Hard space and the Neumann problem in Lp for Laplace's equation in Lipschitz domains. Ann. of Math. 125(1987), 437–464.Google Scholar
[4] Fabes, E., Garofalo, N. and Lin, F-H, A partial answer to a conjecture of B. Simon concerning unique continuation. J. Funct. Anal. 88(1990), 1–4–210.Google Scholar
[5] Fabes, E., Jodeit, M. JR and Riviere, N., Potential techniques for boundary value problem on C1-domains. Acta Math. 141(1978), 1–5–184.Google Scholar
[6] Grüter, M. and Kjell-oveWidman, , The Green function for uniformly Elliptic equations. Manuscripta Math. 37(1982), 3–3–342.Google Scholar
[7] Kenig, C. E., Harmonic Analysis Techniques for Second Order Elliptic Boundary Value Problems. Conference Board of the Mathematical Sciences 83(1994), 1–42.Google Scholar
[8] Kenig, C. E. and Pipher, J., The Neumann problem for elliptic equations with non-smooth coefficients. Invent. Math. 113(1993), 447–509.Google Scholar
[9] Muckenhoupt, B., Weighted norm inequality for the Hardy maximal function. Trans. Amer. Math. Soc. 165(1972), 207–227.Google Scholar
[10] Shen, Z., On the Neumann problem for Schrödinger operators in Lipschitz domains. Indiana Univ. Math. J. (1) 43(1994), 143–174.Google Scholar
[11] Shen, Z., Lp estimates for Schrödinger operators with certain potentials. Ann. Inst. Fourier (Grennoble) 45(1995), 513–546.Google Scholar
[12] Stein, E. M., Singular Integral Operators and Differentiability Properties of Functions. Princeton University Press, 1970.Google Scholar