Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-06-08T23:49:41.638Z Has data issue: false hasContentIssue false
  • English
  • Français

Powers in Orbits of Rational Functions: Cases of an Arithmetic Dynamical Mordell–Lang Conjecture

Part of: Arithmetic and non-Archimedean dynamical systems Arithmetic algebraic geometry

Published online by Cambridge University Press:  09 January 2019

Jordan Cahn ,
Rafe Jones  and
Jacob Spear
Jordan Cahn
Affiliation:
Department of Mathematics and Statistics, Carleton College, One North College Street, Northfield, MN 55057, USA Email: jordan.f.cahn@gmail.comrfjones@carleton.eduspearjm77@gmail.com
Rafe Jones
Affiliation:
Department of Mathematics and Statistics, Carleton College, One North College Street, Northfield, MN 55057, USA Email: jordan.f.cahn@gmail.comrfjones@carleton.eduspearjm77@gmail.com
Jacob Spear
Affiliation:
Department of Mathematics and Statistics, Carleton College, One North College Street, Northfield, MN 55057, USA Email: jordan.f.cahn@gmail.comrfjones@carleton.eduspearjm77@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 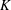$K$ be a finitely generated field of characteristic zero. For fixed 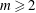$m\geqslant 2$, we study the rational functions 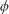$\unicode[STIX]{x1D719}$ defined over 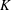$K$ that have a 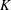$K$-orbit containing infinitely many distinct 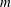$m$-th powers. For 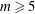$m\geqslant 5$ we show that the only such functions are those of the form 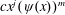$cx^{j}(\unicode[STIX]{x1D713}(x))^{m}$ with 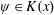$\unicode[STIX]{x1D713}\in K(x)$, and for 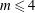$m\leqslant 4$ we show that the only additional cases are certain Lattès maps and four families of rational functions whose special properties appear not to have been studied before.

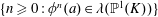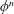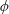With additional analysis, we show that the index set $\{n\geqslant 0:\unicode[STIX]{x1D719}^{n}(a)\in \unicode[STIX]{x1D706}(\mathbb{P}^{1}(K))\}$ is a union of finitely many arithmetic progressions, where $\unicode[STIX]{x1D719}^{n}$ denotes the $n$-th iterate of $\unicode[STIX]{x1D719}$ and 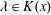$\unicode[STIX]{x1D706}\in K(x)$ is any map Möbius-conjugate over 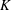$K$ to 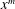$x^{m}$. When the index set is infinite, we give bounds on the number and moduli of the arithmetic progressions involved. These results are similar in flavor to the dynamical Mordell–Lang conjecture, and motivate a new conjecture on the intersection of an orbit with the value set of a morphism. A key ingredient in our proofs is a study of the curves 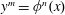$y^{m}=\unicode[STIX]{x1D719}^{n}(x)$. We describe all 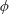$\unicode[STIX]{x1D719}$ for which these curves have an irreducible component of genus at most 1, and show that such 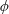$\unicode[STIX]{x1D719}$ must have two distinct iterates that are equal in 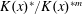$K(x)^{\ast }/K(x)^{\ast m}$.

Keywords

arithmetic dynamicsiteration of rational functionsspecial orbits of rational functiongenus of variables-separated curveLattès map

MSC classification

Primary: 37P05: Polynomial and rational maps
Secondary: 11G05: Elliptic curves over global fields 37P15: Global ground fields
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 4 , August 2019 , pp. 773 - 817
Copyright
© Canadian Mathematical Society 2018 

Footnotes

Authors J. C. and J. S. research was supported by Carleton College’s HHMI grant for undergraduate science education and the Carleton College department of Mathematics and Statistics.

References

An, T. T. H. and Diep, N. T. N., Genus one factors of curves defined by separated variable polynomials . J. Number Theory 133(2013), no. 8, 2616–2634. https://doi.org/10.1016/j.jnt.2012.12.017.Google Scholar
Avanzi, R. M. and Zannier, U. M., Genus one curves defined by separated variable polynomials and a polynomial Pell equation . Acta Arith. 99(2001), 227–256. https://doi.org/10.4064/aa99-3-2.Google Scholar
Avanzi, R. M. and Zannier, U. M., The equation f (X) = f (Y) in rational functions X = X (t), Y= Y (t) . Compositio Math. 139(2003), no. 3, 263–295. https://doi.org/10.1023/B:COMP.0000018136.23898.65.Google Scholar
Beardon, A. F., Iteration of rational functions. Complex analytic dynamical systems . Graduate Texts in Mathematics, 132, Springer-Verlag, New York, 1991. https://doi.org/10.1007/978-1-4612-4422-6.Google Scholar
Bell, J. P., Ghioca, D., and Tucker, T. J., The dynamical Mordell-Lang conjecture . Mathematical Surveys and Monographs, 210, American Mathematical Society, Providence, RI, 2016.Google Scholar
Bilu, Y. F. and Tichy, R. F., The Diophantine equation f (x) = g (y) . Acta Arith. 95(2000), no. 3, 261–288. https://doi.org/10.4064/aa-95-3-261-288.Google Scholar
Cremona, J., The elliptic curve database for conductors to 130000 . In: Algorithmic number theory , Lecture Notes in Comput. Sci., 4076, Springer, Berlin, 2006, pp. 11–29. https://doi.org/10.1007/11792086_2.Google Scholar
Fried, M. D., Arithmetical properties of function fields. II. The generalized Schur problem . Acta Arith. 25(1973/74), 225–258. https://doi.org/10.4064/aa-25-3-225-258.Google Scholar
Ghioca, D., Tucker, T. J., and Zieve, M. E., Intersections of polynomials orbits, and a dynamical Mordell-Lang conjecture . Invent. Math. 171(2008), 463–483. https://doi.org/10.1007/s00222-007-0087-5.Google Scholar
Ghioca, D., Tucker, T. J., and Zieve, M. E., Linear relations between polynomial orbits . Duke Math. J. 161(2012), no. 7, 1379–1410. https://doi.org/10.1215/00127094-1598098.Google Scholar
Gratton, C., Nguyen, K., and Tucker, T. J., ABC implies primitive prime divisors in arithmetic dynamics . Bull. Lond. Math. Soc. 45(2013), 1194–1208. https://doi.org/10.1112/blms/bdt049.Google Scholar
Hindry, M. and Silverman, J. H., Diophantine geometry: an introduction . Graduate Texts in Mathematics, 201, Springer-Verlag, New York, 2000. https://doi.org/10.1007/978-1-4612-1210-2.Google Scholar
Karpilovsky, G., Topics in field theory . North-Holland Mathematics Studies, 155, Notas de Matemática [Mathematical Notes], 124, North-Holland Publishing Co., Amsterdam, 1989.Google Scholar
Lang, S., Number theory. III. Diophantine geometry . Encyclopaedia of Mathematical Sciences, 60, Springer-Verlag, Berlin, 1991.Google Scholar
Milnor, J., On Lattès maps . In: Dynamics on the Riemann sphere , Eur. Math. Soc., Zürich, 2006, pp. 9–43. https://doi.org/10.4171/011-1/1.Google Scholar
Northcott, D. G., Periodic points on an algebraic variety . Ann. of Math. (2) 51(1950), 167–177. https://doi.org/10.2307/1969504.Google Scholar
Pakovich, F., Algebraic curves A °l (x) - U (y) = 0 and arithmetic of orbits of rational functions. 2018. arxiv:1801.01985.Google Scholar
Pakovich, F., Algebraic curves P (x) - Q (y) = 0 and functional equations . Complex Var. Elliptic Equ. 56(2011), no. 1–4, 199–213. https://doi.org/10.1080/17476930903394838.Google Scholar
Ritt, J. F., Prime and composite polynomials . Trans. Amer. Math. Soc. 23(1922), no. 1, 51–66. https://doi.org/10.2307/1988911.Google Scholar
Schinzel, A., Selected topics on polynomials . University of Michigan Press, Ann Arbor, Mich., 1982.Google Scholar
Silverman, J. H., Integer points, Diophantine approximation, and iteration of rational maps . Duke Math. J. 71(1993), no. 3, 793–829. https://doi.org/10.1215/S0012-7094-93-07129-3.Google Scholar
Silverman, J. H., The arithmetic of dynamical systems . Graduate Texts in Mathematics, 241, Springer, New York, 2007. https://doi.org/10.1007/978-0-387-69904-2.Google Scholar
Stichtenoth, H., Algebraic function fields and codes . Second ed., Graduate Texts in Mathematics, 254, Springer-Verlag, Berlin, 2009.Google Scholar