Let X be a space with two metrics d1 and d2. Let S :(X, d1) → (X, d2) be continuous. We say S has the generalized pseudoorbit shadowing property with respect to the metrics d1 and d2 if for every 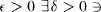every δ-pseudo-orbit in d1 can be ∊-shadowed by a true orbit in d2, i.e., if {x0, x1,…} satisfies 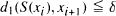for all i ≧ 0, then 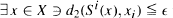for all i ≧ 0. The main result of this note shows that certain Markov operators P : L1→ L1 have the generalized shadowing property on weakly compact subsets of the space of probability density functions, where d1 is the metric of norm convergence and d2 is the metric of weak convergence. An important class of such operators are the Frobenius-Perron operators induced by certain expanding and nonexpanding maps on the interval. When there is exponential convergence of the iterates to the density, we can express δ in terms of ∊. We also show that, unlike the situation in the space X itself, the generalized shadowing property is valid for all parameters in families of maps and that there is stability of the shadowing property.