Article contents
Spectral Problems for Non-Linear Sturm-Liouville Equations with Eigenparameter Dependent Boundary Conditions
Published online by Cambridge University Press: 20 November 2018
Abstract
The nonlinear Sturm-Liouville equation
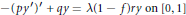 $$-{{\left( p{y}' \right)}^{\prime }}\,+\,qy\,=\,\text{ }\!\!\lambda\!\!\text{ }\left( 1-f \right)ry\,on\,[0,\,1]$$
$$-{{\left( p{y}' \right)}^{\prime }}\,+\,qy\,=\,\text{ }\!\!\lambda\!\!\text{ }\left( 1-f \right)ry\,on\,[0,\,1]$$
is considered subject to the boundary conditions
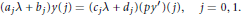 $$\left( {{\text{a}}_{j}}\text{ }\lambda \text{ }\text{+}{{\text{b}}_{j}} \right)y\left( j \right)=\left( {{c}_{j}}\text{ }\lambda \text{ }+{{d}_{j}} \right)\left( p{y}' \right)\left( j \right),j=0,1$$
$$\left( {{\text{a}}_{j}}\text{ }\lambda \text{ }\text{+}{{\text{b}}_{j}} \right)y\left( j \right)=\left( {{c}_{j}}\text{ }\lambda \text{ }+{{d}_{j}} \right)\left( p{y}' \right)\left( j \right),j=0,1$$
Here 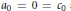 ${{\text{a}}_{0}}\,=\,0\,=\,{{c}_{0}}$ and
${{\text{a}}_{0}}\,=\,0\,=\,{{c}_{0}}$ and 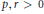 $p,\,r\,>\,0$ and
$p,\,r\,>\,0$ and 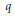 $q$ are functions depending on the independent variable
$q$ are functions depending on the independent variable 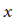 $x$ alone, while
$x$ alone, while 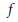 $f$ depends on
$f$ depends on 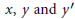 $x,\,y\,and\,{y}'$ . Results are given on existence and location of sets of
$x,\,y\,and\,{y}'$ . Results are given on existence and location of sets of 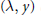 $(\lambda ,\,y)$ bifurcating from the linearized eigenvalues, and for which
$(\lambda ,\,y)$ bifurcating from the linearized eigenvalues, and for which 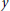 $y$ has prescribed oscillation count, and on completeness of the
$y$ has prescribed oscillation count, and on completeness of the 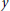 $y$ in an appropriate sense.
$y$ in an appropriate sense.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2000
References
- 8
- Cited by

