We study 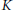 $K$ -orbits in
$K$ -orbits in 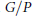 $G/P$ where
$G/P$ where 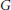 $G$ is a complex connected reductive group,
$G$ is a complex connected reductive group,  $P\,\subseteq \,G$ is a parabolic subgroup, and
$P\,\subseteq \,G$ is a parabolic subgroup, and 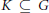 $K\,\subseteq \,G$ is the fixed point subgroup of an involutive automorphism
$K\,\subseteq \,G$ is the fixed point subgroup of an involutive automorphism 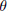 $\theta$ . Generalizing work of Springer, we parametrize the (finite) orbit set
$\theta$ . Generalizing work of Springer, we parametrize the (finite) orbit set 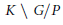 $K\,\backslash \,G/P$ and we determine the isotropy groups. As a consequence, we describe the closed (resp. affine) orbits in terms of
$K\,\backslash \,G/P$ and we determine the isotropy groups. As a consequence, we describe the closed (resp. affine) orbits in terms of 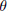 $\theta$ -stable (resp.
$\theta$ -stable (resp. 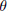 $\theta$ -split) parabolic subgroups. We also describe the decomposition of any
$\theta$ -split) parabolic subgroups. We also describe the decomposition of any 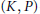 $(K,\,P)$ -double coset in
$(K,\,P)$ -double coset in 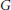 $G$ into
$G$ into 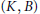 $(K,\,B)$ -double cosets, where
$(K,\,B)$ -double cosets, where 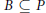 $B\,\subseteq \,P$ is a Borel subgroup. Finally, for certain
$B\,\subseteq \,P$ is a Borel subgroup. Finally, for certain 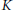 $K$ -orbit closures
$K$ -orbit closures 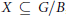 $X\,\subseteq \,G/B$ , and for any homogeneous line bundle
$X\,\subseteq \,G/B$ , and for any homogeneous line bundle 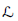 $\mathcal{L}$ on
$\mathcal{L}$ on 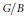 $G/B$ having nonzero global sections, we show that the restriction map
$G/B$ having nonzero global sections, we show that the restriction map 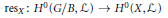 $\text{re}{{\text{s}}_{X}}\,:\,{{H}^{0}}\,\left( G\,/\,B,\,\mathcal{L} \right)\,\to \,{{H}^{0}}\,\left( X,\,\mathcal{L} \right)$ is surjective and that
$\text{re}{{\text{s}}_{X}}\,:\,{{H}^{0}}\,\left( G\,/\,B,\,\mathcal{L} \right)\,\to \,{{H}^{0}}\,\left( X,\,\mathcal{L} \right)$ is surjective and that 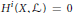 ${{H}^{i}}\,\left( X,\mathcal{L} \right)\,=\,0$ for
${{H}^{i}}\,\left( X,\mathcal{L} \right)\,=\,0$ for 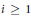 $i\,\ge \,1$ . Moreover, we describe the
$i\,\ge \,1$ . Moreover, we describe the 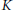 $K$ -module
$K$ -module 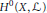 ${{H}^{0}}\left( X,L \right)$ . This gives information on the restriction to
${{H}^{0}}\left( X,L \right)$ . This gives information on the restriction to 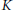 $K$ of the simple
$K$ of the simple 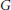 $G$ -module
$G$ -module 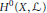 ${{H}^{0}}\,\left( G\,/\,B,\mathcal{L} \right)$ . Our construction is a geometric analogue of Vogan and Sepanski’s approach to extremal
${{H}^{0}}\,\left( G\,/\,B,\mathcal{L} \right)$ . Our construction is a geometric analogue of Vogan and Sepanski’s approach to extremal 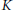 $K$ -types.
$K$ -types.
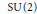 $\text{SU(2)}$ -Representations for Knot Complements and Cyclic Branched Covers
$\text{SU(2)}$ -Representations for Knot Complements and Cyclic Branched Covers
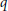 $q$ -Analogs of a Theorem of Kostant-Rallis
$q$ -Analogs of a Theorem of Kostant-Rallis