Hostname: page-component-cb9f654ff-9knnw Total loading time: 0 Render date: 2025-08-05T17:53:11.406Z Has data issue: false hasContentIssue false
  • English
  • Français

A dichotomy for topological full groups

Part of: Abstract harmonic analysis Topological dynamics

Published online by Cambridge University Press:  15 September 2022

Eduardo Scarparo Open the ORCID record for Eduardo Scarparo [Opens in a new window]
Eduardo Scarparo*
Affiliation:
School of Mathematics and Statistics, University of Glasgow, Glasgow, United Kingdom
*
e-mail: eduardo.scarparo@glasgow.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a minimal action 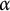$\alpha $ of a countable group on the Cantor set, we show that the alternating full group 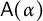$\mathsf {A}(\alpha )$ is non-amenable if and only if the topological full group 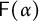$\mathsf {F}(\alpha )$ is 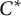$C^*$-simple. This implies, for instance, that the Elek–Monod example of non-amenable topological full group coming from a Cantor minimal 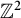$\mathbb {Z}^2$-system is 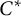$C^*$-simple.

Keywords

Topological full groupsC*-simplicityamenability

MSC classification

Primary: 43A07: Means on groups, semigroups, etc.; amenable groups
Secondary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)

Information

Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 2 , June 2023 , pp. 610 - 616
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No. 817597).

References

Bader, U., Duchesne, B., and Lécureux, J., Amenable invariant random subgroups . Israel J. Math. 213(2016), no. 1, 399–422, with an appendix by Phillip Wesolek.CrossRefGoogle Scholar
Breuillard, E., Kalantar, M., Kennedy, M., and Ozawa, N., ${C}^{\ast }$ -simplicity and the unique trace property for discrete groups . Publ. Math. Inst. Hautes Études Sci. 126(2017), 35–71.CrossRefGoogle Scholar
Brix, K. A. and Scarparo, E., ${{C}}^{\ast }$ -simplicity and representations of topological full groups of groupoids . J. Funct. Anal. 277(2019), no. 9, 2981–2996.CrossRefGoogle Scholar
Elek, G. and Monod, N., On the topological full group of a minimal Cantor ${\mathbf{Z}}^2$ -system . Proc. Amer. Math. Soc. 141(2013), no. 10, 3549–3552.CrossRefGoogle Scholar
Juschenko, K. and Monod, N., Cantor systems, piecewise translations and simple amenable groups . Ann. of Math. (2) 178 (2013), no. 2, 775–787.CrossRefGoogle Scholar
Kennedy, M., An intrinsic characterization of ${C}^{\ast }$ -simplicity . Ann. Sci. Éc. Norm. Supér. (4) 53(2020), no. 5, 1105–1119.CrossRefGoogle Scholar
Kerr, D. and Tucker-Drob, R., Dynamical alternating groups, stability, property Gamma, and inner amenability. Preprint, 2019. arXiv:1902.04131Google Scholar
Le Boudec, A. and Matte Bon, N., Subgroup dynamics and ${C}^{\ast }$ -simplicity of groups of homeomorphisms . Ann. Sci. Éc. Norm. Supér. (4) 51(2018), no. 3, 557–602.CrossRefGoogle Scholar
Li, X., Dynamic characterizations of quasi-isometry and applications to cohomology . Algebr. Geom. Topol. 18(2018), no. 6, 3477–3535.CrossRefGoogle Scholar
Matte Bon, N., Rigidity properties of full groups of pseudogroups over the Cantor set. Preprint, 2018. arXiv:1801.10133 Google Scholar
Matui, H., Some remarks on topological full groups of Cantor minimal systems . Internat. J. Math. 17(2006), no. 2, 231–251.CrossRefGoogle Scholar
Matui, H., Homology and topological full groups of étale groupoids on totally disconnected spaces . Proc. Lond. Math. Soc. (3) 104(2012), no. 1, 27–56.CrossRefGoogle Scholar
Matui, H., Topological full groups of one-sided shifts of finite type . J. Reine Angew. Math. 705(2015), 35–84.CrossRefGoogle Scholar
Nekrashevych, V., Simple groups of dynamical origin . Ergodic Theory Dynam. Systems 39(2019), no. 3, 707–732.CrossRefGoogle Scholar
Nyland, P. and Ortega, E., Topological full groups of ample groupoids with applications to graph algebras . Internat. J. Math. 30(2019), no. 4, 66, Article ID 1950018.CrossRefGoogle Scholar