Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Schmidt, Simon
2018.
The Petersen graph has no quantum symmetry.
Bulletin of the London Mathematical Society,
Vol. 50,
Issue. 3,
p.
395.
Lupini, Martino
Mančinska, Laura
and
Roberson, David E.
2020.
Nonlocal games and quantum permutation groups.
Journal of Functional Analysis,
Vol. 279,
Issue. 5,
p.
108592.
Junk, Luca
Schmidt, Simon
and
Weber, Moritz
2020.
Almost all trees have quantum symmetry.
Archiv der Mathematik,
Vol. 115,
Issue. 4,
p.
367.
Mancinska, Laura
and
Roberson, David E.
2020.
Quantum isomorphism is equivalent to equality of homomorphism counts from planar graphs.
p.
661.
Brannan, Michael
Eifler, Kari
Voigt, Christian
and
Weber, Moritz
2022.
Quantum Cuntz-Krieger algebras.
Transactions of the American Mathematical Society, Series B,
Vol. 9,
Issue. 26,
p.
782.
Levandovskyy, Viktor
Eder, Christian
Steenpass, Andreas
Schmidt, Simon
Schanz, Julien
and
Weber, Moritz
2022.
Existence of Quantum Symmetries for Graphs on Up to Seven Vertices.
p.
311.
Weber, Moritz
2023.
Quantum Permutation Matrices.
Complex Analysis and Operator Theory,
Vol. 17,
Issue. 3,
Razavinia, Farrokh
and
Haghighatdoost, Ghorbanali
2023.
From Quantum Automorphism of (Directed) Graphs to the Associated Multiplier Hopf Algebras.
Mathematics,
Vol. 12,
Issue. 1,
p.
128.
Nechita, Ion
Schmidt, Simon
and
Weber, Moritz
2023.
Sinkhorn Algorithm for Quantum Permutation Groups.
Experimental Mathematics,
Vol. 32,
Issue. 1,
p.
156.
Karmakar, Ujjal
and
Mandal, Arnab
2024.
Rigidity on quantum symmetry for a certain class of graph C*-algebras.
Journal of Mathematical Physics,
Vol. 65,
Issue. 8,
Bhattacharjee, Suvrajit
Joardar, Soumalya
and
Roy, Sutanu
2024.
Braided quantum symmetries of graph C∗-algebras.
International Journal of Mathematics,
Vol. 35,
Issue. 13,
Joardar, Soumalya
Rahaman, Atibur
and
Sharma, Jitender
2025.
Quantum isomorphism of 2-graphs.
International Journal of Mathematics,
Vol. 36,
Issue. 03,
Karmakar, Ujjal
and
Mandal, Arnab
2025.
Quantum symmetries of graph C∗-algebras having maximal permutational symmetry.
International Journal of Mathematics,
Vol. 36,
Issue. 10,
Bhattacharjee, Suvrajit
and
Joardar, Soumalya
2025.
Equivariant
$\textrm {C}^*$
-correspondences and compact quantum group actions on Pimsner algebras.
Canadian Journal of Mathematics,
Vol. 77,
Issue. 1,
p.
57.
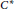 ${{C}^{*}}$ -algebras has a long history in operator algebras. Surprisingly, their quantum symmetries have not yet been computed. We close this gap by proving that the quantum automorphism group of a finite, directed graph without multiple edges acts maximally on the corresponding graph
${{C}^{*}}$ -algebras has a long history in operator algebras. Surprisingly, their quantum symmetries have not yet been computed. We close this gap by proving that the quantum automorphism group of a finite, directed graph without multiple edges acts maximally on the corresponding graph 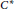 ${{C}^{*}}$ -algebra. This shows that the quantum symmetry of a graph coincides with the quantum symmetry of the graph
${{C}^{*}}$ -algebra. This shows that the quantum symmetry of a graph coincides with the quantum symmetry of the graph 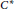 ${{C}^{*}}$ -algebra. In our result, we use the definition of quantum automorphism groups of graphs as given by Banica in 2005. Note that Bichon gave a different definition in 2003; our action is inspired from his work. We review and compare these two definitions and we give a complete table of quantum automorphism groups (with respect to either of the two definitions) for undirected graphs on four vertices.
${{C}^{*}}$ -algebra. In our result, we use the definition of quantum automorphism groups of graphs as given by Banica in 2005. Note that Bichon gave a different definition in 2003; our action is inspired from his work. We review and compare these two definitions and we give a complete table of quantum automorphism groups (with respect to either of the two definitions) for undirected graphs on four vertices.
