Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-28T05:55:22.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Co-maximal Graphs of Subgroups of Groups

Published online by Cambridge University Press:  20 November 2018

Saieed Akbari ,
Babak Miraftab  and
Reza Nikandish
Saieed Akbari
Affiliation:
Department of Mathematical Sciences, Sharif University of Technology, Tehran, Iran e-mail: s_akbari@sharif.edu e-mail: babak.math@gmail.com
Babak Miraftab
Affiliation:
Department of Mathematical Sciences, Sharif University of Technology, Tehran, Iran e-mail: s_akbari@sharif.edu e-mail: babak.math@gmail.com
Reza Nikandish
Affiliation:
Department of Basic Sciences, Jundi-Shapur University of Technology, Dezful, Iran e-mail: r.nikandish@ipm.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 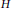$H$ be a group. The co-maximal graph of subgroups of 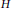$H$, denoted by 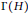$\Gamma \left( H \right)$, is a graph whose vertices are non-trivial and proper subgroups of 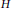$H$ and two distinct vertices $L$ and 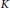$K$ are adjacent in 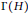$\Gamma \left( H \right)$ if and only if 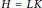$H\,=\,LK$. In this paper, we study the connectivity, diameter, clique number, and vertex chromatic number of 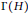$\Gamma \left( H \right)$. For instance, we show that if 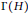$\Gamma \left( H \right)$ has no isolated vertex, then 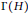$\Gamma \left( H \right)$ is connected with diameter at most 3. Also, we characterize all finitely groups whose co-maximal graphs are connected. Among other results, we show that if 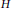$H$ is a finitely generated solvable group and 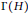$\Gamma \left( H \right)$ is connected, and moreover, the degree of a maximal subgroup is finite, then 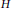$H$ is finite. Furthermore, we show that the degree of each vertex in the co-maximal graph of a general linear group over an algebraically closed field is zero or infinite.

Keywords

05C2505E1520D1020D15co-maximal graphs of subgroups of groupsdiameternilpotent groupsolvable group
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 1 , 01 March 2017 , pp. 12 - 25
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Abdollahi, A., Akbari, S., and Maimani, H. R., Non-commuting graph of a group. J. Algebra 298(2006), 468–492. http://dx.doi.Org/10.1016/j.jalgebra.2006.02.015 Google Scholar
[2] Afkhami, M. and Khashyarmanesh, K., The co-maximal graph of a lattice. Bull. Malays. Math.Sci. Soc 37(2014), 261–269.Google Scholar
[3] Akbari, S., Habibi, M., Majidinya, A., and Manaviyat, R., A note on co-maximal graph of non-commutative rings. Algebras and Representation Theory 16(2013), 303–307. http://dx.doi.Org/1 0.1007/s10468-011 -9309-z Google Scholar
[4] Akbari, S. and Mahdavi-Hezavehi, M., Some special subgroups of GLn(D). Algebra Colloq. 5(1998), 361–370.Google Scholar
[5] Akbari, S. and Mahdavi-Hezavehi, M., Normal subgroups of GLn(D) are not finitely generated. Proc. Amer. Math. Soc. 128(2000), no. 6, 1627–1632. http://dx.doi.Org/10.1090/S0002-9939-99-05182-5 Google Scholar
[6] Akbari, S., Miraftab, B., and Nikandish, R., A note on co-maximal ideal graph of commutative rings. Ars Combin., to appear.Google Scholar
[7] Akbari, S. and Nikandish, R., Some results on the intersection graphs of ideals of matrix algebras. Linear Multilinear Algebra 62(2014), 195–206. http://dx.doi.Org/10.1080/03081087.2013.769101 Google Scholar
[8] Akbari, S., Nikandish, R., and Nikmehr, M.J., Some results on the intersection graphs of ideals of rings. J. Algebra Appl. 12(2013), no. 4. http://dx.doi.Org/10.1142/S0219498812502003 Google Scholar
[9] Ballester-Bolinches, A. and Guo, X., On complemented subgroups of finite groups. Arch. Math. (Basel) 72(1999), no. 3. 161–166. http://dx.doi.Org/10.1007/s000130050317 Google Scholar
[10] Câlugâreanu, G., Breaz, S., Modoi, C., Pelea, C., and Vâlcan, D., Exercises in abelian group theory. Kluwer Academic Publishers, 2003.Google Scholar
[11] Hall, P., Complemented groups. J. London Math. Soc. 12 (1937), 201–204. http://dx.doi.Org/10.1112/jlms/s1-12.2.201 Google Scholar
[12] Hungerford, T. W., Algebra. Graduate Texts in Mathematics 73, Springer-Verlag, New York, 1980.Google Scholar
[13] Johnson, P. M., A property of factorizable groups. Arch. Math. (Basel) 60(1993), 414–419. http://dx.doi.Org/10.1007/BF01202304 Google Scholar
[14] Kappe, L.-C. and Kirtland, J., Supplementation in groups. Glasgow Math. J. 42(2000), 37–50. http://dx.doi.Org/10.1017/S0017089500010065 Google Scholar
[15] Moconja, S. M. and Petrovic, Z. Z., On the structure of co-maximal graphs of commutative rings with identity. Bull. Aust. Math. Soc. 83(2011), 11–21. http://dx.doi.Org/10.101 7/S0004972710001875 Google Scholar
[16] OFshanskii, A. Y., Geometry of defining relations in groups. Kluwer, 1991.Google Scholar
[17] Scott, W. R., Group theory. Dover Publications, New York, 1987.Google Scholar
[18] Sharma, P. D. and Bhatwadekar, S. M., A note on graphical representation of rings. J. Algebra 176(1995), 124–127. http://dx.doi.Org/10.1006/jabr.1995.1236 Google Scholar
[19] Suzuki, M., Group theory, I. Springer-Verlag, Berlin, 1982.Google Scholar
[20] Wang, H. J., Graphs associated to co-maximal ideals of commutative rings. J. Algebra 320(2008), 2917–2933. http://dx.doi.Org/10.1016/j.jalgebra.2008.06.020 Google Scholar
[21] Wang, H. J., Co-maximal graph of non-commutative rings. Linear Algebra and Appl. 430(2009), 633–641. http://dx.doi.Org/10.1016/j.laa.2008.08.026 Google Scholar
[22] Ye, M. and Wu, T., Co-maximal ideal graphs of commutative rings. J. Algebra Appl. 11(2012), no. 6. http://dx.doi.Org/1 0.1142/S021 9498812 501149 Google Scholar
[23] Zelinka, B., Intersection graphs of finite abelian groups. Czechoslovak Math. J. 25(1975), no. 2, 17–174.Google Scholar