Hostname: page-component-cb9f654ff-nr592 Total loading time: 0 Render date: 2025-08-10T22:22:35.916Z Has data issue: false hasContentIssue false
  • English
  • Français

Complemented Subspaces of Linear Bounded Operators

Published online by Cambridge University Press:  20 November 2018

Manijeh Bahreini ,
Elizabeth Bator  and
Ioana Ghenciu
Manijeh Bahreini
Affiliation:
University of Isfahan, Department of Mathematics, Isfahan 81745-163, Iran e-mail: mebahreini@math.ui.ac.ir
Elizabeth Bator
Affiliation:
University of North Texas, Department of Mathematics, Denton, Texas 76203-1430 e-mail: bator@unt.edu
Ioana Ghenciu
Affiliation:
University of Wisconsin–River Falls, Department of Mathematics, River Falls, WI 54022-5001 e-mail: ioana.ghenciu@uwrf.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the complementation of the space 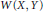$W\left( X,Y \right)$ of weakly compact operators, the space 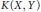$K\left( X,Y \right)$ of compact operators, the space 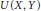$U\left( X,Y \right)$ of unconditionally converging operators, and the space 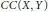$CC\left( X,Y \right)$ of completely continuous operators in the space 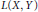$L\left( X,Y \right)$ of bounded linear operators from 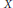$X$ to $Y$ . Feder proved that if 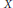$X$ is infinite-dimensional and 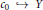${{c}_{0}}\,\to \,Y$ , then 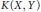$K\left( X,Y \right)$ is uncomplemented in 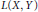$L\left( X,Y \right)$ . Emmanuele and John showed that if 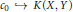${{c}_{0}}\,\to \,K(X,\,Y)$ , then 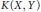$K\left( X,Y \right)$ is uncomplemented in 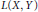$L\left( X,Y \right)$ . Bator and Lewis showed that if 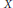$X$ is not a Grothendieck space and 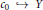${{c}_{0}}\,\to \,Y$ , then 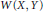$W\left( X,Y \right)$ is uncomplemented in 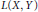$L\left( X,Y \right)$ . In this paper, classical results of Kalton and separably determined operator ideals with property 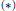$\left( * \right)$ are used to obtain complementation results that yield these theorems as corollaries.

Keywords

46B2046B28spaces of operatorscomplemented subspacescompact operatorsweakly compact operatorscompletely continuous operators

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 3 , 01 September 2012 , pp. 449 - 461
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Abott, C., Bator, E., Bilyeu, R., and Lewis, P., Weak precompactness, strong boundedness, and weak complete continuity. Math. Proc. Cambridge Philos. Soc. 108(1990), no. 2, 325–335. http://dx.doi.org/10.1017/S030500410006919X Google Scholar
[2] Arteburn, D. and Whitley, R., Projections in the space of bounded linear operators. Pacific J. Math. 15(1965), 739–746.Google Scholar
[3] Bator, E. and Lewis, P., Complemented spaces of operators. Bull. Polish Acad. Sci. Math. 50(2002), no. 4, 413–416.Google Scholar
[4] Bessaga, C. and Pełczyński, A., On bases and unconditional convergence of series in Banach spaces. Studia Math. 17(1958), 151–164.Google Scholar
[5] Brooks, J. K. and Lewis, P., Linear operators and vector measures. Trans. Amer. Math. Soc. 192(1974), 139–162. http://dx.doi.org/10.1090/S0002-9947-1974-0338821-5 Google Scholar
[6] Cembranos, P., Kalton, N., Saab, E., and Saab, P., Pełczyński's property (V) on C(Ω, E) spaces. Math. Ann. 271(1985), 91–97. http://dx.doi.org/10.1007/BF01455797 Google Scholar
[7] Diestel, J., Sequences and Series in Banach Spaces. Graduate Texts in Mathematics 92. Springer-Verlag, New York, 1984.Google Scholar
[8] Diestel, J., A survey of results related to the Dunford-Pettis property. In: Proceedings of the Conference on Integration, Topology, and Geometry in Linear Spaces. Contemp. Math. 2. American Mathematical Society, Providence, RI, 1980, pp. 15–60.Google Scholar
[9] Diestel, J. and Uhl, J. J. Jr., Vector Measures. Mathematical Surveys 15. American Mathematical Society, Providence, RI, 1977.Google Scholar
[10] Dobrakov, I., On representation of linear operators on C 0(T, X ). Czechoslovak. Math. J. 21(96)(1971), 13–30.Google Scholar
[11] Dunford, N. and Schwartz, J. T., Linear Operators. Part I: General Theory. John Wiley & Sons, New York, 1958.Google Scholar
[12] Emmanuele, G., A remark on the containment of c 0 in spaces of compact operators. Math. Proc. Cambridge Philos. Soc. 111(1992), no. 2, 331–335. http://dx.doi.org/10.1017/S0305004100075435 Google Scholar
[13] Emmanuele, G., Remarks on the uncomplemented subspace W(E, F). J. Funct. Anal. 99(1991), no. 1, 125–130. http://dx.doi.org/10.1016/0022-1236(91)90055-A Google Scholar
[14] Emmanuele, G., About the position of Kw* (X*, Y) inside Lw* (X*, Y). Atti Sem. Mat. Fis. Univ. Modena, 42(1994), no. 1, 123–133.Google Scholar
[15] Emmanuele, G. and John, K., Uncomplementability of spaces of compact operators in larger spaces of operators. Czechoslovak Math. J. 47(122)(1997), no. 1, 19–31. http://dx.doi.org/10.1023/A:1022483919972 Google Scholar
[16] Feder, M., On subspaces with an unconditional basis and spaces of operators. Illinois J. Math. 24(1980), no. 2, 196–205.Google Scholar
[17] Feder, M., On the nonexistance of a projection onto the space of compact operators. Canad. Math. Bull. 25(1982), no. 1, 78–81. http://dx.doi.org/10.4153/CMB-1982-011-0 Google Scholar
[18] Ghenciu, I. and Lewis, P., Strong Dunford-Pettis sets and spaces of operators. Monatsh. Math. 144(2005), no. 4, 275–284. http://dx.doi.org/10.1007/s00605-004-0295-7 Google Scholar
[19] Ghenciu, I. and Lewis, P., Tensor products and Dunford-Pettis sets. Math. Proc. Cambridge Philos. Soc. 139(2005), no. 2, 361–369. http://dx.doi.org/10.1017/S0305004105008558 Google Scholar
[20] Ghenciu, I. and Lewis, P., The embeddability of c 0 in spaces of operators. Bull. Polish Acad. Sci. Math. 56(2008), no. 3-4, 239–256. http://dx.doi.org/10.4064/ba56-3-7 Google Scholar
[21] Ghenciu, I. and Lewis, P., Dunford-Pettis properties and spaces of operators. Canad. Math. Bull. 52(2009), no. 2, 213–223. http://dx.doi.org/10.4153/CMB-2009-024-5 Google Scholar
[22] Ghenciu, I. and Lewis, P., The Dunford-Pettis property, the Gelfand-Phillips property and (L)-sets. Colloq. Math. 106(2006), no. 2, 311–324. http://dx.doi.org/10.4064/cm106-2-11 Google Scholar
[23] John, K., On the uncomplemented subspace K(X, Y). Czechoslovak Math. J. 42(117)(1992), no. 1, 167–173.Google Scholar
[24] Kalton, N., Spaces of compact operators. Math. Ann. 208(1974), 267–278. http://dx.doi.org/10.1007/BF01432152 Google Scholar
[25] Lewis, P., Spaces of operators and c 0 Studia Math. 145(2001), no. 3, 213–218. http://dx.doi.org/10.4064/sm145-3-3 Google Scholar
[26] Pełczyński, A., Banach spaces on which every unconditionally converging operator is weakly compact. Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys. 10(1962), 641–648.Google Scholar
[27] Rosenthal, H., On relatively disjoint families of measures, with some applications to Banach space theory. Studia Math. 37(1970), 13–36.Google Scholar
[28] Saab, E. and Saab, P., A stability property of a class of Banach spaces not containing a complemented copy of ℓ1. Proc. Amer. Math. Soc. 84(1982), no. 1, 44–46.Google Scholar
[29] Thorp, E., Projections onto the space of compact operators. Pacific J. Math. 10(1960), 693–696.Google Scholar
[30] Schlumprecht, T., Limited Sets in Banach Spaces. Dissertation, Munich, 1987.Google Scholar
[31] Ülger, A., Continuous linear operators on C(K, X) and pointwise weakly precompact subsets of C(K, X). Math. Proc. Cambridge Philos. Soc. 111(1992), no. 1, 143–150. http://dx.doi.org/10.1017/S0305004100075228 Google Scholar