No CrossRef data available.
Article contents
A Computation with the Connes–Thom Isomorphism
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let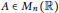 
$A\,\in \,{{M}_{n}}\left( \mathbb{R} \right)$ be an invertible matrix. Consider the semi-direct product 
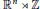${{\mathbb{R}}^{n}}\rtimes \,\mathbb{Z}$ where the action of 
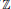$\mathbb{Z}$ on 
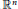${{\mathbb{R}}^{n}}$ is induced by the left multiplication by 
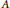$A$ . Let 
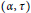$\left( \alpha ,\,\tau\right)$ be a strongly continuous action of 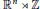${{\mathbb{R}}^{n}}\rtimes \,\mathbb{Z}$ on a 
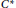${{C}^{*}}$ -algebra 
$B$ where 
$\alpha$ is a strongly continuous action of 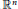${{\mathbb{R}}^{n}}$ and 
$\tau$ is an automorphism. The map $\tau$ induces a map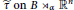 
$\widetilde{\tau }\,\text{on}\,\text{B}\,{{\rtimes }_{\alpha }}\,{{\mathbb{R}}^{n}}$ . We show that, at the 
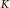$K$ -theory level, $\tau$ commutes with the Connes–Thom map if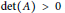 
$\det \left( A \right)\,>\,0$ and anticommutes if 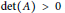$\det \left( A \right)\,>\,0$ . As an application, we recompute the 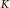$K$ -groups of the Cuntz–Li algebra associated with an integer dilation matrix.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2015
References
[1]
Boava, G. and Exel, R., Partial crossed product description of the C*-algebras associated with integral domains.
Proc. Amer. Math. Soc.
141(2013), no. 7, 2439-2451. http://dx.doi.Org/10.1090/S0002-9939-2013-11724-7
Google Scholar
[3]
Cuntz, J. and Li, X., K-theory of ring C* -algebras associated to function fields. arxiv:0911.5023Google Scholar
[4]
Cuntz, J. and Li, X., The regular C* -algebra of an integral domain. In: Quanta of maths, Clay Math. Proc, 11, American Mathematical Society, Providence, RI, 149–170.Google Scholar
[5]
Cuntz, J. and Li, X., C* -algebras associated with integral domains and crossed products by actions on adele spaces.
J. Noncommut. Geom.
5(2011), no. 1,1-37. http://dx.doi.Org/10.4171/JNCC/68
Google Scholar
[6]
Cuntz, J., C*-algebras associated with the ax + b-semigroup over N. In: Jf-theory and noncommutative geometry, EMS Ser. Congr. Rep., 2008, pp. 201–215.Google Scholar
[7]
Cuntz, J. and Vershik, A., C*-algebras associated with endomorphisms and polymorphsims of compact abelian groups.
Comm. Math. Phys.
321(2013), no. 1,157-179. http://dx.doi.Org/10.1007/s00220-012-1647-0
Google Scholar
[8]
Exel, R., an Huef, A., and Raeburn, I., Purely infinite simple C*-algebras associated to integer dilation matrices.
Indiana Univ. Math. J.
60(2011), no. 3,1033-1058. http://dx.doi.Org/10.1512/iumj.2011.60.4331
Google Scholar
[9]
Pack, T. and Skandalis, G., Connes’ analogue of the Thorn isomorphism for the Kasparov groups.
Invent. Math.
64(1981), no. 1, 7–14. http://dx.doi.Org/10.1007/BF01393931
Google Scholar
[10]
Kaliszewski, S., Landstad, M. B., and Quigg, J., A crossed-product approach to the Cuntz-Li algebras.
Proc. Edinb. Math. Soc. (2)
55(2012), no. 2, 429–459. http://dx.doi.Org/10.1017/S0013091511000046
Google Scholar
[11]
Li, X. and Luck, W., K-theoryfor ring
C*-algebras: the case of number fields with higher roots of unity. J. Topol. Anal.
4(2012), no. 4, 447–479. http://dx.doi.Org/10.1142/S1793525312500203
Google Scholar
[12]
Laca, M., Raeburn, I., and Ramagge, J., Phase transition on Exel crossed products associated to dilation matrices.
J. Funct. Anal.
261(2011), no. 12, 3633–3664. http://dx.doi.Org/10.1016/j.jfa.2O11.08.015
Google Scholar
[13]
Sundar, S., Cuntz-Li relations, inverse semigroups and groupoids.
Munster J. of Math.
5(2012), 151–182.Google Scholar
You have
Access