Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-27T05:37:31.611Z Has data issue: false hasContentIssue false
  • English
  • Français

The degree one Laguerre–Pólya class and the shuffle-word-embedding conjecture

Part of: Zeta and $L$-functions: analytic theory Holomorphic functions of several complex variables Linear function spaces and their duals Selfadjoint operator algebras

Published online by Cambridge University Press:  28 February 2024

James E. Pascoe Open the ORCID record for James E. Pascoe [Opens in a new window]  and
Hugo J. Woerdeman Open the ORCID record for Hugo J. Woerdeman [Opens in a new window]
James E. Pascoe
Affiliation:
Department of Mathematics, Drexel University, 3141 Chestnut Street, Philadelphia, PA 19104, United States e-mail: jep362@drexel.edu
Hugo J. Woerdeman*
Affiliation:
Department of Mathematics, Drexel University, 3141 Chestnut Street, Philadelphia, PA 19104, United States e-mail: jep362@drexel.edu
*
e-mail: hjw27@drexel.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We discuss the class of functions, which are well approximated on compacta by the geometric mean of the eigenvalues of a unital (completely) positive map into a matrix algebra or more generally a type 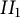$II_1$ factor, using the notion of a Fuglede–Kadison determinant. In two variables, the two classes are the same, but in three or more noncommuting variables, there are generally functions arising from type 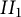$II_1$ von Neumann algebras, due to the recently established failure of the Connes embedding conjecture. The question of whether or not approximability holds for scalar inputs is shown to be equivalent to a restricted form of the Connes embedding conjecture, the so-called shuffle-word-embedding conjecture.

Keywords

Radical Laguerre–Pólya classBMV polynomialsConnes embedding conjectureshuffle-word-embedding conjecture

MSC classification

Primary: 46L54: Free probability and free operator algebras 46L52: Noncommutative function spaces 32A70: Functional analysis techniques 46E22: Hilbert spaces with reproducing kernels (= 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 8
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

J.E.P. was supported by the National Science Foundation grant DMS 2319010. H.J.W. was supported by the National Science Foundation grant DMS 2000037.

References

Bessis, D., Moussa, P., and Villani, M., Monotonic converging variational approximations to the functional integrals in quantum statistical mechanics . J. Math. Phys. 16(1975), no. 11, 2318–2325.CrossRefGoogle Scholar
Burgdorf, S., Dykema, K., Klep, I., and Schweighofer, M., Addendum to “Connes’ embedding conjecture and sums of Hermitian squares” [Adv. Math. 217 (4) (2008) 1816–1837] . Adv. Math. 252(2014), 805–811.CrossRefGoogle Scholar
Conway, J. B., A course in operator theory, Graduate Studies in Mathematics, 21, American Mathematical Society, Providence, RI, 2000.Google Scholar
Eremenko, A., Herbert Stahl’s proof of the BMV conjecture . Sb. Math. 206(2015), no. 1, 97–102.CrossRefGoogle Scholar
Grinshpan, A., Kaliuzhnyi-Verbovetskyi, D. S., Vinnikov, V., and Woerdeman, H. J., Stable and real zero polynomials in two variables . Multidim. Syst. Signal Proc. 27(2016), 1–26.CrossRefGoogle Scholar
Hanselka, C., Characteristic polynomials of symmetric matrices over the univariate polynomial ring . J. Algebra 487(2017), 340–356.CrossRefGoogle Scholar
Helton, J. W. and Vinnikov, V., Linear matrix inequality representation of sets . Comm. Pure Appl. Math. 60(2007), no. 5, 654–674.CrossRefGoogle Scholar
Ji, Z., Natarajan, A., Vidick, T., Wright, J., and Yuen, H., MIP*=RE . Comm. ACM 64(2021), no. 11, 131–138 CrossRefGoogle Scholar
Klep, I. and Schweighofer, M., Connes’ embedding conjecture and sums of Hermitian squares . Adv. Math. 217(2008), no. 4, 1816–1837.CrossRefGoogle Scholar
Klep, I. and Špenko, Š., A tracial Nullstellensatz . Bull. Lond. Math. Soc. 46(2014), no. 5, 1091–1098.CrossRefGoogle Scholar
Pascoe, J. E., Trace minmax functions and the radical Laguerre-Pólya class . Res. Math. Sci. 8(2021), no. 1, Article no. 9, 13 pp.CrossRefGoogle Scholar
Plaumann, D. and Vinzant, C., Determinantal representations of hyperbolic plane curves: An elementary approach . J. Symbolic Comput. 57(2013), 48–60.CrossRefGoogle Scholar
Stahl, H. R., Proof of the BMV conjecture . Acta Math. 211(2013), 255–290.CrossRefGoogle Scholar
Szász, O., On sequences of polynomials and the distribution of their zeros . Bull. Amer. Math. Soc. 49(1943), 377–380.CrossRefGoogle Scholar
Szegö, G., Orthogonal polynomials. 4th ed., American Mathematical Society, Providence, RI, 1978.Google Scholar