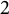Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-06-01T14:11:53.590Z Has data issue: false hasContentIssue false
  • English
  • Français

A dynamical characterization for monogenity at every level of some infinite $2$-towers

Part of: Algebraic number theory: global fields Multiplicative number theory

Published online by Cambridge University Press:  20 October 2021

Marianela Castillo
Marianela Castillo*
Affiliation:
Departamento de Ciencias Básicas, Universidad de Concepción, Campus Los Ángeles, Juan Antonio Coloma 201, Los Ángeles 4430000, Chile
*
e-mail: mcastillo@udec.cl
Get access Rights & Permissions [Opens in a new window]

Abstract

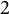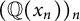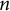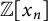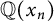We consider a concrete family of $2$ -towers $(\mathbb {Q}(x_n))_n$ of totally real algebraic numbers for which we prove that, for each $n$ , $\mathbb {Z}[x_n]$ is the ring of integers of $\mathbb {Q}(x_n)$ if and only if the constant term of the minimal polynomial of 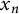$x_n$ is square-free. We apply our characterization to produce new examples of monogenic number fields, which can be of arbitrary large degree under the ABC-Conjecture.

Keywords

Totally real fields2-towersmonogenic fieldssquare-free integersiteration of polynomials

MSC classification

Primary: 11N32: Primes represented by polynomials; other multiplicative structure of polynomial values
Secondary: 11R04: Algebraic numbers; rings of algebraic integers 11R80: Totally real fields
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 3 , September 2022 , pp. 806 - 814
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The work is part of my PhD thesis [1] under the supervision of X. Vidaux and C. R. Videla, to whom I am grateful for support and encouragement. It has been supported by the Conicyt fellowship “Beca Doctorado Nacional,” by the Universidad de Concepción (Chile), and by the Fondecyt research project 1130134 (Chile) of X. Vidaux. Part of this work was done while visiting Carlos R. Videla at Mount Royal University, Calgary, Canada. I am grateful to the referees for their careful reading of this paper, which helped improving the presentation and simplify some proofs.

References

Castillo, M., On the Julia Robinson number of rings of totally real algebraic integers in some towers of nested square roots. Ph.D. thesis, Universidad de Concepción, Chile, 2018. http://dmat.cfm.cl/dmat/doctorado/tesis/Google Scholar
Gaál, I., Diophantine equations and power integral bases: theory and algorithms, Birkhäuser, Boston, 2002.10.1007/978-1-4612-0085-7CrossRefGoogle Scholar
Granville, A., ABC allows us to count squarefrees , Int. Math. Res. Not. IMRN 1998(1998), no. 19, 991–1009.10.1155/S1073792898000592CrossRefGoogle Scholar
Liang, J. J., On the integral basis of the maximal real subfield of a cyclotomic field . J. Reine Angew. Math. 286−287(1976), 223–226.Google Scholar
Marcus, D., Number fields, Springer-Verlag, New York, 1977.10.1007/978-1-4684-9356-6CrossRefGoogle Scholar
Narkiewicz, W., Elementary and analytic theory of algebraic numbers, 3rd ed., Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2004, xii+708 p.10.1007/978-3-662-07001-7CrossRefGoogle Scholar
Serre, J.-P., Lectures on the Mordell−Weil theorem, Aspects of Mathematics, E15, Friedr. Vieweg and Sohn, Braunschweig, 1989, x+218 p. Translated from the French and edited by Martin Brown from notes by Michel Waldschmidt.10.1007/978-3-663-14060-3CrossRefGoogle Scholar
Stoll, M., Galois group over $\ \mathbb{Q}\ {}$ of some iterated polynomials . Arch. Math. 59(1992), 239−244.10.1007/BF01197321CrossRefGoogle Scholar
Uchida, K., When is $\ Z\left[\alpha \right]\ {}$ the ring of the integers? Osaka J. Math. 14(1977), no. 1, 155–157.Google Scholar
Vidaux, X. and Videla, C. R., Definability of the natural numbers in totally real towers of nested square roots . Proc. Amer. Math. Soc. 143(2015), 4463–4477.10.1090/S0002-9939-2015-12592-0CrossRefGoogle Scholar