Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-29T15:36:19.469Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimates for generalized Bohr radii in one and higher dimensions

Part of: Series expansions Measures, integration, derivative, holomorphy Spaces and algebras of analytic functions Holomorphic functions of several complex variables Linear function spaces and their duals

Published online by Cambridge University Press:  04 November 2022

Nilanjan Das
Nilanjan Das*
Affiliation:
Theoretical Statistics and Mathematics Unit, Indian Statistical Institute Kolkata, Kolkata 700108, India
*
e-mail: nilanjand7@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we study a generalized Bohr radius 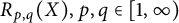$R_{p, q}(X), p, q\in [1, \infty )$ defined for a complex Banach space X. In particular, we determine the exact value of 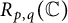$R_{p, q}(\mathbb {C})$ for the cases (i) 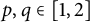$p, q\in [1, 2]$ , (ii) 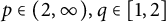$p\in (2, \infty ), q\in [1, 2]$ , and (iii) 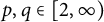$p, q\in [2, \infty )$ . Moreover, we consider an n-variable version 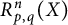$R_{p, q}^n(X)$ of the quantity 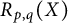$R_{p, q}(X)$ and determine (i) 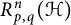$R_{p, q}^n(\mathcal {H})$ for an infinite-dimensional complex Hilbert space $\mathcal {H}$ and (ii) the precise asymptotic value of 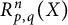$R_{p, q}^n(X)$ as 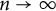$n\to \infty $ for finite-dimensional X. We also study the multidimensional analog of a related concept called the p-Bohr radius. To be specific, we obtain the asymptotic value of the n-dimensional p-Bohr radius for bounded complex-valued functions, and in the vector-valued case, we provide a lower estimate for the same, which is independent of n.

Keywords

Bohr radiusholomorphic functionsBanach spaces

MSC classification

Primary: 30B10: Power series (including lacunary series) 32A05: Power series, series of functions 46E40: Spaces of vector- and operator-valued functions
Secondary: 30H05: Bounded analytic functions 32A10: Holomorphic functions 32A17: Special families of functions 46G20: Infinite-dimensional holomorphy
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 2 , June 2023 , pp. 682 - 699
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author of this article is supported by a Research Associateship provided by the Stat-Math Unit of ISI Kolkata.

References

Aizenberg, L., Aytuna, A., and Djakov, P., An abstract approach to Bohr’s phenomenon . Proc. Amer. Math. Soc. 128(2000), no. 9, 2611–2619.CrossRefGoogle Scholar
Aizenberg, L. A., Grossman, I. B., Korobeĭnik, Yu. F., Some remarks on the Bohr radius for power series (in Russian) . Izv. Vyssh. Uchebn. Zaved. Mat. 46(2002), no. 10, 3–10; translation in Russian Math. (Iz. VUZ) 46(2002), no. 10, 1–8 (2003).Google Scholar
Balasubramanian, R., Calado, B., and Queffélec, H., The Bohr inequality for ordinary Dirichlet series . Studia Math. 175(2006), no. 3, 285–304.CrossRefGoogle Scholar
Bayart, F., Pellegrino, D., and Seoane-Sepúlveda, J. B., The Bohr radius of the $n$ -dimensional polydisk is equivalent to $\sqrt{(\log n)/ n}$ . Adv. Math. 264(2014), 726–746.CrossRefGoogle Scholar
Bénéteau, C., Dahlner, A., and Khavinson, D., Remarks on the Bohr phenomenon . Comput. Methods Funct. Theory 4(2004), no. 1, 1–19.CrossRefGoogle Scholar
Bhowmik, B. and Das, N., A characterization of Banach spaces with nonzero Bohr radius . Arch. Math. 116(2021), no. 5, 551–558.CrossRefGoogle Scholar
Bhowmik, B. and Das, N., On some aspects of the Bohr inequality . Rocky Mountain J. Math. 51(2021), no. 1, 87–96.CrossRefGoogle Scholar
Bhowmik, B. and Das, N., Bohr radius and its asymptotic value for holomorphic functions in higher dimensions . C. R. Math. Acad. Sci. Paris 359(2021), 911–918.Google Scholar
Blasco, O., The Bohr radius of a Banach space . In: Vector measures, integration and related topics, Operator Theory: Advances and Applications, 201, Birkhäuser, Basel, 2010, pp. 59–64.Google Scholar
Blasco, O., The $p$ -Bohr radius of a Banach space . Collect. Math. 68(2017), no. 1, 87–100.CrossRefGoogle Scholar
Blasco, O. and Pavlović, M., Complex convexity and vector-valued Littlewood–Paley inequalities . Bull. Lond. Math. Soc. 35(2003), no. 6, 749–758.CrossRefGoogle Scholar
Boas, H. P. and Khavinson, D., Bohr’s power series theorem in several variables . Proc. Amer. Math. Soc. 125(1997), no. 10, 2975–2979.CrossRefGoogle Scholar
Bohr, H., A theorem concerning power series . Proc. Lond. Math. Soc. 2(1914), no. 13, 1–5.CrossRefGoogle Scholar
Bombieri, E., Sopra un teorema di H. Bohr e G. Ricci sulle funzioni maggioranti delle serie di potenze (in Italian) . Boll. Un. Mat. Ital. 3(1962), no. 17, 276–282.Google Scholar
Defant, A., García, D., Maestre, M., and Pérez-García, D., Bohr’s strip for vector valued Dirichlet series . Math. Ann. 342(2008), no. 3, 533–555.CrossRefGoogle Scholar
Defant, A., García, D., Maestre, M., and Sevilla-Peris, P., Dirichlet series and holomorphic functions in high dimensions, New Mathematical Monographs, 37, Cambridge University Press, Cambridge, 2019.CrossRefGoogle Scholar
Defant, A., Maestre, M., and Schwarting, U., Bohr radii of vector valued holomorphic functions . Adv. Math. 231(2012), no. 5, 2837–2857.CrossRefGoogle Scholar
Diestel, J., Jarchow, H., and Tonge, A., Absolutely summing operators, Cambridge Studies in Advanced Mathematics, 43, Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Dixon, P. G., Banach algebras satisfying the non-unital von Neumann inequality . Bull. Lond. Math. Soc. 27(1995), no. 4, 359–362.CrossRefGoogle Scholar
Djakov, P. B. and Ramanujan, M. S., A remark on Bohr’s theorem and its generalizations . J. Anal. 8(2000), 65–77.Google Scholar
Galicer, D., Mansilla, M., and Muro, S., Mixed Bohr radius in several variables . Trans. Amer. Math. Soc. 373(2020), no. 2, 777–796.CrossRefGoogle Scholar
Globevnik, J., On complex strict and uniform convexity . Proc. Amer. Math. Soc. 47(1975), 175–178.CrossRefGoogle Scholar
Hamada, H., Honda, T., and Kohr, G., Bohr’s theorem for holomorphic mappings with values in homogeneous balls . Israel J. Math. 173(2009), 177–187.CrossRefGoogle Scholar
Hamada, H., Honda, T., and Mizota, Y., Bohr phenomenon on the unit ball of a complex Banach space . Math. Inequal. Appl. 23(2020), no. 4, 1325–1341.Google Scholar
Kayumov, I. R. and Ponnusamy, S., On a powered Bohr inequality . Ann. Acad. Sci. Fenn. Math. 44(2019), no. 1, 301–310.CrossRefGoogle Scholar
Lassère, P. and Mazzilli, E., Estimates for the Bohr radius of a Faber–Green condenser in the complex plane . Constr. Approx. 45(2017), no. 3, 409–426.CrossRefGoogle Scholar
Liu, M. S. and Ponnusamy, S., Multidimensional analogues of refined Bohr’s inequality . Proc. Amer. Math. Soc. 149(2021), no. 5, 2133–2146.CrossRefGoogle Scholar
Paulsen, V. I. and Singh, D., Bohr’s inequality for uniform algebras . Proc. Amer. Math. Soc. 132(2004), no. 12, 3577–3579.CrossRefGoogle Scholar
Popescu, G., Multivariable Bohr inequalities . Trans. Amer. Math. Soc. 359(2007), no. 11, 5283–5317.CrossRefGoogle Scholar
Popescu, G., Bohr inequalities for free holomorphic functions on polyballs . Adv. Math. 347(2019), 1002–1053.CrossRefGoogle Scholar