Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-29T01:23:19.333Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized torsion for knots with arbitrarily high genus

Part of: Low-dimensional topology

Published online by Cambridge University Press:  02 December 2021

Kimihiko Motegi Open the ORCID record for Kimihiko Motegi [Opens in a new window]  and
Masakazu Teragaito Open the ORCID record for Masakazu Teragaito [Opens in a new window]
Kimihiko Motegi
Affiliation:
Department of Mathematics, Nihon University, 3-25-40 Sakurajosui, Setagaya-ku, Tokyo, 156-8550, Japan e-mail: motegi.kimihiko@nihon-u.ac.jp
Masakazu Teragaito*
Affiliation:
Department of Mathematics and Mathematics Education, Hiroshima University, 1-1-1 Kagamiyama, Higashi-hiroshima, Hiroshima, 739-8524, Japan
*
e-mail: teragai@hiroshima-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a group, and let g be a nontrivial element in G. If some nonempty finite product of conjugates of g equals the identity, then g is called a generalized torsion element. We say that a knot K has generalized torsion if 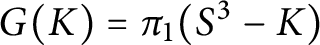$G(K) = \pi _1(S^3 - K)$ admits such an element. For a 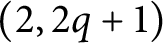$(2, 2q+1)$ -torus knot K, we demonstrate that there are infinitely many unknots 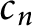$c_n$ in 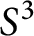$S^3$ such that p-twisting K about 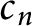$c_n$ yields a twist family 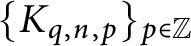$\{ K_{q, n, p}\}_{p \in \mathbb {Z}}$ in which 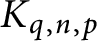$K_{q, n, p}$ is a hyperbolic knot with generalized torsion whenever 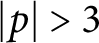$|p|> 3$ . This gives a new infinite class of hyperbolic knots having generalized torsion. In particular, each class contains knots with arbitrarily high genus. We also show that some twisted torus knots, including the 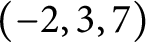$(-2, 3, 7)$ -pretzel knot, have generalized torsion. Because generalized torsion is an obstruction for having bi-order, these knots have non-bi-orderable knot groups.

Keywords

Fundamental groupDehn fillingslopegeneralized torsion

MSC classification

Secondary: 57M05: Fundamental group, presentations, free differential calculus 57M50: Geometric structures on low-dimensional manifolds
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 4 , December 2022 , pp. 867 - 881
Check for updates
Copyright
© Canadian Mathematical Society, 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dedicated to the memory of Toshie Takata. The first-named author has been partially supported by JSPS KAKENHI Grant Number 19K03502 and Joint Research Grant of the Institute of Natural Sciences at Nihon University for 2021. The second-named author has been supported by JSPS KAKENHI Grant Number 20K03587.

References

Baker, K. L. and Motegi, K., Twist families of L-space knots, their genera, and Seifert surgeries. Comm. Anal. Geom. 27(2019), 743–790.CrossRefGoogle Scholar
Boyer, S., Rolfsen, D., and Wiest, B., Orderable 3-manifold groups. Ann. Inst. Fourier 55(2005), 243–288.CrossRefGoogle Scholar
Christianson, K., Goluboff, J., Hamann, L., and Varadaraj, S., Non-left-orderable surgeries on twisted torus knots. Proc. Amer. Math. Soc. 144(2016), no. 6, 2683–2696.CrossRefGoogle Scholar
Clay, A. and Rolfsen, D., Ordered groups, eigenvalues, knots, surgery and L-spaces. Math. Proc. Cambridge Philos. Soc. 152(2012), no. 1, 115–129.CrossRefGoogle Scholar
Clay, A. and Watson, L., Left-orderable fundamental groups and Dehn surgery. Int. Math. Res. Not. IMRN. 12(2013), 2862–2890.CrossRefGoogle Scholar
Deruelle, A., Miyazaki, K., and Motegi, K., Networking Seifert surgeries on knots. Mem. Amer. Math. Soc. 217(2012), no. 1021, viii + 130.Google Scholar
Hironaka, E., The Lehmer polynomial and pretzel links. Canad. Math. Bull. 44(2001), 440–451.CrossRefGoogle Scholar
Hironaka, E. and Kin, E., A family of pseudo-Anosov braids with small dilatation. Algebr. Geom. Topol. 6(2006), 699–738.CrossRefGoogle Scholar
Howie, J. and Short, H., The band-sum problem. J. Lond. Math. Soc. 31(1985), 571–576.CrossRefGoogle Scholar
Johnson, J., Residual torsion-free nilpotence, bi-orderability and pretzel knots. Preprint, 2021. arXiv:2008.13353 Google Scholar
Kawauchi, A., Classification of pretzel knots. Kobe J. Math. 2(1985), no. 1, 11–22.Google Scholar
Kin, E. and Rolfsen, D., Braids, orderings, and minimal volume cusped hyperbolic 3-manifolds. Groups Geom. Dyn. 12(2018), no. 3, 961–1004.CrossRefGoogle Scholar
Lidman, T. and Moore, A., Pretzel knots with L-space surgeries. Michigan Math. J. 65(2016), no. 1, 105–130.CrossRefGoogle Scholar
Miyazaki, K. and Motegi, K., Seifert fibered manifolds and Dehn surgery III. Comm. Anal. Geom. 7(1999), 551–582.CrossRefGoogle Scholar
Motegi, K. and Teragaito, M., Generalized torsion elements and bi-orderability of 3-manifold groups. Canad. Math. Bull. 60(2017), 830–844.CrossRefGoogle Scholar
Mura, R. and Rhemtulla, A., Orderable groups, Lecture Notes in Pure and Applied Mathematics, 27, Marcel Dekker, Inc., New York–Basel, 1977.Google Scholar
Naylor, G. and Rolfsen, D., Generalized torsion in knot groups. Canad. Math. Bull. 59(2016), 182–189.CrossRefGoogle Scholar
Stallings, J. R., Constructions of fibered knots and links. Proc. Sympos. Pure Math. 32(1978), 55–60.CrossRefGoogle Scholar
Teragaito, M., Generalized torsion elements in the knot groups of twist knots. Proc. Amer. Math. Soc. 144(2016), no. 6, 2677–2682.CrossRefGoogle Scholar
Teragaito, M., Generalized torsion elements and hyperbolic links. J. Knot Theory Ramifications 29(2020), no. 11, 2050079.CrossRefGoogle Scholar