Hostname: page-component-5b777bbd6c-f9nfp Total loading time: 0 Render date: 2025-06-24T11:14:01.162Z Has data issue: false hasContentIssue false
  • English
  • Français

Helicoidal Minimal Surfaces in a Finsler Space of Randers Type

Published online by Cambridge University Press:  20 November 2018

Rosângela Maria da Silva  and
Keti Tenenblat
Rosângela Maria da Silva
Affiliation:
Instituto de Matemática e Estatística, IME—Universidade Federal de Goiás, 74001-970, Goiânia, GO, Brazil e-mail: rosams@ufg.br
Keti Tenenblat
Affiliation:
Departamento de Matemática, Universidade de Brasília, 70904-970, Brasília, DF, Brazil e-mail: keti@mat.unb.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the Finsler space 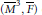$\left( {{\overline{M}}^{3}},\,\overline{F} \right)$ obtained by perturbing the Euclidean metric of 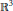${{\mathbb{R}}^{3}}$ by a rotation. It is the open region of 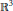${{\mathbb{R}}^{3}}$ bounded by a cylinder with a Randers metric. Using the Busemann–Hausdorff volume form, we obtain the differential equation that characterizes the helicoidal minimal surfaces in 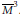${{\overline{M}}^{3}}$. We prove that the helicoid is a minimal surface in 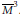${{\overline{M}}^{3}}$ only if the axis of the helicoid is the axis of the cylinder. Moreover, we prove that, in the Randers space 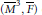$\left( {{\overline{M}}^{3}},\,\overline{F} \right)$, the only minimal surfaces in the Bonnet family with fixed axis 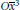$O{{\overline{x}}^{3}}$ are the catenoids and the helicoids.

Keywords

53A1053B40minimal surfaceshelicoidal surfacesFinsler spaceRanders space
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 4 , 01 December 2014 , pp. 765 - 779
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Bao, D., Chern, S. S., and Shen, Z., An introduction to Riemann-Finsler geometry. Graduate Texts in Mathematics, Springer-Verlag, New York, 2000.Google Scholar
[2] Bao, D., Robles, C., and Shen, Z., Zermelo navigation on Riemannian manifolds. J. Differential Geom. 66 (2004), no. 3, 377–435.Google Scholar
[3] Cui, N. and Shen, Y-B., Bernstein type theorems for minimal surfaces in-space. Publ. Math. Debrecen 74 (2009), no. 3–4, 383–400.Google Scholar
[4] Cui, N. and Shen, Y-B., Minimal rotational hypersurfaces in Minkowski-space. Geom. Dedicata 151 (2011), 27–39. http://dx.doi.org/10.1007/s10711-010-9517-4 Google Scholar
[5] He, Q. and Shen, Y.-B., On Bernstein type theorems in Finsler spaces with volume form induced from the projective sphere bundle. Proc. Amer. Math. Soc. 134 (2006), no. 3, 871–880. http://dx.doi.org/10.1090/S0002-9939-05-08017-2 Google Scholar
[6] Shen, Z., On Finsler geometry of submanifolds. Math. Ann. 311 (1998), no. 3, 549–576. http://dx.doi.org/10.1007/s002080050200 Google Scholar
[7] Shen, Z., Lectures on Finsler geometry. World Scientific Publishing, Singapore, 2001.Google Scholar
[8] Shen, Z., Finsler metrics with K= 0 and S = 0. Canad. J. Math. 55 (2003), no. 1, 112–132. http://dx.doi.org/10.4153/CJM-2003-005-6 Google Scholar
[9] M. da Silva and, R. Tenenblat, K., Minimal surfaces in a cylindrical region of R3 with a Randers metric. Houston J. Math. 37 (2011), no. 3, 745–771.Google Scholar
[10] Souza, M., Spruck, J., and Tenenblat, K., A Bernstein type theorem on a Randers space. Math. Ann. 329 (2004), no. 2, 291–305. http://dx.doi.org/10.1007/s00208-003-0500-3 Google Scholar
[11] Souza, M. and Tenenblat, K., Minimal surfaces of rotation in Finsler space with a Randers metric. Math. Ann. 325 (2003), no. 4, 625–642. http://dx.doi.org/10.1007/s00208-002-0392-7 Google Scholar
[12] Y.Wu, B., A local rigidity theorem for minimal surfaces in Minkowski 3-space of Randers type.Ann. Global Anal. and Geom. 31 (2007), no. 4, 375–384. http://dx.doi.org/10.1007/s10455-006-9046-4 Google Scholar