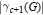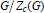Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ellis, Graham
and
McDermott, Aidan
1998.
Tensor products of prime-power groups.
Journal of Pure and Applied Algebra,
Vol. 132,
Issue. 2,
p.
119.
Salemkar, Ali Reza
Edalatzadeh, Behrouz
and
Araskhan, Mehdi
2009.
Some inequalities for the dimension of the c-nilpotent multiplier of Lie algebras.
Journal of Algebra,
Vol. 322,
Issue. 5,
p.
1575.
Araskhan, Mehdi
2013.
The dimension of the c -nilpotent multiplier.
Journal of Algebra,
Vol. 386,
Issue. ,
p.
105.
Rismanchian, Mohammad Reza
and
Araskhan, Mehdi
2014.
Some Properties of the c-Nilpotent Multiplier and c-Covers of Lie Algebras.
Algebra Colloquium,
Vol. 21,
Issue. 03,
p.
421.
NIROOMAND, PEYMAN
and
PARVIZI, MOHSEN
2015.
ON THE 2-NILPOTENT MULTIPLIER OF FINITEp-GROUPS.
Glasgow Mathematical Journal,
Vol. 57,
Issue. 1,
p.
201.
Casolo, Carlo
Dardano, Ulderico
and
Rinauro, Silvana
2016.
Variants of theorems of Baer and Hall on finite-by-hypercentral groups.
Journal of Algebra,
Vol. 452,
Issue. ,
p.
279.
Salemkar, Ali Reza
Talebtash, Sajedeh
and
Riyahi, Zahra
2017.
The nilpotent multipliers of crossed modules.
Journal of Pure and Applied Algebra,
Vol. 221,
Issue. 8,
p.
2119.
Jafari, S. Hadi
and
Hadizadeh, Halimeh
2020.
On the triple tensor product of prime-power groups.
Journal of Group Theory,
Vol. 23,
Issue. 5,
p.
879.
Niroomand, Peyman
Johari, Farangis
and
Parvizi, Mohsen
2020.
c-Nilpotent Multiplier of Finite p-Groups.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 43,
Issue. 1,
p.
941.
Johari, Farangis
Niroomand, Peyman
and
Parvizi, Mohsen
2020.
c-Nilpotent multiplier and c-capability of the direct sum of Lie algebras.
Journal of Algebra and Its Applications,
Vol. 19,
Issue. 02,
p.
2050037.
Donadze, Guram
and
García‐Martínez, Xabier
2021.
Some generalisations of Schur's and Baer's theorem and their connection with homological algebra.
Mathematische Nachrichten,
Vol. 294,
Issue. 11,
p.
2129.
Khamseh, E.
and
Hadi Jafari, S.
2024.
Computing the 2-nilpotent multiplier of 2-generator p-groups of class 2.
Indian Journal of Pure and Applied Mathematics,
Mahdipour, Fateme
and
Sanati, Mahboubeh Alizadeh
2025.
Polynilpotent multiplier of extra special P-groups.
Asian-European Journal of Mathematics,
Vol. 18,
Issue. 03,
Jafari, S. Hadi
and
Casas, J. M.
2025.
On the 2-nilpotent multipliers of p-groups with fixed coclass.
Ricerche di Matematica,