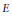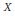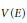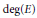Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Choe, Insong
Choy, Jaeyoo
and
Park, Seongsuk
2007.
Maximal line subbundles of stable bundles of rank 2 over an algebraic curve.
Geometriae Dedicata,
Vol. 125,
Issue. 1,
p.
191.