Article contents
Monoidal Categories, 2-Traces, and Cyclic Cohomology
Published online by Cambridge University Press: 07 January 2019
Abstract
In this paper we show that to a unital associative algebra object (resp. co-unital co-associative co-algebra object) of any abelian monoidal category (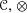 $\mathscr{C},\otimes$) endowed with a symmetric 2-trace, i.e., an
$\mathscr{C},\otimes$) endowed with a symmetric 2-trace, i.e., an 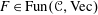 $F\in \text{Fun}(\mathscr{C},\text{Vec})$ satisfying some natural trace-like conditions, one can attach a cyclic (resp. cocyclic) module, and therefore speak of the (co)cyclic homology of the (co)algebra “with coefficients in
$F\in \text{Fun}(\mathscr{C},\text{Vec})$ satisfying some natural trace-like conditions, one can attach a cyclic (resp. cocyclic) module, and therefore speak of the (co)cyclic homology of the (co)algebra “with coefficients in 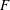 $F$”. Furthermore, we observe that if
$F$”. Furthermore, we observe that if 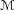 $\mathscr{M}$ is a
$\mathscr{M}$ is a 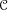 $\mathscr{C}$-bimodule category and
$\mathscr{C}$-bimodule category and 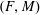 $(F,M)$ is a stable central pair, i.e.,
$(F,M)$ is a stable central pair, i.e.,  $F\in \text{Fun}(\mathscr{M},\text{Vec})$ and
$F\in \text{Fun}(\mathscr{M},\text{Vec})$ and 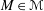 $M\in \mathscr{M}$ satisfy certain conditions, then
$M\in \mathscr{M}$ satisfy certain conditions, then 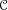 $\mathscr{C}$ acquires a symmetric 2-trace. The dual notions of symmetric 2-contratraces and stable central contrapairs are derived as well. As an application we can recover all Hopf cyclic type (co)homology theories.
$\mathscr{C}$ acquires a symmetric 2-trace. The dual notions of symmetric 2-contratraces and stable central contrapairs are derived as well. As an application we can recover all Hopf cyclic type (co)homology theories.
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
References
- 3
- Cited by

