Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-28T04:44:30.332Z Has data issue: false hasContentIssue false
  • English
  • Français

Norms on complex matrices induced by random vectors II: extension of weakly unitarily invariant norms

Part of: Basic linear algebra Rings with polynomial identity General theory of linear operators

Published online by Cambridge University Press:  06 November 2023

Ángel Chávez ,
Stephan Ramon Garcia  and
Jackson Hurley
Ángel Chávez*
Affiliation:
Mathematics Department, Regis University, 3333 Regis Boulevard, Denver, CO 80221 D-16, United States
Stephan Ramon Garcia
Affiliation:
Department of Mathematics and Statistics, Pomona College, 610 North College Avenue, Claremont, CA 91711, United States e-mail: stephan.garcia@pomona.edu jacksonwhurley@gmail.com
Jackson Hurley
Affiliation:
Department of Mathematics and Statistics, Pomona College, 610 North College Avenue, Claremont, CA 91711, United States e-mail: stephan.garcia@pomona.edu jacksonwhurley@gmail.com
*
e-mail: chave360@regis.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We improve and expand in two directions the theory of norms on complex matrices induced by random vectors. We first provide a simple proof of the classification of weakly unitarily invariant norms on the Hermitian matrices. We use this to extend the main theorem in Chávez, Garcia, and Hurley (2023, Canadian Mathematical Bulletin 66, 808–826) from exponent 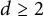$d\geq 2$ to 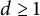$d \geq 1$. Our proofs are much simpler than the originals: they do not require Lewis’ framework for group invariance in convex matrix analysis. This clarification puts the entire theory on simpler foundations while extending its range of applicability.

Keywords

Normsymmetric polynomialtraceprobability distributionunitary invariance

MSC classification

Primary: 47A30: Norms (inequalities, more than one norm, etc.) 15A60: Norms of matrices, numerical range, applications of functional analysis to matrix theory 16R30: Trace rings and invariant theory
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

S.R.G. was partially supported by the NSF (Grant No. DMS-2054002)

References

Aguilar, K., Chávez, Á., Garcia, S. R., and Volčič, J., Norms on complex matrices induced by complete homogeneous symmetric polynomials . Bull. Lond. Math. Soc. 54(2022), no. 6, 2078–2100.CrossRefGoogle Scholar
Bell, E. T., Exponential polynomials . Ann. Math. 35(1934), no. 2, 258–277.CrossRefGoogle Scholar
Bhatia, R., Matrix analysis, Graduate Texts in Mathematics, 169, Springer,New York, 1997.CrossRefGoogle Scholar
Bhatia, R. and Holbrook, J. A. R., Unitary invariance and spectral variation . Linear Algebra Appl. 95(1987), 43–68.CrossRefGoogle Scholar
Billingsley, P., Probability and measure. 3rd ed., Wiley Series in Probability and Mathematical Statistics, Wiley,New York, 1995.Google Scholar
Birkhoff, G., Three observations on linear algebra . Univ. Nac. Tucumán. Revista A 5(1946), 147–151.Google Scholar
Chávez, Á., Garcia, S. R., and Hurley, J., Norms on complex matrices induced by random vectors . Canad. Math. Bull. 66(2023), no. 3, 808–826.CrossRefGoogle Scholar
Fan, K., On a theorem of Weyl concerning eigenvalues of linear transformations. I . Proc. Natl. Acad. Sci. USA 35(1949), 652–655.CrossRefGoogle ScholarPubMed
Hardy, G. H., Littlewood, J. E., and Pólya, G., Some simple inequalities satisfied by convex functions . Messenger Math. 58(1929), 145–152.Google Scholar
Horn, R. A. and Johnson, C. R., Matrix analysis. 2nd ed., Cambridge University Press,Cambridge, 2013.Google Scholar
Lewis, A. S., Group invariance and convex matrix analysis . SIAM J. Matrix Anal. Appl. 17(1996), no. 4, 927–949.CrossRefGoogle Scholar
Li, C.-K., Inequalities relating norms invariant under unitary similarities . Linear Multilinear Algebra 29(1991), nos. 3–4, 155–167.CrossRefGoogle Scholar
Stanley, R. P., Enumerative combinatorics. Vol. 1, Cambridge Studies in Advanced Mathematics, 49, Cambridge University Press,Cambridge, 1997. With a foreword by Gian-Carlo Rota, Corrected reprint of the 1986 original.CrossRefGoogle Scholar