Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Saxl, Jan
1987.
The complex characters of the symmetric groups that remain irreducible in subgroups.
Journal of Algebra,
Vol. 111,
Issue. 1,
p.
210.
Saradha, N.
and
Shorey, T. N.
1994.
On the equationx(x +d 1)…(x + (k - 1)d 1) =y(y +d 2)…(y + (mk - 1)d 2).
Proceedings Mathematical Sciences,
Vol. 104,
Issue. 1,
p.
1.
Leu, Ming-Guang
1996.
On $L\left( {1,\chi } \right)$ and class number formula for the real quadratic fields.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 72,
Issue. 3,
Zavarnitsin, A. V.
and
Mazurov, V. D.
1999.
Element orders in coverings of symmetric and alternating groups.
Algebra and Logic,
Vol. 38,
Issue. 3,
p.
159.
Zavarnitsine, A. V.
2002.
Recognition by the Set of Element Orders of Symmetric Groups of Degree r and r+1 for Prime r.
Siberian Mathematical Journal,
Vol. 43,
Issue. 5,
p.
808.
Laishram, Shanta
and
Shorey, T.N.
2006.
The greatest prime divisor of a product of terms in an arithmetic progression.
Indagationes Mathematicae,
Vol. 17,
Issue. 3,
p.
425.
Bessenrodt, Christine
2007.
Bar weights of bar partitions and spin character zeros.
Journal of Algebraic Combinatorics,
Vol. 26,
Issue. 1,
p.
107.
Mazurov, V. D.
and
Zavarnitsine, A. V.
2007.
On element orders in coverings of the simple groups L n (q) and U n (q).
Proceedings of the Steklov Institute of Mathematics,
Vol. 257,
Issue. S1,
p.
S145.
Zavarnitsine, A. V.
2008.
Properties of element orders in covers for Ln(q) and Un(q).
Siberian Mathematical Journal,
Vol. 49,
Issue. 2,
p.
246.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
195.
Gorshkov, Ilya B.
2017.
On Thompson’s conjecture for alternating groups of large degree.
Journal of Group Theory,
Vol. 20,
Issue. 4,
p.
719.
Sadler, Garrett
Fang, Fang
Clawson, Richard
and
Irwin, Klee
2019.
Periodic Modification of the Boerdijk–Coxeter Helix (tetrahelix).
Mathematics,
Vol. 7,
Issue. 10,
p.
1001.
Bovdi, Victor
Breuer, Thomas
and
Maróti, Attila
2020.
Finite simple groups with short Galois orbits on conjugacy classes.
Journal of Algebra,
Vol. 544,
Issue. ,
p.
151.
Wu, Hongguang
and
Sheng, JiaLe
2022.
A generalization of a theorem of Sylvester and Schur.
The Ramanujan Journal,
Vol. 58,
Issue. 1,
p.
131.
Jakhar, A.
and
Kalwaniya, R.
2024.
On the second irreducibility theorem of I. Schur.
Acta Mathematica Hungarica,
Vol. 174,
Issue. 2,
p.
289.
Fusari, Marco
Previtali, Andrea
and
Spiga, Pablo
2024.
Cliques in derangement graphs for innately transitive groups.
Journal of Group Theory,
Vol. 27,
Issue. 5,
p.
929.
Pakovich, Fedor
2025.
On iterates of rational functions with maximal number of critical values.
Journal d'Analyse Mathématique,
Vol. 156,
Issue. 1,
p.
213.
Natarajan, Saradha
2025.
Perfect Powers—An Ode to Erdős.
p.
49.
Pejković, Tomislav
2025.
Schneider’s p-adic continued fractions of rational numbers.
The Ramanujan Journal,
Vol. 68,
Issue. 3,
Bannai, Eiichi
Kurihara, Hirotake
and
Nozaki, Hiroshi
2026.
On the existence and non-existence of spherical m-stiff configurations.
Discrete Mathematics,
Vol. 349,
Issue. 1,
p.
114731.

 has a prime divisor ≥p
has a prime divisor ≥p and
and 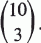 In that paper the author uses some deep results of Rosser and Schoenfeld [5] on the distribution of primes.
In that paper the author uses some deep results of Rosser and Schoenfeld [5] on the distribution of primes.