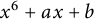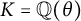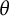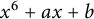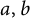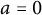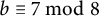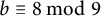Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ben Yakkou, H.
2022.
On monogenity of certain number fields defined by $$x^8+ax+b$$.
Acta Mathematica Hungarica,
Vol. 166,
Issue. 2,
p.
614.
Jakhar, Anuj
Kaur, Sumandeep
and
Kumar, Surender
2022.
Common index divisor of the number fields defined by .
Proceedings of the Edinburgh Mathematical Society,
Vol. 65,
Issue. 4,
p.
1147.
Jakhar, Anuj
and
Kaur, Sumandeep
2023.
A note on non-monogenity of number fields arised from sextic trinomials.
Quaestiones Mathematicae,
Vol. 46,
Issue. 5,
p.
833.
Jakhar, Anuj
Kaur, Sumandeep
and
Kumar, Surender
2023.
On non-monogenity of the number fields defined by certain quadrinomials.
Communications in Algebra,
Vol. 51,
Issue. 6,
p.
2448.
El Fadil, Lhoussain
2023.
On the index divisors and monogenity of number fields defined by
x
5
+
ax
3
+
b
.
Quaestiones Mathematicae,
Vol. 46,
Issue. 11,
p.
2355.
El Fadil, Lhoussain
2023.
On Index and Monogenity of Certain Number Fields Defined by Trinomials.
Mathematica Slovaca,
Vol. 73,
Issue. 4,
p.
861.
Fadil, Lhoussain El
2023.
On common index divisor and monogenity of certain number fields defined by trinomials X6 + AX + B.
Quaestiones Mathematicae,
Vol. 46,
Issue. 8,
p.
1609.
Ben Yakkou, Hamid
2023.
ON NONMONOGENIC NUMBER FIELDS DEFINED BY TRINOMIALS OF TYPE xn+axm+b.
Rocky Mountain Journal of Mathematics,
Vol. 53,
Issue. 3,
Fadil, Lhoussain El
and
Kchit, Omar
2023.
On index divisors and monogenity of certain septic number fields defined by x7 + ax3 + b.
Communications in Algebra,
Vol. 51,
Issue. 6,
p.
2349.
Jakhar, Anuj
2023.
ON NONMONOGENIC ALGEBRAIC NUMBER FIELDS.
Rocky Mountain Journal of Mathematics,
Vol. 53,
Issue. 1,
Boughaleb, Omar
and
Saber, Karim
2024.
On common index divisors and monogenity of certain number fields defined by x^{5}+ax+b.
Boletim da Sociedade Paranaense de Matemática,
Vol. 42,
Issue. ,
p.
1.
Gaál, István
2024.
Monogenity and Power Integral Bases: Recent Developments.
Axioms,
Vol. 13,
Issue. 7,
p.
429.
El Fadil, Lhoussain
and
Gaál, István
2025.
On the Monogenity of Quartic Number Fields Defined by x4 + ax2 + b.
Mathematics,
Vol. 13,
Issue. 6,
p.
905.