Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-22T09:55:17.997Z Has data issue: false hasContentIssue false
  • English
  • Français

On Permanental Identities of Symmetric and Skew-Symmetric Matrices in Characteristic p

Published online by Cambridge University Press:  20 November 2018

Angela Valenti
Angela Valenti*
Affiliation:
Dipartimento di Matematica Università di Palermo Via Archirafi 34 90123 Palermo Italy
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

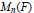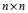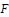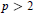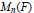Let ${{M}_{n}}(F)$ be the algebra of $n\times n$ matrices over a field $F$ of characteristic $p>2$ and let $*$ be an involution on ${{M}_{n}}(F)$. If 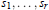${{s}_{1}},...,{{s}_{r}}$ are symmetric variables we determine the smallest $r$ such that the polynomial

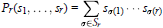$${{P}_{r}}({{S}_{1}},...,{{S}_{r}})\,=\,\sum\limits_{\sigma \in {{S}_{r}}}{{{S}_{\sigma (1)}}...{{S}_{\sigma (r)}}}$$

is a $*$-polynomial identity of 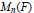${{M}_{n}}(F)$ under either the symplectic or the transpose involution. We also prove an analogous result for the polynomial

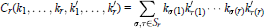$${{C}_{r}}\left( {{k}_{1}},...,{{k}_{r,}}{{{{k}'}}_{1}},...,{{{{k}'}}_{r}} \right)=\sum\limits_{\sigma ,\tau \in {{S}_{r}}}{{{k}_{\sigma \left( 1 \right)}}{{{{k}'}}_{\tau \left( 1 \right)}}\cdot \cdot \cdot {{k}_{\sigma \left( r \right)}}{{{{k}'}}_{\tau \left( r \right)}}}$$

where 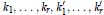${{k}_{1}},...,{{k}_{r}},k_{1}^{'},...,k_{r}^{'}$ are skew variables under the transpose involution.

Keywords

16R50
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 1 , 01 March 1998 , pp. 118 - 124
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Giambruno, A. and Valenti, A., On minimal Ł-identities of matrices. Linear and Multilinear Algebra, 39 (1995), 309–323.Google Scholar
2. Kortesi, P. and Szigeti, J., On permanental identities over matrix rings. Comm. Algebra 22(1994), 159–171.Google Scholar
3. Kostant, B., A theorem of Frobenius, a theorem of Amitsur-Levitzki and cohomology theory. Indiana J. Math. (andMech.) 7 (1958), 237–264.Google Scholar
4. Revesz, G. and Szigeti, J., Identities of symmetric and skew-symmetric matrices in characteristic p. Rend. Circ.Mat. Palermo (2) 44 (1995), 94–106.Google Scholar
5. Rowen, L. H., Standard polynomials in matrix algebras. Trans. Amer.Math. Soc. 190 (1974), 253–284.Google Scholar
6. Rowen, L. H., Polynomial Identities in Ring Theory. Academic Press, New York, 1980.Google Scholar
7. Rowen, L. H., A simple proof of Kostant's theorem, and an analogue for the symplectic involution. Contemp. Math. 13, Amer. Math. Soc., Providence, Rhode Island, 1982, 207–215.Google Scholar
8. Zalesskii, A. E., A symmetric analogue of the Amitsur-Levitzki Theorem. Vests Akad. Navuk BSSR Ser. Fz.-Mat. Navuk (1985), 108–110 (Russian).Google Scholar