No CrossRef data available.
Article contents
On the greatest common divisor of n and the nth Fibonacci number, II
Published online by Cambridge University Press: 06 October 2022
Abstract
Let 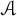 $\mathcal {A}$ be the set of all integers of the form
$\mathcal {A}$ be the set of all integers of the form 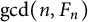 $\gcd (n, F_n)$, where n is a positive integer and
$\gcd (n, F_n)$, where n is a positive integer and 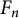 $F_n$ denotes the nth Fibonacci number. Leonetti and Sanna proved that
$F_n$ denotes the nth Fibonacci number. Leonetti and Sanna proved that 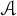 $\mathcal {A}$ has natural density equal to zero, and asked for a more precise upper bound. We prove that for all sufficiently large x. In fact, we prove that a similar bound also holds when the sequence of Fibonacci numbers is replaced by a general nondegenerate Lucas sequence.
$\mathcal {A}$ has natural density equal to zero, and asked for a more precise upper bound. We prove that for all sufficiently large x. In fact, we prove that a similar bound also holds when the sequence of Fibonacci numbers is replaced by a general nondegenerate Lucas sequence.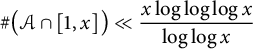 $$ \begin{align*} \#\big(\mathcal{A} \cap [1, x]\big) \ll \frac{x \log \log \log x}{\log \log x} \end{align*} $$
$$ \begin{align*} \#\big(\mathcal{A} \cap [1, x]\big) \ll \frac{x \log \log \log x}{\log \log x} \end{align*} $$
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
References
Ailon, N. and Rudnick, Z.,
Torsion points on curves and common divisors of
 ${a}^k-1$
and
${a}^k-1$
and
 ${b}^k-1$
. Acta Arith. 113(2004), no. 1, 31–38.CrossRefGoogle Scholar
${b}^k-1$
. Acta Arith. 113(2004), no. 1, 31–38.CrossRefGoogle Scholar
Alba González, J. J., Luca, F., Pomerance, C., and Shparlinski, I. E.,
On numbers
 $n$
dividing the
$n$
dividing the
 $n$
th term of a linear recurrence
. Proc. Edinb. Math. Soc. (2) 55(2012), no. 2, 271–289.CrossRefGoogle Scholar
$n$
th term of a linear recurrence
. Proc. Edinb. Math. Soc. (2) 55(2012), no. 2, 271–289.CrossRefGoogle Scholar
André-Jeannin, R.,
Divisibility of generalized Fibonacci and Lucas numbers by their subscripts
. Fibonacci Quart. 29(1991), no. 4, 364–366.Google Scholar
Bilu, Y., Hanrot, G., and Voutier, P. M.,
Existence of primitive divisors of Lucas and Lehmer numbers
. J. Reine Angew. Math. 539(2001), 75–122, with an appendix by M. Mignotte.Google Scholar
Bugeaud, Y., Corvaja, P., and Zannier, U., An upper bound for the G.C.D. of
 ${a}^n-1$
and
${a}^n-1$
and
 ${b}^n-1$
. Math. Z. 243(2003), no. 1, 79–84.CrossRefGoogle Scholar
${b}^n-1$
. Math. Z. 243(2003), no. 1, 79–84.CrossRefGoogle Scholar
Cubre, P. and Rouse, J.,
Divisibility properties of the Fibonacci entry point
. Proc. Amer. Math. Soc. 142(2014), no. 11, 3771–3785.CrossRefGoogle Scholar
Halberstam, H. and Richert, H.-E., Sieve methods, London Mathematical Society Monographs, 4, Academic Press [Harcourt Brace Jovanovich], London–New York, 1974.Google Scholar
Jha, A.,
On terms in a dynamical divisibility sequence having a fixed G.C.D. with their indices
. New York J. Math. 28(2022), 1152–1171.Google Scholar
Jha, A. and Nath, A., The distribution of G.C.D.s of shifted primes and Lucas sequences. Preprint, 2022. arXiv:2207.00825Google Scholar
Jha, A. and Sanna, C.,
Greatest common divisors of shifted primes and Fibonacci numbers
. Res. Number Theory 8(2022), no. 4, Article no. 65.CrossRefGoogle Scholar
Kim, S.,
The density of the terms in an elliptic divisibility sequence having a fixed G.C.D. with their indices
. J. Number Theory 207(2020), 22–41, with an appendix by M. Ram Murty.CrossRefGoogle Scholar
Leonetti, P. and Sanna, C.,
On the greatest common divisor of
 $n$
and the
$n$
and the
 $n$
th Fibonacci number
. Rocky Mountain J. Math. 48(2018), no. 4, 1191–1199.CrossRefGoogle Scholar
$n$
th Fibonacci number
. Rocky Mountain J. Math. 48(2018), no. 4, 1191–1199.CrossRefGoogle Scholar
Luca, F. and Tron, E.,
The distribution of self-Fibonacci divisors
. In: Advances in the theory of numbers, Fields Institute Communication, 77, Fields Institute for Research in Mathematical Sciences, Toronto, ON, 2015, pp. 149–158.CrossRefGoogle Scholar
Mastrostefano, D.,
An upper bound for the moments of a GCD related to Lucas sequences
. Rocky Mountain J. Math. 49(2019), no. 3, 887–902.CrossRefGoogle Scholar
Mastrostefano, D. and Sanna, C.,
On numbers
 $n$
with polynomial image coprime with the
$n$
with polynomial image coprime with the
 $n$
th term of a linear recurrence
. Bull. Aust. Math. Soc. 99(2019), no. 1, 23–33.CrossRefGoogle Scholar
$n$
th term of a linear recurrence
. Bull. Aust. Math. Soc. 99(2019), no. 1, 23–33.CrossRefGoogle Scholar
Moree, P.,
On primes
 $p$
for which
$p$
for which
 $d$
divides
$d$
divides
 ${ord}_p(g)$
. Funct. Approx. Comment. Math. 33(2005), 85–95.CrossRefGoogle Scholar
${ord}_p(g)$
. Funct. Approx. Comment. Math. 33(2005), 85–95.CrossRefGoogle Scholar
OEIS Foundation Inc., The On-Line Encyclopedia of Integer Sequences, 2022, published electronically at https://oeis.org
Google Scholar
Pollack, P.,
Numbers which are orders only of cyclic groups
. Proc. Amer. Math. Soc. 150(2022), no. 2, 515–524.CrossRefGoogle Scholar
Pomerance, C.,
On the distribution of amicable numbers
. J. Reine Angew. Math. 293(1977), no. 294, 217–222.Google Scholar
Renault, M.,
The period, rank, and order of the
 $\left(a,b\right)$
– Fibonacci sequence
$\left(a,b\right)$
– Fibonacci sequence
 $\mathit{\mathsf{\operatorname{mod}}}\;m$
. Math. Mag. 86(2013), no. 5, 372–380.CrossRefGoogle Scholar
$\mathit{\mathsf{\operatorname{mod}}}\;m$
. Math. Mag. 86(2013), no. 5, 372–380.CrossRefGoogle Scholar
Ribenboim, P., My numbers, my friends: popular lectures on number theory, Springer, New York, 2000.CrossRefGoogle Scholar
Sanna, C.,
On numbers
 $n$
dividing the
$n$
dividing the
 $n$
th term of a Lucas sequence
. Int. J. Number Theory 13(2017), no. 3, 725–734.CrossRefGoogle Scholar
$n$
th term of a Lucas sequence
. Int. J. Number Theory 13(2017), no. 3, 725–734.CrossRefGoogle Scholar
Sanna, C.,
The moments of the logarithm of a G.C.D. related to Lucas sequences
. J. Number Theory 191(2018), 305–315.CrossRefGoogle Scholar
Sanna, C.,
On numbers
 $n$
relatively prime to the
$n$
relatively prime to the
 $n$
th term of a linear recurrence
. Bull. Malays. Math. Sci. Soc. 42(2019), no. 2, 827–833.CrossRefGoogle Scholar
$n$
th term of a linear recurrence
. Bull. Malays. Math. Sci. Soc. 42(2019), no. 2, 827–833.CrossRefGoogle Scholar
Sanna, C.,
On the divisibility of the rank of appearance of a Lucas sequence
. Int. J. Number Theory 18(2022), no. 10, 2145–2156.CrossRefGoogle Scholar
Sanna, C. and Tron, E.,
The density of numbers
 $n$
having a prescribed G.C.D. with the
$n$
having a prescribed G.C.D. with the
 $n$
th Fibonacci number
. Indag. Math. (N.S.) 29(2018), no. 3, 972–980.CrossRefGoogle Scholar
$n$
th Fibonacci number
. Indag. Math. (N.S.) 29(2018), no. 3, 972–980.CrossRefGoogle Scholar
Silverman, J. H.,
Generalized greatest common divisors, divisibility sequences, and Vojta’s conjecture for blowups
. Monatsh. Math. 145(2005), no. 4, 333–350.CrossRefGoogle Scholar
Somer, L.,
Divisibility of terms in Lucas sequences by their subscripts
. In: Applications of Fibonacci numbers (St. Andrews, 1992). Vol. 5, Kluwer Academic Publishers, Dordrecht, 1993, pp. 515–525.CrossRefGoogle Scholar
Tenenbaum, G., Introduction to analytic and probabilistic number theory, 3rd ed., Graduate Studies in Mathematics, 163, American Mathematical Society, Providence, RI, 2015, translated from the 2008 French edition by Patrick D. F. Ion.CrossRefGoogle Scholar
Tron, E.,
The greatest common divisor of linear recurrences
. Rend. Semin. Mat. Univ. Politec. Torino 78(2020), no. 1, 103–124.Google Scholar


