Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Abu-Khuzam, Hazar
and
Bell, Howard E.
2003.
On Rings With Conditions On Nonperiodic Elements.
Results in Mathematics,
Vol. 43,
Issue. 3-4,
p.
198.


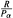 contains no nontrivial periodic ideals. We also prove that
contains no nontrivial periodic ideals. We also prove that 