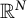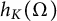1 Introduction
Given an open, bounded set
![]() $\Omega $
in
$\Omega $
in
![]() $\mathbb {R}^N$
, the Cheeger problem amounts to finding sets attaining the Cheeger constant
$\mathbb {R}^N$
, the Cheeger problem amounts to finding sets attaining the Cheeger constant
![]() $h(\Omega )$
, which is defined as
$h(\Omega )$
, which is defined as
 $$ \begin{align} h(\Omega) := \inf \left\{\,\frac{\operatorname{\mathrm{Per}}(E)}{|E|}\,:\, E\subset \Omega, \, |E|>0 \,\right\}, \end{align} $$
$$ \begin{align} h(\Omega) := \inf \left\{\,\frac{\operatorname{\mathrm{Per}}(E)}{|E|}\,:\, E\subset \Omega, \, |E|>0 \,\right\}, \end{align} $$
where
![]() $\operatorname {\mathrm {Per}}(E)$
denotes the variational perimeter of E, and
$\operatorname {\mathrm {Per}}(E)$
denotes the variational perimeter of E, and
![]() $|E|$
its N-dimensional Lebesgue measure. This problem has been first introduced in the Riemannian setting in [Reference Cheeger5], and it has been deeply studied ever since, given its many applications in different problems. We refer the interested reader to the two surveys [Reference Leonardi12, Reference Parini22]. The computation of the constant and the geometric characterization of minimizers is by now well understood in the two-dimensional case for convex sets [Reference Kawohl and Lachand-Robert10], strips [Reference Leonardi and Pratelli14], and more general sets [Reference Leonardi, Neumayer and Saracco13, Reference Leonardi and Saracco15].
$|E|$
its N-dimensional Lebesgue measure. This problem has been first introduced in the Riemannian setting in [Reference Cheeger5], and it has been deeply studied ever since, given its many applications in different problems. We refer the interested reader to the two surveys [Reference Leonardi12, Reference Parini22]. The computation of the constant and the geometric characterization of minimizers is by now well understood in the two-dimensional case for convex sets [Reference Kawohl and Lachand-Robert10], strips [Reference Leonardi and Pratelli14], and more general sets [Reference Leonardi, Neumayer and Saracco13, Reference Leonardi and Saracco15].
A generalization of this problem can be given in the anisotropic Euclidean space, that is, the Euclidean space endowed with a norm induced by a convex, central-symmetric set. In turns, this underlying anisotropic metric induces a notion of anisotropic perimeter, that can be used to define an anisotropic analogous of (1.1).
More precisely, let
![]() $\mathcal {K}_N$
be the class of (nonempty) open, bounded and centrally symmetric (with respect to the origin) convex sets in
$\mathcal {K}_N$
be the class of (nonempty) open, bounded and centrally symmetric (with respect to the origin) convex sets in
![]() $\mathbb {R}^N$
. Given any
$\mathbb {R}^N$
. Given any
![]() $K\in \mathcal {K}_N$
, its polar set
$K\in \mathcal {K}_N$
, its polar set
![]() $K^\circ $
is defined as
$K^\circ $
is defined as
For every
![]() $K \in \mathcal {K}_N$
, its polar set
$K \in \mathcal {K}_N$
, its polar set
![]() $K^\circ $
belongs to
$K^\circ $
belongs to
![]() $\mathcal {K}_N$
, and
$\mathcal {K}_N$
, and
![]() $(K^\circ )^\circ = K$
(we refer to [Reference Schneider27] for these standard facts). In particular, given any such K, the map
$(K^\circ )^\circ = K$
(we refer to [Reference Schneider27] for these standard facts). In particular, given any such K, the map
![]() $\Phi _K^\circ $
defined as
$\Phi _K^\circ $
defined as
is a norm over
![]() $\mathbb {R}^N$
, called polar norm of K. By definition,
$\mathbb {R}^N$
, called polar norm of K. By definition,
that is,
![]() $K^\circ $
is the unit ball with respect to the metric induced by
$K^\circ $
is the unit ball with respect to the metric induced by
![]() $\Phi ^\circ $
.
$\Phi ^\circ $
.
By means of the polar norm, it is possible to define an anisotropic perimeter for any Borel set E as
where
![]() $\partial ^*E$
denotes the reduced boundary of E (see [Reference Maggi16]).
$\partial ^*E$
denotes the reduced boundary of E (see [Reference Maggi16]).
Notice that such a perimeter is invariant under translation but, in general, not under the effect of the rotation group
![]() $\mathrm {SO}(N)$
. The anisotropic isoperimetric inequality [Reference Taylor29] states that, among sets E of fixed volume, the unique anisotropic perimeter minimizer (up to translations) is given by a dilation of the convex set K, which is called Wulff shape associated with
$\mathrm {SO}(N)$
. The anisotropic isoperimetric inequality [Reference Taylor29] states that, among sets E of fixed volume, the unique anisotropic perimeter minimizer (up to translations) is given by a dilation of the convex set K, which is called Wulff shape associated with
![]() $\Phi ^\circ $
, i.e.,
$\Phi ^\circ $
, i.e.,
where
![]() $K_E$
is the dilation of K such that
$K_E$
is the dilation of K such that
![]() $|E|=|K_E|$
.
$|E|=|K_E|$
.
With this notion of anisotropic perimeter (1.3) at our disposal, we can define the K-Cheeger constant of a set
![]() $\Omega $
analogously to (1.1) as
$\Omega $
analogously to (1.1) as
 $$ \begin{align} h_K(\Omega) := \inf \left \{ \frac{\operatorname{\mathrm{Per}}_K(E)}{|E|} \colon E\subset \Omega\,, |E|>0 \right\}. \end{align} $$
$$ \begin{align} h_K(\Omega) := \inf \left \{ \frac{\operatorname{\mathrm{Per}}_K(E)}{|E|} \colon E\subset \Omega\,, |E|>0 \right\}. \end{align} $$
Sets attaining the infimum are called K-Cheeger sets of
![]() $\Omega $
, and it is well known that they exist for any
$\Omega $
, and it is well known that they exist for any
![]() $\Omega $
regular enough with finite measure [Reference Kawohl and Novaga11, Reference Saracco26]. The constant
$\Omega $
regular enough with finite measure [Reference Kawohl and Novaga11, Reference Saracco26]. The constant
![]() $h_K(\Omega )$
, whenever
$h_K(\Omega )$
, whenever
![]() $\Omega $
is Lipschitz regular, can be thought of as the first eigenvalue of the anisotropic
$\Omega $
is Lipschitz regular, can be thought of as the first eigenvalue of the anisotropic
![]() $1$
-Laplacian [Reference Kawohl and Novaga11]; it is related to anisotropic capillarity problems [Reference Amato, Bellettini and Tealdi1], and it is relevant for applications to image reconstruction [Reference Caselles, Facciolo and Meinhardt4].
$1$
-Laplacian [Reference Kawohl and Novaga11]; it is related to anisotropic capillarity problems [Reference Amato, Bellettini and Tealdi1], and it is relevant for applications to image reconstruction [Reference Caselles, Facciolo and Meinhardt4].
A usual problem for shape functionals is to determine which shapes
![]() $\Omega $
minimize the functional
$\Omega $
minimize the functional
![]() $\Omega \mapsto h_K(\Omega )$
under a volume constraint on
$\Omega \mapsto h_K(\Omega )$
under a volume constraint on
![]() $\Omega $
. The anisotropic isoperimetric inequality (1.4) immediately implies that the minimizing shape is a dilation of K itself, and, in particular, we have
$\Omega $
. The anisotropic isoperimetric inequality (1.4) immediately implies that the minimizing shape is a dilation of K itself, and, in particular, we have
While in (1.6) the set
![]() $K\in \mathcal {K}_N$
providing the metric is fixed and one minimizes among
$K\in \mathcal {K}_N$
providing the metric is fixed and one minimizes among
![]() $\Omega $
, in the present paper, we fix
$\Omega $
, in the present paper, we fix
![]() $\Omega $
and want to minimize among the metrics K—under suitable constraints.
$\Omega $
and want to minimize among the metrics K—under suitable constraints.
There are two possible reasonable choices for the volume constraint: either on the volume of the Wulff shape
![]() $|K|$
, or on the volume of the unit ball
$|K|$
, or on the volume of the unit ball
![]() $|K^\circ |$
, leading to the study of the two (scaling invariant) functionals
$|K^\circ |$
, leading to the study of the two (scaling invariant) functionals
Since we are interested in the metric, it feels more natural to impose a constraint on the volume of the unit ball
![]() $K^\circ $
, that is, to consider (1.8). It is noteworthy that not only it is the more natural choice, but also the minimization of (1.7) is a trivial task, whenever
$K^\circ $
, that is, to consider (1.8). It is noteworthy that not only it is the more natural choice, but also the minimization of (1.7) is a trivial task, whenever
![]() $\Omega $
is fixed in
$\Omega $
is fixed in
![]() $\mathcal {K}_N$
. Indeed, by the anisotropic isoperimetric inequality (1.4), for every
$\mathcal {K}_N$
. Indeed, by the anisotropic isoperimetric inequality (1.4), for every
![]() $E \subset \Omega $
, one has
$E \subset \Omega $
, one has
with equality holding if and only if E equals
![]() $K_E$
up to a translation. Therefore,
$K_E$
up to a translation. Therefore,
Passing to the infimum on all
![]() $E \subset \Omega $
, we obtain
$E \subset \Omega $
, we obtain
for all possible
![]() $K\in \mathcal {K}_N$
. In particular, equality holds if and only if K coincides with
$K\in \mathcal {K}_N$
. In particular, equality holds if and only if K coincides with
![]() $\Omega $
(up to translations and dilations), and
$\Omega $
(up to translations and dilations), and
![]() $\Omega $
is the associated Cheeger set. Summing up, if
$\Omega $
is the associated Cheeger set. Summing up, if
![]() $\Omega \in \mathcal {K}_N$
, one has
$\Omega \in \mathcal {K}_N$
, one has
and
![]() $K=\Omega $
is the unique minimizer.
$K=\Omega $
is the unique minimizer.
On the other hand, the minimization of (1.8) is far from being trivial. Notice that we can immediately rewrite
![]() $\mathcal {J}_\Omega $
as
$\mathcal {J}_\Omega $
as
We have already observed that the first factor of the above product is minimized in
![]() $\mathcal {K}_N$
by the choice
$\mathcal {K}_N$
by the choice
![]() $K=\Omega $
, provided that
$K=\Omega $
, provided that
![]() $\Omega \in \mathcal {K}_N$
. The second factor is known as the Mahler volume of K, a shape functional which is invariant under invertible affine transformations, and which is well known to be maximized by balls (in general, ellipsoids [Reference Santaló25]). Regarding its minimization, it is conjectured to be minimized by (affine transformations of) hypercubes (in general, Hanner’s polytopes). This holds true in dimension
$\Omega \in \mathcal {K}_N$
. The second factor is known as the Mahler volume of K, a shape functional which is invariant under invertible affine transformations, and which is well known to be maximized by balls (in general, ellipsoids [Reference Santaló25]). Regarding its minimization, it is conjectured to be minimized by (affine transformations of) hypercubes (in general, Hanner’s polytopes). This holds true in dimension
![]() $N=2$
(see [Reference Mahler17]) and under some additional assumptions in higher dimension (see [Reference Reisner24]). We refer to the expository article [Reference Tao28, Chapter 3.3] for further details. Therefore, when
$N=2$
(see [Reference Mahler17]) and under some additional assumptions in higher dimension (see [Reference Reisner24]). We refer to the expository article [Reference Tao28, Chapter 3.3] for further details. Therefore, when
![]() $N=2$
and
$N=2$
and
![]() $\Omega $
is a parallelogram, the minimization is trivial, while otherwise a competition between the two terms arises.
$\Omega $
is a parallelogram, the minimization is trivial, while otherwise a competition between the two terms arises.
Similar problems of finding the best metric have been studied, for instance, for the eigenvalues of the Laplace–Beltrami operator on the sphere
![]() $\mathbb {S}^2$
(see [Reference Hersch8, Reference Karpukhin, Nadirashvili, Penskoi and Polterovich9, Reference Nadirashvili19, Reference Nadirashvili and Sire20]). In the same spirit, one could consider minimization problems with respect to the underlying metric for different shape functionals, e.g., depending on the eigenvalues of the anisotropic p-Laplacian, the K-capacity, or K-torsion. We leave these problems as further research directions, as they have an intrinsic higher difficulty due to the fact that they involve nongeometrical quantities.
$\mathbb {S}^2$
(see [Reference Hersch8, Reference Karpukhin, Nadirashvili, Penskoi and Polterovich9, Reference Nadirashvili19, Reference Nadirashvili and Sire20]). In the same spirit, one could consider minimization problems with respect to the underlying metric for different shape functionals, e.g., depending on the eigenvalues of the anisotropic p-Laplacian, the K-capacity, or K-torsion. We leave these problems as further research directions, as they have an intrinsic higher difficulty due to the fact that they involve nongeometrical quantities.
In the present paper, we focus on the planar case. Moreover, we will always suppose that the set
![]() $\Omega \subset \mathbb {R}^2$
is convex, since in this case we can exploit the structure of K-Cheeger sets granted by [Reference Kawohl and Novaga11, Theorem 5.1]. In Section 3, we prove that there exist minimizers of
$\Omega \subset \mathbb {R}^2$
is convex, since in this case we can exploit the structure of K-Cheeger sets granted by [Reference Kawohl and Novaga11, Theorem 5.1]. In Section 3, we prove that there exist minimizers of
![]() $\mathcal {J}_\Omega $
, while its supremum is
$\mathcal {J}_\Omega $
, while its supremum is
![]() $+\infty $
. In Section 4, we show by means of an example that the problem is indeed nontrivial: in the case
$+\infty $
. In Section 4, we show by means of an example that the problem is indeed nontrivial: in the case
![]() $\Omega =B$
, we prove that the square is the shape that yields the lowest energy among all regular n-gons, and we conjecture it to be the best shape among all possible centrally symmetric anisotropies.
$\Omega =B$
, we prove that the square is the shape that yields the lowest energy among all regular n-gons, and we conjecture it to be the best shape among all possible centrally symmetric anisotropies.
2 Preliminary results
2.1 The anisotropic Cheeger problem
Let
![]() $K \in \mathcal {K}_N$
, and let
$K \in \mathcal {K}_N$
, and let
![]() $\Omega \subset \mathbb {R}^N$
be an open, bounded (nonempty) set. A K-Cheeger set is a non-negligible measurable set
$\Omega \subset \mathbb {R}^N$
be an open, bounded (nonempty) set. A K-Cheeger set is a non-negligible measurable set
![]() $C_K \subset \Omega $
such that
$C_K \subset \Omega $
such that
Whenever
![]() $\Omega $
is a convex, two-dimensional set, there exists a unique K-Cheeger set
$\Omega $
is a convex, two-dimensional set, there exists a unique K-Cheeger set
![]() $C_K \subset \Omega $
. Moreover, it is possible to give a complete geometrical characterization of
$C_K \subset \Omega $
. Moreover, it is possible to give a complete geometrical characterization of
![]() $C_K$
, which we recall in Theorem 2.1. This has been first proved in the isotropic Euclidean setting [Reference Kawohl and Lachand-Robert10] and later extended to the anisotropic Euclidean setting in [Reference Kawohl and Novaga11]. For the ease of the reader, before stating the result, we recall the definition of Minkowski addition and difference between two sets E and F. Given any
$C_K$
, which we recall in Theorem 2.1. This has been first proved in the isotropic Euclidean setting [Reference Kawohl and Lachand-Robert10] and later extended to the anisotropic Euclidean setting in [Reference Kawohl and Novaga11]. For the ease of the reader, before stating the result, we recall the definition of Minkowski addition and difference between two sets E and F. Given any
![]() $x\in \mathbb {R}^2$
, if we denote by
$x\in \mathbb {R}^2$
, if we denote by
![]() $E+x$
, the translation of the set E by x, we have
$E+x$
, the translation of the set E by x, we have
 $$ \begin{align*} E\oplus F &:= \cup_{x\in F} (E+x),\\ E\ominus F &:= \cap_{x\in F} (E-x). \end{align*} $$
$$ \begin{align*} E\oplus F &:= \cup_{x\in F} (E+x),\\ E\ominus F &:= \cap_{x\in F} (E-x). \end{align*} $$
When F is chosen as a ball B, the Minkowski addition
![]() $E\oplus B$
can be thought as an outward regularization of the set E, and the Minkowski difference
$E\oplus B$
can be thought as an outward regularization of the set E, and the Minkowski difference
![]() $E\ominus B$
as an inward regularization. We remark that, in general, these operations do not commute and one only has the set inclusion
$E\ominus B$
as an inward regularization. We remark that, in general, these operations do not commute and one only has the set inclusion
![]() $(E\ominus B) \oplus B \subset E$
.
$(E\ominus B) \oplus B \subset E$
.
Theorem 2.1 [Reference Kawohl and Novaga11, Theorem 5.1]
Let
![]() $\Omega \subset \mathbb {R}^2$
be an open, bounded, convex set. Then, there exists a unique K-Cheeger set
$\Omega \subset \mathbb {R}^2$
be an open, bounded, convex set. Then, there exists a unique K-Cheeger set
![]() $C_K$
of
$C_K$
of
![]() $\Omega $
. Moreover,
$\Omega $
. Moreover,
![]() $C_K$
is convex and we have
$C_K$
is convex and we have
where
![]() $\Omega ^\rho := \Omega \ominus \rho K$
and
$\Omega ^\rho := \Omega \ominus \rho K$
and
![]() $\rho $
is the inverse of the K-Cheeger constant. Moreover,
$\rho $
is the inverse of the K-Cheeger constant. Moreover,
![]() $\rho $
is the unique value such that
$\rho $
is the unique value such that
![]() $|\Omega ^{\rho }|=\rho ^2 |K|$
.
$|\Omega ^{\rho }|=\rho ^2 |K|$
.
2.2 The Mahler volume
Let
![]() $K \subset \mathbb {R}^N$
be a convex set. The Mahler volume of K is the quantity
$K \subset \mathbb {R}^N$
be a convex set. The Mahler volume of K is the quantity
where
![]() $K^\circ $
is the polar set of K. It can be proven that the Mahler volume is invariant under invertible affine transformations. The following result holds true.
$K^\circ $
is the polar set of K. It can be proven that the Mahler volume is invariant under invertible affine transformations. The following result holds true.
Proposition 2.2 Let K be any convex set in
![]() $\mathcal {K}_2$
, and let
$\mathcal {K}_2$
, and let
![]() $V(K)$
be its Mahler volume. Then
$V(K)$
be its Mahler volume. Then
where Q is a square and B is a ball.
The upper bound is known as Blaschke–Santaló inequality, whose proof can be found in [Reference Schneider27, Section 10.5]. The lower bound was proven in [Reference Mahler17], and an accessible proof can be found in [Reference Thompson30].
2.3 Uniform convergence of polar norms
The following result provides a link between convergence of the metrics in the Hausdorff distance of convex sets, and local uniform convergence of the associated polar norms.
Proposition 2.3 Let
![]() $K \in \mathcal {K}_N$
and
$K \in \mathcal {K}_N$
and
![]() $\{K_n\}_{n\in \mathbb {N}} \subset \mathcal {K}_N$
be a sequence such that
$\{K_n\}_{n\in \mathbb {N}} \subset \mathcal {K}_N$
be a sequence such that
![]() $K_n \to K$
in the Hausdorff topology. Then,
$K_n \to K$
in the Hausdorff topology. Then,
![]() $\Phi _{K_n}^\circ \to \Phi _{K}^\circ $
locally uniformly.
$\Phi _{K_n}^\circ \to \Phi _{K}^\circ $
locally uniformly.
Proof Let
![]() $\varepsilon> 0$
, for n sufficiently big,
$\varepsilon> 0$
, for n sufficiently big,
![]() $(1-\varepsilon )K \subset K_n \subset (1+\varepsilon )K$
. If
$(1-\varepsilon )K \subset K_n \subset (1+\varepsilon )K$
. If
![]() $y \in \mathbb {S}^{N-1}$
, it holds
$y \in \mathbb {S}^{N-1}$
, it holds
which implies
By the
![]() $1$
-homogeneity of
$1$
-homogeneity of
![]() $\Phi _{K}^\circ $
and
$\Phi _{K}^\circ $
and
![]() $\Phi _{K_n}^\circ $
, we obtain the claim.
$\Phi _{K_n}^\circ $
, we obtain the claim.
3 Main results
Throughout this section, we will restrict to the two-dimensional case, and we will suppose that
![]() $\Omega $
is an open, bounded, convex planar set. We consider the functional
$\Omega $
is an open, bounded, convex planar set. We consider the functional
![]() $\mathcal {J}_\Omega $
introduced in (1.8), that is,
$\mathcal {J}_\Omega $
introduced in (1.8), that is,
where the multiplicative factor
![]() $|K^\circ |^{\frac 12}$
appears in order to make it scale invariant.
$|K^\circ |^{\frac 12}$
appears in order to make it scale invariant.
Proposition 3.1 Let
![]() $\Omega \subset \mathbb {R}^2$
be an open, bounded, convex set. Let
$\Omega \subset \mathbb {R}^2$
be an open, bounded, convex set. Let
![]() $V>0$
, and let
$V>0$
, and let
![]() $\{K_n\}_{n \in \mathbb {N}} \subset \mathcal {K}_2$
be a sequence such that
$\{K_n\}_{n \in \mathbb {N}} \subset \mathcal {K}_2$
be a sequence such that
![]() $|K_n|=V$
for every
$|K_n|=V$
for every
![]() $n \in \mathbb {N}$
, with
$n \in \mathbb {N}$
, with
![]() $\operatorname {\mathrm {diam}}(K_n) \to +\infty $
. Then,
$\operatorname {\mathrm {diam}}(K_n) \to +\infty $
. Then,
Proof By Theorem 2.1, the Cheeger set
![]() $C_{K_n}$
of
$C_{K_n}$
of
![]() $\Omega $
associated with the anisotropy
$\Omega $
associated with the anisotropy
![]() $K_n$
is given by
$K_n$
is given by
where the union is taken among all dilations of the Wulff shape
![]() $K_n$
by
$K_n$
by
![]() $\rho _n$
that are contained in
$\rho _n$
that are contained in
![]() $\Omega $
. Since
$\Omega $
. Since
![]() $\operatorname {\mathrm {diam}}(K_n) \to +\infty $
as
$\operatorname {\mathrm {diam}}(K_n) \to +\infty $
as
![]() $n \to +\infty $
, it must necessarily hold
$n \to +\infty $
, it must necessarily hold
![]() $\rho _n \to 0$
. Recalling that
$\rho _n \to 0$
. Recalling that
![]() $h_{K_n}(\Omega )=\rho _n^{-1}$
, one infers that
$h_{K_n}(\Omega )=\rho _n^{-1}$
, one infers that
![]() $h_{K_n}(\Omega ) \to +\infty $
as
$h_{K_n}(\Omega ) \to +\infty $
as
![]() $n \to +\infty $
. By the reverse Mahler inequality contained in Proposition 2.2, the quantities
$n \to +\infty $
. By the reverse Mahler inequality contained in Proposition 2.2, the quantities
![]() $|K_n^\circ |$
are uniformly bounded from below. Therefore,
$|K_n^\circ |$
are uniformly bounded from below. Therefore,
![]() $\lim _{n \to +\infty } \mathcal {J}_\Omega [K_n] = +\infty $
.
$\lim _{n \to +\infty } \mathcal {J}_\Omega [K_n] = +\infty $
.
Corollary 3.2 Let
![]() $\Omega \subset \mathbb {R}^2$
be an open, bounded, convex set. Then,
$\Omega \subset \mathbb {R}^2$
be an open, bounded, convex set. Then,
We now prove that our shape functional
![]() $K\mapsto \mathcal {J}_\Omega [K]$
has a minimizer.
$K\mapsto \mathcal {J}_\Omega [K]$
has a minimizer.
Proposition 3.3 There exists
![]() $\hat {K} \in \mathcal {K}_2$
such that
$\hat {K} \in \mathcal {K}_2$
such that
Proof Let
![]() $\{K_n\}_{n \in \mathbb {N}}$
be a minimizing sequence. Without loss of generality, we can suppose that
$\{K_n\}_{n \in \mathbb {N}}$
be a minimizing sequence. Without loss of generality, we can suppose that
![]() $|K_n|=V$
for some
$|K_n|=V$
for some
![]() $V>0$
. By Mahler’s inequality, the volumes of the polar sets
$V>0$
. By Mahler’s inequality, the volumes of the polar sets
![]() $K_n^\circ $
are uniformly bounded from above. If
$K_n^\circ $
are uniformly bounded from above. If
![]() $\operatorname {\mathrm {diam}}(K_n) \to +\infty $
as
$\operatorname {\mathrm {diam}}(K_n) \to +\infty $
as
![]() $n \to +\infty $
, by Proposition 3.1, it would hold
$n \to +\infty $
, by Proposition 3.1, it would hold
![]() $\mathcal {J}_\Omega [K_n] \to +\infty $
, a contradiction. Therefore,
$\mathcal {J}_\Omega [K_n] \to +\infty $
, a contradiction. Therefore,
![]() $\operatorname {\mathrm {diam}}(K_n)$
is uniformly bounded. By Blaschke’s Selection Theorem [Reference Schneider27, Theorem 1.8.7], there exists
$\operatorname {\mathrm {diam}}(K_n)$
is uniformly bounded. By Blaschke’s Selection Theorem [Reference Schneider27, Theorem 1.8.7], there exists
![]() $\hat {K} \in \mathcal {K}_2$
such that
$\hat {K} \in \mathcal {K}_2$
such that
![]() $K_n \to \hat {K}$
in the Hausdorff topology. By Proposition 2.3,
$K_n \to \hat {K}$
in the Hausdorff topology. By Proposition 2.3,
from which we also infer the
![]() $L^1_{\text {loc}}$
convergence of
$L^1_{\text {loc}}$
convergence of
![]() $K^\circ _n \to \hat {K}^\circ $
, and thus
$K^\circ _n \to \hat {K}^\circ $
, and thus
![]() $|\hat {K}^\circ |\le \liminf _n |K_n^\circ |$
. Let
$|\hat {K}^\circ |\le \liminf _n |K_n^\circ |$
. Let
![]() $C_{K_n}$
be the Cheeger sets associated with
$C_{K_n}$
be the Cheeger sets associated with
![]() $h_{K_n}(\Omega )$
. By Theorem 2.1, all these sets are convex, and they are contained in the bounded set
$h_{K_n}(\Omega )$
. By Theorem 2.1, all these sets are convex, and they are contained in the bounded set
![]() $\Omega $
. Again by Blaschke’s Selection Theorem, up to a subsequence which we do not relabel, there exists a set
$\Omega $
. Again by Blaschke’s Selection Theorem, up to a subsequence which we do not relabel, there exists a set
![]() $\hat {C} \subset \Omega $
that is the Hausdorff limit of the sequence. In particular,
$\hat {C} \subset \Omega $
that is the Hausdorff limit of the sequence. In particular,
![]() $C_{K_n}$
converge to
$C_{K_n}$
converge to
![]() $\hat {C}$
in the sense of characteristic functions. By [Reference Neumayer21, Proposition 2.1] and the local uniform convergence of
$\hat {C}$
in the sense of characteristic functions. By [Reference Neumayer21, Proposition 2.1] and the local uniform convergence of
![]() $\Phi _{K_n}^\circ $
to
$\Phi _{K_n}^\circ $
to
![]() $\Phi ^\circ _K$
, it holds
$\Phi ^\circ _K$
, it holds
Moreover,
![]() $|C_{K_n}|\to |\hat {C}|$
and
$|C_{K_n}|\to |\hat {C}|$
and
![]() $|\hat {C}|>0$
as otherwise, also taking into account that
$|\hat {C}|>0$
as otherwise, also taking into account that
![]() $|K^\circ _n|$
is uniformly bounded from above, the anisotropic isoperimetric inequality would contradict the fact that
$|K^\circ _n|$
is uniformly bounded from above, the anisotropic isoperimetric inequality would contradict the fact that
![]() $K_n$
is a minimizing sequence for
$K_n$
is a minimizing sequence for
![]() $\mathcal {J}_\Omega $
. Therefore,
$\mathcal {J}_\Omega $
. Therefore,
 $$ \begin{align*} h_{\hat{K}}(\Omega) |\hat{K}^\circ|^{\frac{1}{2}} & \leq \frac{\operatorname{\mathrm{Per}}_{\hat{K}}(\hat{C})}{|\hat{C}|}|\hat{K}^\circ|^{\frac{1}{2}} \\ & \leq \liminf_{n \to +\infty} \frac{\operatorname{\mathrm{Per}}_{K_n}(C_{K_n})}{|C_{K_n}|}|K_n^\circ|^{\frac{1}{2}} = \liminf_{n \to +\infty} h_{K_n}(\Omega)|K_n^\circ|^{\frac{1}{2}}, \end{align*} $$
$$ \begin{align*} h_{\hat{K}}(\Omega) |\hat{K}^\circ|^{\frac{1}{2}} & \leq \frac{\operatorname{\mathrm{Per}}_{\hat{K}}(\hat{C})}{|\hat{C}|}|\hat{K}^\circ|^{\frac{1}{2}} \\ & \leq \liminf_{n \to +\infty} \frac{\operatorname{\mathrm{Per}}_{K_n}(C_{K_n})}{|C_{K_n}|}|K_n^\circ|^{\frac{1}{2}} = \liminf_{n \to +\infty} h_{K_n}(\Omega)|K_n^\circ|^{\frac{1}{2}}, \end{align*} $$
which means
Since
![]() $\hat {K} \in \mathcal {K}_2$
and
$\hat {K} \in \mathcal {K}_2$
and
![]() $\{K_n\}_{n\in \mathbb {N}}$
is a minimizing sequence, the claim follows.
$\{K_n\}_{n\in \mathbb {N}}$
is a minimizing sequence, the claim follows.
4 Examples
In this section, we provide a few examples in order to highlight how the problem is far from being trivial. We have already made the useful observation that one can rewrite the functional
![]() $\mathcal {J}_\Omega [K]$
in terms of
$\mathcal {J}_\Omega [K]$
in terms of
![]() $\mathcal {F}_\Omega [K]$
as
$\mathcal {F}_\Omega [K]$
as
This easily allows to infer that there cannot be a set
![]() $K\in \mathcal {K}_2$
that always minimizes
$K\in \mathcal {K}_2$
that always minimizes
![]() $\mathcal {J}_\Omega [K]$
independently of the choice of
$\mathcal {J}_\Omega [K]$
independently of the choice of
![]() $\Omega $
.
$\Omega $
.
4.1
 $\Omega $
is a parallelogram
$\Omega $
is a parallelogram
Let T be an invertible affine transformation, and consider the parallelogram given by
![]() $T(Q)$
, where Q is the unit square in
$T(Q)$
, where Q is the unit square in
![]() $\mathbb {R}^2$
. By Proposition 2.2 and the fact that the Mahler volume is invariant with respect to invertible affine transformations,
$\mathbb {R}^2$
. By Proposition 2.2 and the fact that the Mahler volume is invariant with respect to invertible affine transformations,
for every
![]() $K \in \mathcal {K}_2$
. Moreover, as noticed in the introduction (see (1.10)),
$K \in \mathcal {K}_2$
. Moreover, as noticed in the introduction (see (1.10)),
![]() $T(Q)$
is the unique minimizer of
$T(Q)$
is the unique minimizer of
![]() $\mathcal {F}_{T(Q)}[K]$
. Hence,
$\mathcal {F}_{T(Q)}[K]$
. Hence,
for every
![]() $K \in \mathcal {K}_2$
, the strict inequality holding whenever
$K \in \mathcal {K}_2$
, the strict inequality holding whenever
![]() $K \neq T(Q)$
.
$K \neq T(Q)$
.
4.2
 $\Omega $
is a ball
$\Omega $
is a ball
Let
![]() $\Omega $
be the Euclidean ball B of unit radius. In this section, we show that the minimizing convex body
$\Omega $
be the Euclidean ball B of unit radius. In this section, we show that the minimizing convex body
![]() $K\in \mathcal {K}_2$
for
$K\in \mathcal {K}_2$
for
![]() $\mathcal {J}_B[K]$
can not be the ball itself. More in general, the square Q provides the lowest energy among all possible regular n-gons.
$\mathcal {J}_B[K]$
can not be the ball itself. More in general, the square Q provides the lowest energy among all possible regular n-gons.
Using (4.1), Proposition 2.2, and equality (1.10), we have as benchmark
We let
![]() $P^*_n$
be a regular n-gon, with
$P^*_n$
be a regular n-gon, with
![]() $n\ge 4$
even, circumscribed to B. With this choice, we have the following:
$n\ge 4$
even, circumscribed to B. With this choice, we have the following:
where the first one is a well known fact of Euclidean geometry, while the second equality comes from [Reference Böröczky, Makai, Meyer and Reisner2, Corollary 4]. We remark that the polar body of
![]() $P^*_n$
coincides with a rotation and a dilation by
$P^*_n$
coincides with a rotation and a dilation by
![]() of
of
![]() $P^*_n$
. In particular, we have the following information on the side length
$P^*_n$
. In particular, we have the following information on the side length
![]() $\operatorname {\mathrm {s}}(\cdot )$
, the apothem
$\operatorname {\mathrm {s}}(\cdot )$
, the apothem
![]() $\operatorname {\mathrm {a}}(\cdot )$
, and the circumradius
$\operatorname {\mathrm {a}}(\cdot )$
, and the circumradius
![]() $\operatorname {\mathrm {R}}(\cdot )$
of
$\operatorname {\mathrm {R}}(\cdot )$
of
![]() $P^*_n$
and its polar body
$P^*_n$
and its polar body
![]() $(P^*_n)^\circ $
:
$(P^*_n)^\circ $
:

that we shall use through the next computations.
Given the symmetry of B, any choice of K yields the same anisotropic constant of
![]() $T(K)$
, for any rotation
$T(K)$
, for any rotation
![]() $T\in \mathrm {SO}(2)$
. Hence, without loss of generality, we can suppose
$T\in \mathrm {SO}(2)$
. Hence, without loss of generality, we can suppose
![]() $P^*_n$
to be rotated in such a way that it has two sides parallel to the y-axis, and thus its polar body
$P^*_n$
to be rotated in such a way that it has two sides parallel to the y-axis, and thus its polar body
![]() $(P^*_n)^\circ $
has one diagonal on the x-axis (see Figure 1).
$(P^*_n)^\circ $
has one diagonal on the x-axis (see Figure 1).

Figure 1 On the left, the Wulff shape
![]() $P^*_n$
, and on the right, its polar body
$P^*_n$
, and on the right, its polar body
![]() $(P^*_n)^\circ $
inducing the metric
$(P^*_n)^\circ $
inducing the metric
![]() $\Phi _{P^*_n}^\circ $
, for
$\Phi _{P^*_n}^\circ $
, for
![]() $n=6$
. The unit radius disk appears dotted.
$n=6$
. The unit radius disk appears dotted.
By the symmetry of B, of
![]() $P^*_n$
and by Theorem 2.1, the boundary of the minimizer is made of n straight sides parallel to those of
$P^*_n$
and by Theorem 2.1, the boundary of the minimizer is made of n straight sides parallel to those of
![]() $P^*_n$
with endpoints on
$P^*_n$
with endpoints on
![]() $\partial B$
and n circular and symmetric arcs of
$\partial B$
and n circular and symmetric arcs of
![]() $\partial B$
, as in Figure 2. We consider the one-parameter family of competitors
$\partial B$
, as in Figure 2. We consider the one-parameter family of competitors
![]() $E_x$
that have this particular structure, being the parameter
$E_x$
that have this particular structure, being the parameter
![]() $x=x(n)$
half the length of one of the straight sides. Given the symmetric nature of our setting, we can divide the plane
$x=x(n)$
half the length of one of the straight sides. Given the symmetric nature of our setting, we can divide the plane
![]() $\mathbb {R}^2$
in
$\mathbb {R}^2$
in
![]() $2n$
symmetric circular sectors and compute the area and the anisotropic perimeter of these candidates in just one of these.
$2n$
symmetric circular sectors and compute the area and the anisotropic perimeter of these candidates in just one of these.

Figure 2 The shape of the Cheeger set in a sector of width
![]() w.r.t. the anisotropy given by the regular n-gon.
w.r.t. the anisotropy given by the regular n-gon.
The area in the sector
![]() $S_i$
is given by the area of a triangle with base
$S_i$
is given by the area of a triangle with base
![]() $\sqrt {1-x^2}$
and height x plus the area of a circular sector of radius
$\sqrt {1-x^2}$
and height x plus the area of a circular sector of radius
![]() $1$
and angle
$1$
and angle
, yielding
Concerning the perimeter, it is immediate that the Euclidean one is x plus
, but we should take into account the presence of the anisotropy. The straight side, of Euclidean length x, has constant normal given by the horizontal direction
![]() $e_1$
. By the choices we made (see (4.3)), the greatest
$e_1$
. By the choices we made (see (4.3)), the greatest
![]() $y\in \mathbb {R}_+$
such that
$y\in \mathbb {R}_+$
such that
![]() $ye_1 \in (P^*_n)^\circ $
is
$ye_1 \in (P^*_n)^\circ $
is
![]() $y=1$
, and thus
$y=1$
, and thus
![]() $\Phi _{P^*_n}^\circ (e_1)=1$
. Hence, this straight side has anisotropic perimeter equal to the Euclidean one. Concerning the circular arc, we can parameterize it as
$\Phi _{P^*_n}^\circ (e_1)=1$
. Hence, this straight side has anisotropic perimeter equal to the Euclidean one. Concerning the circular arc, we can parameterize it as
![]() $\gamma (\theta ) = (\cos \theta , \sin \theta )$
for
$\gamma (\theta ) = (\cos \theta , \sin \theta )$
for
, and thus
Hence, it is just a matter of computing the anisotropy
![]() $\Phi _{P^*_n}^\circ (\theta )$
. Given our initial assumptions, the point
$\Phi _{P^*_n}^\circ (\theta )$
. Given our initial assumptions, the point
![]() $e_1$
is a vertex of
$e_1$
is a vertex of
![]() $(P^*_n)^\circ $
, and the x-axis splits the interior angle with vertex in
$(P^*_n)^\circ $
, and the x-axis splits the interior angle with vertex in
![]() $e_1$
in two equal angles of width
$e_1$
in two equal angles of width
. Let
![]() $y\theta $
belong to the boundary
$y\theta $
belong to the boundary
![]() $(P^*_n)^\circ $
, for
$(P^*_n)^\circ $
, for
. Using the law of sines (see also Figure 3), we obtain the following equality:

and, since
![]() $\Phi _{P^*_n}^\circ (\theta ) = y^{-1}$
, we eventually get
$\Phi _{P^*_n}^\circ (\theta ) = y^{-1}$
, we eventually get
Hence,
 $$ \begin{align} \operatorname{\mathrm{Per}}_{P^*_n}(E_{x}) &= 2n\left( x + \frac{1}{\cos\left(\frac{\pi}{n} \right)} \int_{\arcsin(x)}^{\frac \pi n} \cos\left(\frac{\pi}{n} - \theta\right) \mathrm{d} \theta \right)\nonumber \\ &= 2n\left( x + \frac{\sin\left(\frac{\pi}{n} - \arcsin(x)\right)}{\cos\left(\frac{\pi}{n} \right)}\right). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Per}}_{P^*_n}(E_{x}) &= 2n\left( x + \frac{1}{\cos\left(\frac{\pi}{n} \right)} \int_{\arcsin(x)}^{\frac \pi n} \cos\left(\frac{\pi}{n} - \theta\right) \mathrm{d} \theta \right)\nonumber \\ &= 2n\left( x + \frac{\sin\left(\frac{\pi}{n} - \arcsin(x)\right)}{\cos\left(\frac{\pi}{n} \right)}\right). \end{align} $$
By (4.4) and (4.5), it follows that the Cheeger set
![]() $C_n$
of B, in the metric for which
$C_n$
of B, in the metric for which
![]() $P^*_n$
is the Wulff shape, coincides with
$P^*_n$
is the Wulff shape, coincides with
![]() $E_{x}$
, for the value
$E_{x}$
, for the value
![]() $\bar {x}_n$
that minimizes the ratio
$\bar {x}_n$
that minimizes the ratio
 $$ \begin{align} \frac{2}{\cos\left(\frac{\pi}{n} \right)} \frac{x \cos\left(\frac{\pi}{n} \right) + \sin\left(\frac{\pi}{n} - \arcsin(x)\right)}{ x \sqrt{1-x^2} + \frac{\pi}{n} - \arcsin(x)}\,. \end{align} $$
$$ \begin{align} \frac{2}{\cos\left(\frac{\pi}{n} \right)} \frac{x \cos\left(\frac{\pi}{n} \right) + \sin\left(\frac{\pi}{n} - \arcsin(x)\right)}{ x \sqrt{1-x^2} + \frac{\pi}{n} - \arcsin(x)}\,. \end{align} $$
Furthermore, recall that Theorem 2.1 states that the Cheeger set is the union of
![]() $\rho P^*_n$
, where
$\rho P^*_n$
, where
![]() $\rho $
is the inverse of the Cheeger constant. Thus, if
$\rho $
is the inverse of the Cheeger constant. Thus, if
![]() $\bar {x}_n$
is minimizing (4.6), we also have the following equality:
$\bar {x}_n$
is minimizing (4.6), we also have the following equality:
hence, the minimizing
![]() $\bar {x}_n$
is a solution of
$\bar {x}_n$
is a solution of
 $$\begin{align*}\frac{1}{x} \tan\left(\frac \pi n\right)= \frac{2}{\cos\left(\frac{\pi}{n} \right)} \frac{x \cos\left(\frac{\pi}{n} \right) + \sin\left(\frac{\pi}{n} - \arcsin(x)\right)}{ x \sqrt{1-x^2} + \frac{\pi}{n} - \arcsin(x)} \end{align*}$$
$$\begin{align*}\frac{1}{x} \tan\left(\frac \pi n\right)= \frac{2}{\cos\left(\frac{\pi}{n} \right)} \frac{x \cos\left(\frac{\pi}{n} \right) + \sin\left(\frac{\pi}{n} - \arcsin(x)\right)}{ x \sqrt{1-x^2} + \frac{\pi}{n} - \arcsin(x)} \end{align*}$$
and
At this point, use the trigonometric identity
to simplify the identity into
 $$\begin{align*}\frac{1}{x} = \frac{2\sqrt{1-x^2}}{ x \sqrt{1-x^2} + \frac{\pi}{n} - \arcsin(x)}, \end{align*}$$
$$\begin{align*}\frac{1}{x} = \frac{2\sqrt{1-x^2}}{ x \sqrt{1-x^2} + \frac{\pi}{n} - \arcsin(x)}, \end{align*}$$
and hence
![]() $\bar {x}_n$
solves
$\bar {x}_n$
solves
Since the function on the LHS is increasing in x, there exists a unique solution, and the function
![]() $n \mapsto \bar {x}_n$
is decreasing, so that the maximum value of
$n \mapsto \bar {x}_n$
is decreasing, so that the maximum value of
![]() $\bar {x}_n$
is attained for
$\bar {x}_n$
is attained for
![]() $n=4$
. Unfortunately this equation cannot be solved explicitly for x, but its unique solution for each n can be numerically computed: a plot of the map
$n=4$
. Unfortunately this equation cannot be solved explicitly for x, but its unique solution for each n can be numerically computed: a plot of the map
![]() $n \mapsto \bar {x}_n$
is shown in Figure 4(a), and some values are collected in Table 1.
$n \mapsto \bar {x}_n$
is shown in Figure 4(a), and some values are collected in Table 1.

Figure 3 Close up of the unit ball in the metric
![]() $\Phi _{P^*_n}^\circ $
. The dots individuate the sectors of the Euclidean unit ball B with angles
$\Phi _{P^*_n}^\circ $
. The dots individuate the sectors of the Euclidean unit ball B with angles
![]() and
and
![]() .
.

Figure 4 Graphs of
![]() $\bar {x}_n$
(LHS) and of
$\bar {x}_n$
(LHS) and of
![]() $\mathcal {J}_B[P^*_n]$
(RHS).
$\mathcal {J}_B[P^*_n]$
(RHS).
Table 1 Values of the minimizing half-side
![]() $\bar {x}_n$
and of the functional
$\bar {x}_n$
and of the functional
![]() $\mathcal {J}_B[P^*_n]$
for some choices of n.
$\mathcal {J}_B[P^*_n]$
for some choices of n.

The lack of an explicit expression for
![]() $\bar {x}_n$
prevents us from having an explicit value of
$\bar {x}_n$
prevents us from having an explicit value of
![]() $ \mathcal {J}_{B}[P^*_n]$
. Nevertheless, we can easily give an upper and a lower bound to
$ \mathcal {J}_{B}[P^*_n]$
. Nevertheless, we can easily give an upper and a lower bound to
![]() $\bar {x}_n$
. On the one hand, as a consequence of the isoperimetric inequality, we can estimate
$\bar {x}_n$
. On the one hand, as a consequence of the isoperimetric inequality, we can estimate
![]() $h_{P^*_n}(B)$
from below by
$h_{P^*_n}(B)$
from below by
![]() $h_{P^*_n}(\rho P^*_n)$
, where
$h_{P^*_n}(\rho P^*_n)$
, where
![]() $\rho $
is such that
$\rho $
is such that
![]() $|\rho P^*_n| = |B|=\pi $
. This gives
$|\rho P^*_n| = |B|=\pi $
. This gives
By the relations in (4.2), we have
and solving for
![]() $\rho $
and plugging in (4.9) gives
$\rho $
and plugging in (4.9) gives
 $$\begin{align*}\bar{x}_n \le \frac{\sqrt{\pi}}{2} \sqrt{\frac{\tan\left(\frac \pi n\right)}{n}}\,. \end{align*}$$
$$\begin{align*}\bar{x}_n \le \frac{\sqrt{\pi}}{2} \sqrt{\frac{\tan\left(\frac \pi n\right)}{n}}\,. \end{align*}$$
On the other hand, using as competitor
, that is the greatest Wulff shape contained in B, by definition of K-Cheeger constant, we obtain, as a lower bound,
 $$ \begin{align*} \frac{1}{\bar{x}_n} \tan\left(\frac \pi n\right) = h_{P^*_n}(B) &\le \frac{\operatorname{\mathrm{Per}}_{P^*_n}(\cos\left(\frac \pi n\right) P^*_n)}{|\cos\left(\frac \pi n\right) P^*_n|} \\ &= \frac{1}{\cos \left(\frac \pi n\right)} \frac{\operatorname{\mathrm{Per}}_{P^*_n}(P^*_n)}{|P^*_n|} = \frac{2}{\cos \left(\frac \pi n\right)}\,. \end{align*} $$
$$ \begin{align*} \frac{1}{\bar{x}_n} \tan\left(\frac \pi n\right) = h_{P^*_n}(B) &\le \frac{\operatorname{\mathrm{Per}}_{P^*_n}(\cos\left(\frac \pi n\right) P^*_n)}{|\cos\left(\frac \pi n\right) P^*_n|} \\ &= \frac{1}{\cos \left(\frac \pi n\right)} \frac{\operatorname{\mathrm{Per}}_{P^*_n}(P^*_n)}{|P^*_n|} = \frac{2}{\cos \left(\frac \pi n\right)}\,. \end{align*} $$
Putting these two inequalities together, we get
 $$ \begin{align} \frac{1}{2} \sin \left(\frac \pi n\right) \le \bar{x}_n \le \frac{\sqrt{\pi}}{2} \sqrt{\frac{\tan\left(\frac \pi n\right)}{n}}\,. \end{align} $$
$$ \begin{align} \frac{1}{2} \sin \left(\frac \pi n\right) \le \bar{x}_n \le \frac{\sqrt{\pi}}{2} \sqrt{\frac{\tan\left(\frac \pi n\right)}{n}}\,. \end{align} $$
This is enough to prove that
![]() $\mathcal {J}_B[P^*_n]$
achieves its minimum on
$\mathcal {J}_B[P^*_n]$
achieves its minimum on
![]() $P^*_4$
. Indeed, recalling (4.7) and (4.2), one has
$P^*_4$
. Indeed, recalling (4.7) and (4.2), one has
Using the bounds in (4.10), one has
 $$\begin{align*}\frac{2n}{\sqrt{\pi}} \sin\left(\frac{\pi}{n} \right)\le \mathcal{J}_{B}[P^*_n] \le 2 \sqrt{n \tan\left(\frac \pi n\right)}\,. \end{align*}$$
$$\begin{align*}\frac{2n}{\sqrt{\pi}} \sin\left(\frac{\pi}{n} \right)\le \mathcal{J}_{B}[P^*_n] \le 2 \sqrt{n \tan\left(\frac \pi n\right)}\,. \end{align*}$$
Both the LHS and the RHS converge to
![]() $2\sqrt {\pi }$
, and, in particular, the LHS is greater than
$2\sqrt {\pi }$
, and, in particular, the LHS is greater than
![]() $\mathcal {J}_{B}[P^*_4]$
as soon as
$\mathcal {J}_{B}[P^*_4]$
as soon as
![]() $n\ge 12$
. In order to conclude, it is enough to check a finite number of values
$n\ge 12$
. In order to conclude, it is enough to check a finite number of values
![]() $\mathcal {J}_{B}[P^*_n]$
, corresponding to
$\mathcal {J}_{B}[P^*_n]$
, corresponding to
![]() $n=4, 6, 8, 10$
. These, along with some other values, numerically obtained, are reported in Table 1, along with the value of
$n=4, 6, 8, 10$
. These, along with some other values, numerically obtained, are reported in Table 1, along with the value of
![]() $\bar {x}_n$
minimizing (4.6) subject to the constraint (4.10). Graphs depicting the behavior of
$\bar {x}_n$
minimizing (4.6) subject to the constraint (4.10). Graphs depicting the behavior of
![]() $\bar {x}_n$
and
$\bar {x}_n$
and
![]() $\mathcal {J}_{B}[P^*_n]$
for the first
$\mathcal {J}_{B}[P^*_n]$
for the first
![]() $100$
even numbers
$100$
even numbers
![]() $n\ge 4$
are shown in Figures 4(a),4(b). We conjecture that
$n\ge 4$
are shown in Figures 4(a),4(b). We conjecture that
![]() $\mathcal {J}_{B}[P^*_n]$
is actually increasing in n.
$\mathcal {J}_{B}[P^*_n]$
is actually increasing in n.
5 Final remarks and open questions
In this paper, we initiated the study of optimization of anisotropic shape functionals with respect to the anisotropy. We proved that the minimization problem for the functional
![]() $\mathcal {J}_\Omega $
is well posed, and we obtained some partial results in the case when
$\mathcal {J}_\Omega $
is well posed, and we obtained some partial results in the case when
![]() $\Omega $
is a ball. We are left with several open questions.
$\Omega $
is a ball. We are left with several open questions.
-
• Is it possible to show existence of minimizers in the N-dimensional case? The difficulty lies in the fact that, apart from the planar case, there is no obvious characterization of K-Cheeger sets, which is a key ingredient of the proof of Proposition 3.1.
-
• If
 $\Omega =B$
, is it true that
$\Omega =B$
, is it true that
 $\mathcal {J}_B[P^*_n] \le \mathcal {J}_B[P]$
for any polygon with sides
$\mathcal {J}_B[P^*_n] \le \mathcal {J}_B[P]$
for any polygon with sides
 $n$
? While this assertion might seem reasonable, we need to observe, bearing in mind equation (1.11), that the Mahler volume V is actually maximized, among all polygons with n sides, by the regular one (see also [Reference Meyer and Reisner18]).
$n$
? While this assertion might seem reasonable, we need to observe, bearing in mind equation (1.11), that the Mahler volume V is actually maximized, among all polygons with n sides, by the regular one (see also [Reference Meyer and Reisner18]).
The functional that has been considered in this paper involves only purely geometrical quantities. In the literature, several other functionals, involving anisotropic differential operators, have been investigated; we can mention, among others, the first eigenvalue of the anisotropic p-Laplacian [Reference Kawohl and Novaga11], which is defined, for
![]() $p \in (1,+\infty )$
, as
$p \in (1,+\infty )$
, as
 $$\begin{align*}\lambda_p^K(\Omega) := \inf_{u \in W^{1,p}_0(\Omega)} \frac{\int_\Omega (\Phi^\circ(|\nabla u|))^p}{\int_\Omega |u|^p}.\end{align*}$$
$$\begin{align*}\lambda_p^K(\Omega) := \inf_{u \in W^{1,p}_0(\Omega)} \frac{\int_\Omega (\Phi^\circ(|\nabla u|))^p}{\int_\Omega |u|^p}.\end{align*}$$
It would be interesting to carry a similar analysis for the shape optimization problem
However, this problem is considerably more difficult than the one considered in the present work, since nongeometrical quantities are involved. We remark that the results proved here, combined with some well known inequalities between the first eigenvalue of the anisotropic Dirichlet p-Laplacian and the anisotropic Cheeger constant allow us to say something in the two-dimensional case. Namely, we have the following.
Remark 5.1. The K-Cheeger constant provides a lower bound to the first eigenvalue of the anisotropic Dirichlet p-Laplacian
![]() $\lambda ^K_p(\Omega )$
(Cheeger’s inequality; see [Reference Kawohl and Novaga11]). Then, from Proposition 3.1, it follows that, for the scaling invariant functional
$\lambda ^K_p(\Omega )$
(Cheeger’s inequality; see [Reference Kawohl and Novaga11]). Then, from Proposition 3.1, it follows that, for the scaling invariant functional
![]() ${K \mapsto \lambda ^K_p(\Omega ) |K^\circ |^{\frac {p}{2}}}$
, has infinite supremum in
${K \mapsto \lambda ^K_p(\Omega ) |K^\circ |^{\frac {p}{2}}}$
, has infinite supremum in
![]() $\mathcal {K}_2$
.
$\mathcal {K}_2$
.
Remark 5.2. Besides the lower bound to
![]() $\lambda ^K_p(\Omega )$
provided by Cheeger’s inequality [Reference Kawohl and Novaga11], the K-Cheeger constant also provides an upper bound to
$\lambda ^K_p(\Omega )$
provided by Cheeger’s inequality [Reference Kawohl and Novaga11], the K-Cheeger constant also provides an upper bound to
![]() $\lambda ^K_p(\Omega )$
, known as Buser’s inequality or reverse Cheeger’s inequality (refer to [Reference Brasco3, Reference Della Pietra, di Blasio and Gavitone6, Reference Ftouhi7, Reference Parini23]). Hence, from Proposition 3.3, it follows that the shape functional
$\lambda ^K_p(\Omega )$
, known as Buser’s inequality or reverse Cheeger’s inequality (refer to [Reference Brasco3, Reference Della Pietra, di Blasio and Gavitone6, Reference Ftouhi7, Reference Parini23]). Hence, from Proposition 3.3, it follows that the shape functional
![]() $K\mapsto \lambda ^K_p(\Omega ) |K^\circ |^{\frac {p}{2}}$
has nonzero, finite infimum in
$K\mapsto \lambda ^K_p(\Omega ) |K^\circ |^{\frac {p}{2}}$
has nonzero, finite infimum in
![]() $\mathcal {K}_2$
.
$\mathcal {K}_2$
.