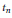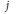Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Berndt, Bruce C.
Chan, Heng Huat
Kang, Soon-Yi
and
Zhang, Liang-Cheng
2002.
A certain quotient of eta-functions found in Ramanujan’s lost notebook.
Pacific Journal of Mathematics,
Vol. 202,
Issue. 2,
p.
267.
Chan, Heng Huat
Tan, Victor
and
Gee, Alice
2003.
Cubic singular moduli, Ramanujan’s class invariants λnand the explicit Shimura Reciprocity Law.
Pacific Journal of Mathematics,
Vol. 208,
Issue. 1,
p.
23.
Baruah, Nayandeep Deka
Berndt, Bruce C.
and
Chan, Heng Huat
2009.
Ramanujan's Series for 1/π: A Survey.
The American Mathematical Monthly,
Vol. 116,
Issue. 7,
p.
567.
Konstantinou, Elisavet
and
Kontogeorgis, Aristides
2009.
Computing Polynomials of the Ramanujan tn Class Invariants.
Canadian Mathematical Bulletin,
Vol. 52,
Issue. 4,
p.
583.
Konstantinou, Elisavet
and
Kontogeorgis, Aristides
2010.
Ramanujan’s class invariants and their use in elliptic curve cryptography.
Computers & Mathematics with Applications,
Vol. 59,
Issue. 8,
p.
2901.
Enge, Andreas
and
Sutherland, Andrew V.
2010.
Algorithmic Number Theory.
Vol. 6197,
Issue. ,
p.
142.
Bostan, A.
Boukraa, S.
Hassani, S.
Maillard, J.-M.
Weil, J.-A.
Zenine, N.
Abarenkova, N.
and
Kerner, Richard
2010.
Renormalization, Isogenies, and Rational Symmetriesof Differential Equations.
Advances in Mathematical Physics,
Vol. 2010,
Issue. 1,
Bostan, A
Boukraa, S
Hassani, S
van Hoeij, M
Maillard, J-M
Weil, J-A
and
Zenine, N
2011.
The Ising model: from elliptic curves to modular forms and Calabi–Yau equations.
Journal of Physics A: Mathematical and Theoretical,
Vol. 44,
Issue. 4,
p.
045204.
Bagis, N.D.
and
Glasser, M.L.
2012.
Conjectures on the evaluation of alternative modular bases and formulas approximating 1/π.
Journal of Number Theory,
Vol. 132,
Issue. 10,
p.
2353.
KONSTANTINOU, ELISAVET
and
KONTOGEORGIS, ARISTIDES
2012.
RAMANUJAN INVARIANTS FOR DISCRIMINANTS CONGRUENT TO 5 (mod 24).
International Journal of Number Theory,
Vol. 08,
Issue. 01,
p.
265.
Chan, Heng Huat
Konstantinou, Elisavet
Kontogeorgis, Aristides
and
Tan, Chik How
2012.
What is your “birthday elliptic curve”?.
Finite Fields and Their Applications,
Vol. 18,
Issue. 6,
p.
1232.
Bagis, N.D.
and
Glasser, M.L.
2013.
Ramanujan type1/πapproximation formulas.
Journal of Number Theory,
Vol. 133,
Issue. 10,
p.
3453.
2013.
Primes of the Formx2+ ny2.
p.
343.
Hu, Jian Jun
2014.
Constructing Elliptic Curves over Ramanujan's Class Invariants.
Advanced Materials Research,
Vol. 915-916,
Issue. ,
p.
1336.
Konstantinou, Elisavet
and
Kontogeorgis, Aristides
2015.
Computation, Cryptography, and Network Security.
p.
299.
Hu, Xiaowen
2015.
Localized Standard Versus Reduced Formula and Genus 1 Local Gromov–Witten Invariants.
International Mathematics Research Notices,
Vol. 2015,
Issue. 20,
p.
9921.
Paek, Dae Hyun
and
Yi, Jinhee
2015.
ON EVALUATIONS OF THE MODULAR j-INVARIANT BY MODULAR EQUATIONS OF DEGREE 2.
Bulletin of the Korean Mathematical Society,
Vol. 52,
Issue. 1,
p.
263.
Baruah, Nayandeep Deka
Berndt, Bruce C.
and
Chan, Heng Huat
2016.
Pi: The Next Generation.
p.
303.
Abdelaziz, Y
and
Maillard, J-M
2017.
Modular forms, Schwarzian conditions, and symmetries of differential equations in physics.
Journal of Physics A: Mathematical and Theoretical,
Vol. 50,
Issue. 21,
p.
215203.
Pazuki, Fabien
2019.
Modular invariants and isogenies.
International Journal of Number Theory,
Vol. 15,
Issue. 03,
p.
569.